几何最值问题新考
2010-11-24金陵中学河西分校江苏南京210019
● (金陵中学河西分校 江苏南京 210019)
在各种版本的数学教材中,我们都会看到下面一道经典的几何作图题:
条件如图1,A,B是直线l同旁的2个定点.
问题在直线l上确定一点P,使得PA+PB的值最小.
方法作点A关于直线l的对称点A′,连结A′B交直线l于点P,则PA+PB=A′B的值最小.
该作图题的实质是已知2个定点,确定1个动点,使动点到2个定点的距离之和最短,它的典型应用是解决线段和的最小值问题.纵观近几年中考试题中的几何最值问题,绝大多数都是这一模型的变式或拓展应用,本文探究的是不能用此类模型解决的另类最值问题,供读者参考.

图1
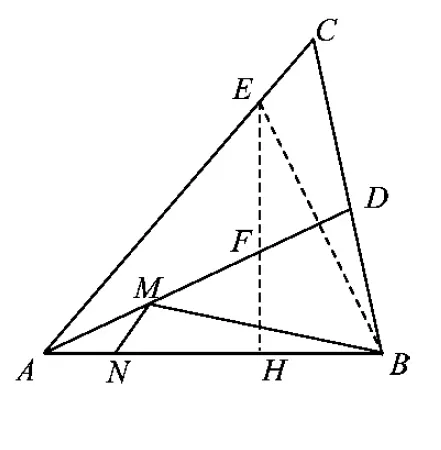
图2
1 双动点型线段和的最小值

(2009年陕西省数学中考试题)

例2定义一种变换:平移抛物线F1得到抛物线F2,使F2经过F1的顶点A.设F2的对称轴分别交F1,F2于点D,B,点C是点A关于直线BD的对称点.
(1)如图3,若F1:y=x2,经过变换后,得到F2:y=x2+bx,点C的坐标为(2,0),则
①b的值等于________;
②四边形ABCD为
( )
A.平行四边形 B.矩形
C.菱形 D.正方形
(2)如图4,若F1:y=ax2+c,经过变换后,点B的坐标为(2,c-1),求△ABD的面积.

(2009年浙江省绍兴市数学中考试题)

图3

图4
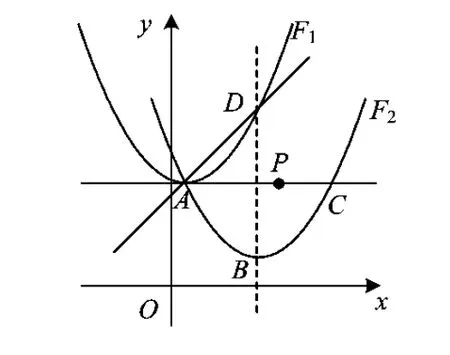
图5
图6
分析(1)-2;D.
(2)S△ABD=2.
(3)①当点C在点A的右侧时(如图6).设AC与BD交于点N,则

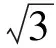
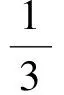
于是
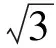
NB=ND=1.
由点A与点C关于直线BD对称,得
AC⊥DB,且AN=NC,
于是四边形ABCD是菱形,点B与点D关于直线AC对称,从而PD=PB.作PH⊥AD交AD于点H,则
PD+PH=PB+PH.
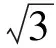

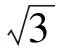
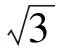
评析与常规求线段和的最小值不同,例1中有2个动点,例2中的第(3)小题涉及到2种距离,其实质是作PH⊥AD于点H转化为求“PD+PH”的最小值,点P,H也是2个动点,这类“双动点型”线段和的最小值问题,可先用轴对称性找到对称点,再作垂线段用“垂线段最短”求解.
在运用该系统的过程最后,车辆进场前,需在项目部安全环保部门办理台账登记手续(三证齐全),手续齐全后发项目部自编号,由设备物资科进行电子标签的录入信息工作,录入完成后装料,装料到达自动称重系统后看指示灯(红绿灯),当绿灯亮时,车辆行驶到电子标签扫描区域,扫描成功后道闸打开,车辆进入称台中间(此时红外线已扫描)不用停车方可称重记录,记录成功后语音提示称重保存成功,显示屏显示称重数据,道闸打开车辆通过称重完毕。

图7
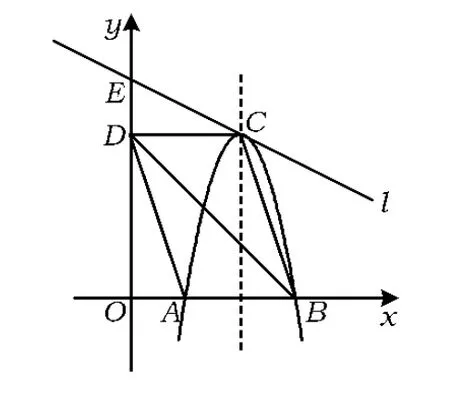
图8
2 线段和的最大值问题
例3如图8,在平面直角坐标系中,四边形ABCD是平行四边形,边AB在x轴上,且AB=6,D(0,9),以点C为顶点的抛物线经过点A,B,直线l过点C,交y轴于点E(0,12).
(1)求抛物线的解析式.
(2)若抛物线的顶点C沿直线l向上移动,当抛物线经过点D时,求抛物线的解析式和点A,C间的抛物线弧扫过的面积.
(3)P是线段BD上的动点,连结CP,点B,D到直线CP的距离之和是否存在最大值?若存在,请求出其最大值和此时点P的坐标;若不存在,请说明理由.
(2009年贵州省铜仁地区数学中考试题)
分析(1)抛物线的解析式为
y=-(x-6)2+9.
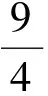
即
于是


图9
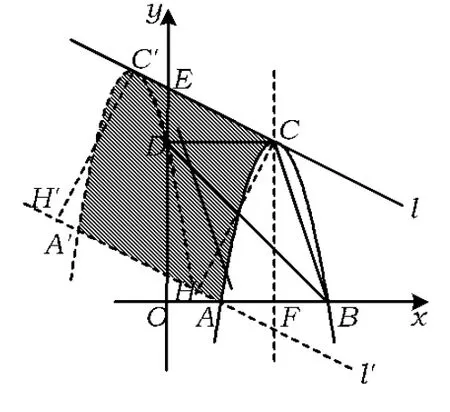
图10
当m=4时,如图10,抛物线的解析式为
y=-(x-6+2×4)2+9+4,
即
y=-(x+2)2+13,
于是

(3)存在.由“点到直线的距离最短”可知,点B,D到直线CP的距离之和小于或等于BP+PD=BD,即当直线CP⊥BD时,点B,D到直线CP的距离之和取得最大值,即等于线段BD的长度,如图11.过点P作PM⊥CD于点M.由
OB=OD=9,∠BOD=90°,
得△BOD是等腰直角三角形,于是
∠ODB=45°,∠BDC=45°,
从而△PCD是等腰直角三角形.又由PM⊥CD,得

于是9-3=6,因而点P的坐标为(3,6).
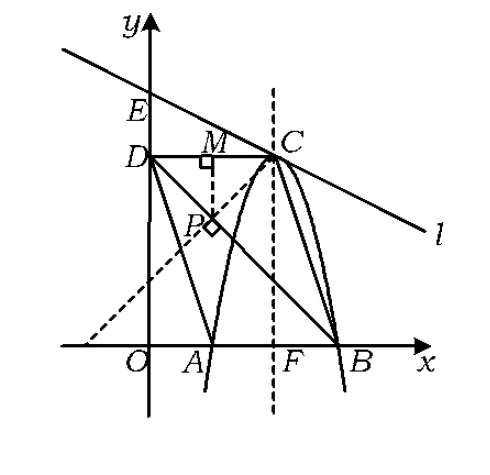
图11

图12
例4如图12,在平面直角坐标系中,开口向上的抛物线与x轴交于点A,B,D为抛物线的顶点,O为坐标原点.若OA,OB(OA (1)求抛物线对应的二次函数解析式; (2)过点A作AC⊥AD交抛物线于点C,求点C的坐标; (3)在第(2)小题的条件下,过点A任作直线l交线段CD于点P,点C,D到直线l的距离分别为d1,d2,试求d1+d2的最大值. (2009年四川省乐山市数学中考试题) 分析(1)抛物线对应的二次函数解析式为 (2)点C的坐标为(5,6). (3)由第(2)小题知 于是 过点A作AM⊥DC于点M(如图13).由 得 又由 S△ADC=S△APD+S△APC, 得 从而 评析例4也可用例3的解法求解.因为 d1+d2≤DP+PC=CD, 图13 图14 (1)求点A,B的坐标; (2)若点P是x轴上任意一点,求证: PA-PB≤AB; (3)当PA-PB最大时,求点P的坐标. (2009年广西贺州市数学中考试题) 分析(1)A(-2,3),B(0,2). (2)当点P是AB的延长线与x轴的交点时,PA-PB=AB. 当点P在x轴上又异于AB的延长线与x轴的交点时,在△PAB中,PA-PB 综上所述,PA-PB≤AB. (3)作直线AB交x轴于点P.由第(2)小题可知:当PA-PB最大时,点P是所求的点.作AH⊥OP于点H.由BO⊥OP,得 △BOP∽△AHP, 于是 由第(1)小题可知 AH=3,OH=2,OB=2, 于是OP=4,故P(4,0). 图15 (1)求该抛物线的解析式; (2)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标; (3)在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标. (2009年四川省眉山市数学中考试题) 分析(1)该抛物线的解析式为 k=-1,b=1, 于是直线AB的解析式为y=-x+1.由 得 评析例1的第(2)小题通过一个简单的几何证明题揭示了解决问题的方法:一般地,线段差的最大值问题可利用“三角形两边之差小于第三边”转化成3个点在同一条直线上时来处理.在“动”转化为“静”的过程中,对学生的思维能力提出了较高的要求,对学生利用数形结合思想以及转化策略的能力进行了有效考查. 新课改实施以来的数学中考,最值问题成为十分热门的题型,在压轴题中占据一席之地.试题常以几何图形或平面直角坐标系为载体,与其他知识综合,形成背景新颖、创意独特的一类问题,考查学生在图形的运动变化过程中探究几何的数量关系和位置关系的能力,体现新课程对几何探究、推理能力的要求.

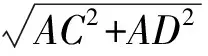








3 线段差的最大值问题