探究高考试题 重视引申教学

● (苏苑高级中学 江苏苏州 215128)

波利亚认为中学数学教育的根本宗旨是“教会年轻人思考”.在当前的教育模式下，每一位教师都应该认真研究高考试题，不仅研究试题如何解决，还应研究试题的背景、与课本知识的联系.因为有很多题目本身是出自课本题目或进行了适当的改编.在这些内容已经基本研究清楚的情况下，还应该研究解决题目的方法和思想，对该题的知识和方法的延伸，以及改变题目某些条件而出现的新题，更为重要的是教会学生如何思考.

针对近几年江苏省数学高考部分试题，笔者做了一些引申，在《数学通讯》2006年第11期上发表了对2006年江苏省数学高考试题第21题的引申的文章，并在平时课堂教学中加以实践，这对课堂教学有一定的帮助.波利亚说：“当你找到第一个蘑菇后，要环顾四周，因为它们总是成堆生长的”.在解题教学中，解题后的反思不单是简单的回顾或检验，而应引导学生仔细分析问题的结构特点，寻找各科知识的交叉点，总结、理清、概括思路，做到举一反三、触类旁通，以培养学生的发散思维和知识迁移能力，并引导学生对命题进行条件弱化和结论加强、推广、引申等的反思.

1 从合情推理的角度对试题的知识覆盖进行引申

合情推理是波利亚的“启发法”中的一个推理模式,归纳推理和类比推理统称为合情推理.归纳推理就是从具体到一般的推理，对试题的归纳推理就是将条件弱化、一般性处理后的一种推理，譬如归纳出数列的通项公式等.类比推理就是将问题类比到具有某些共同属性的知识上去而得到的一些推理结果，譬如将等差数列问题类比到等比数列问题，平面几何问题类比到立体几何问题等.此类问题的引申能提高课堂教学和学生学习知识的深度和广度.

例1设数列{an},{bn},{cn}满足：bn=an-an+2,cn=an+2an+1+3n+2(n=1,2,3,…),证明:{an}为等差数列的充分必要条件是{cn}为等差数列,且bn≤bn+1(n=1,2,3,…).

(2006年江苏省数学高考试题)

引申1设数列{an},{bn},{cn}满足:bn=an-an+2,cn=an+2an+1+3an+2+…+(k+1)an+k(n=1,2,3,…;k∈N*),证明:{an}为等差数列的充分必要条件是{cn}为等差数列,且bn≤bn+1(n=1,2,3,…).

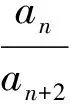
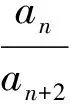
2 从数学思想方法的角度对试题的解法进行引申

中学数学思想方法有许多，主要有分类讨论思想、数形结合思想、函数方程思想和等价转化思想.在教学中,若能让学生真正领会这些思想,这将对高考解题有很大的帮助.

譬如,许多数学问题有“代数和几何”的双重背景，在解决时可以从这2个角度去思考，可以锻炼学生的抽象思维与形象思维.

图1

江苏2009高考数学试题第18题：

例2如图1,在平面直角坐标系xOy中，已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.

(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l1和l2，它们分别与圆C1和C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求所有满足条件的点P的坐标.

除了试题给出的答案外，还可以用数形结合思想解决问题.

由上可见，此题用数形结合思想有效地化解了复杂的代数运算，在教学过程中不妨经常引导学生将代数方法与几何方法转换使用.

3 从弱化命题条件的角度对试题的结论进行引申

一个命题有条件和结论这2个部分，如果将条件弱化，从具体数据引申为一般情形，那么就改变了命题的题设，从而对结论产生影响.有时结论仍然成立，有时结论不成立，这就需要我们去判断和证明.如此训练，一方面可以让学生认清某类知识和方法的本质;另一方面还能提高学生的自主探索能力.

对2009年江苏省数学高考试题第18题还可进行如下引申：

引申4若平面内有2个不重合的圆C1,C2，在平面内是否存在点P，使得过点P的无穷多对互相垂直的直线l1和l2，分别与圆C1和C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等.如果存在，求出点P；如果不存在，请说明理由.

分析选择用代数方法运算.

建立平面直角坐标系，使得圆C1,C2的圆心分别为(-a，0)和(a，0).设圆C1,C2的半径分别为r1,r2,点P的坐标为(m,n),直线l1和l2的方程分别为

即

由题意可得

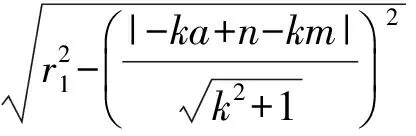
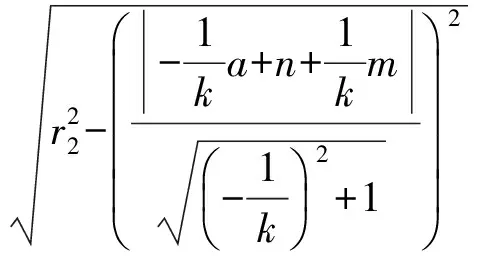
化简得

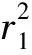
4nmk+[n2-(m-a)2],

此关于k的方程有无穷多解.由

解得

显然第2组解不符题意，舍去.第1组解表示：要有满足题意的解，两圆半径必须相同，点P必须在两圆心连线段的垂直平分线上，且点P到此垂直平分线的距离等于两圆心连线段距离的一半.在这种情形下，点P有且只有2个，这2个点与两圆心正好围成一个正方形.如果不满足上述情形，那么这样的点P不存在.

引申5若平面内有2个不重合的圆C1,C2，在平面内是否存在点P，使得过点P的无穷多对夹角恒定的直线l1和l2，它们分别与圆C1和C2相交，且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等.如果存在，求出点P；如果不存在，请说明理由.

分析选择用几何方法说理.

当2个圆半径相同时，当直线l1经过圆心C1，直线l2经过圆心C2时，它们被圆截得的弦长相等，都为圆的直径，点P应在线段C1C2的垂直平分线l上.因为l1,l2夹角恒定，所以点P也在以线段C1C2为一条弦且其所对的圆周角恒定的2段圆弧C上，即点P是直线l与C的交点，这样的点P有且只有2个(点A，B).当l1,l2绕点P旋转至l1′,l2′时，各自旋转的角度相同，C1到l1′的距离与C2到l2′距离相等.由垂径定理可知，直线l1′被圆C1截得的弦长与直线l2′被圆C2截得的弦长相等.因此满足条件的点P就是A，B，此时四边形AC1BC2为菱形，利用解析几何知识，写出线段C1C2的垂直平分线l的方程和以线段C1C2为一条弦且其所对的圆周角恒定的2段圆弧C的方程通过解方程组，不难求出点A，B的坐标.

当2个圆半径不相同时，可以证明这样的点P不存在.

上述试题的引申揭示了知识的内在联系和本质特征(内涵与外延)：此类问题可以运用代数的运算来解决几何问题，也可以从圆的几何性质来直接研究几何问题.

4 从与课本联系的角度对试题的源头进行引申

在注重基础知识和方法的基础上，如果能够对课本内容进行进一步研究和引申，有助于学生理解问题的本质，提高学生研究问题的能力.例如2008年江苏省数学高考试题第13题：

这2个问题的本质是相同的，如果引申为一般情形，那么即可得到：

若到2个定点的距离之比为常数(不为1)的点的轨迹是一个圆，则称之为阿波罗尼斯圆.

抓住这个本质后，例3就不难解决了.

[1] 中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2005.

[2] 高德龙.2006年一道高考题的引申[J].数学通讯,2006(11)：11-12