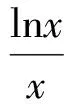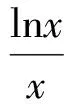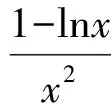用分离参数法求取值范围
2010-11-24任丘市第一中学河北任丘062550
● (任丘市第一中学 河北任丘 062550)
求参数的取值范围问题是中学数学的重点,也是一个难点.学生在解答此类问题时往往会因分类不恰当或讨论不全面而出现错误.为迅速、准确地处理一类求参数取值范围问题,给出一种方法——分离参数法.
下面举例说明如何用分离参数法求取值范围.
1 分离参数,利用三角函数的有界性求取值范围
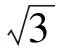
解已知方程整理得
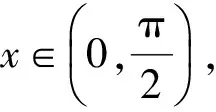
因此原方程有2个实根等价于
即
于是
-1 故实数m的取值范围为(-1,2]. 例2不等式ax2+a|x|+a-1<0对任意实数x都成立,求实数a的取值范围. 解由ax2+a|x|+a-1<0,得 因为 得 所以 故a≤0,即实数a的取值范围为(-∞,0]. 例3已知函数f(x)=lg(ax+a-x-m)(a>0,且a≠1)的定义域为实数集R,求实数m的取值范围. 解先分离参数k,得 由x∈(0,3],得 同理,分离m得 因此 f(3)≤f(x) 即 于是 例5若方程x2-2ax-a+2=0有正根,求实数a的取值范围. 分析方程有正根包含3种情形:两根均为正,一正一零,一正一负.若直接按根的分布讨论,则比较复杂.可先分离参数,再结合换元法求解,则简洁得多. 分离参数a,得 设t=2x+1(t>1),则 因此 解先分离a.由题意得 因此 因此 a<3. 例7若lnx-(k+1)x<0在(0,+∞)上恒成立,求实数k的取值范围. 解分离k得 (k+1)x>lnx, 即 解方程f′(x)=0,得x=1.又当x∈(0,1)时,f′(x)>0;当x∈(1,+∞)时,f′(x)<0.于是 f(x)max=f(1)=0, 解得 k+1>0, 即k>-1,故实数k的取值范围为(-1,+∞). 由以上几例可以看出,在一个方程、函数或不等式中,若涉及到求参数取值范围的问题,则可先考虑能否将它作适当变形,将所求参数分离出来,通过考察函数单调性、有界性,不等式性质,或结合换元法、导数等转化成求含该参数一端值域或最值的问题,这就是分离参数法.这种方法集化归与转化思想、整体与换元思想于一身,可尽量避免对参数的讨论,在求参数范围这个热点问题中有着独特的解题优势.2 分离参数,用代数式的性质求取值范围
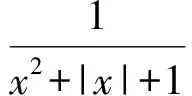
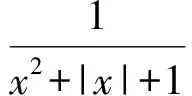
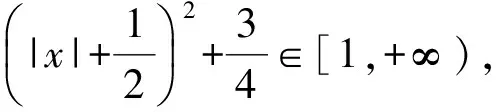
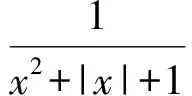
3 分离参数,用均值不等式求取值范围
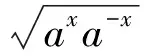
4 分离参数,用常见函数的单调性求范围
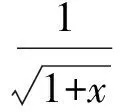

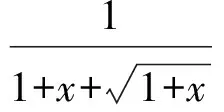
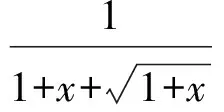
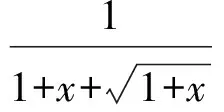
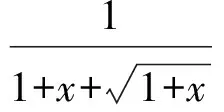
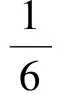
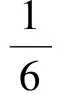
5 分离参数,用换元法求取值范围
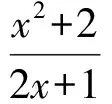

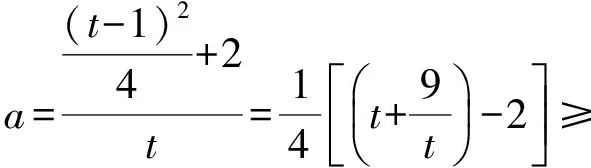

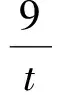
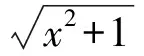
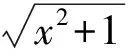
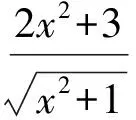
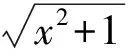
6 分离参数,用导数工具求取值范围