有轨电车电子机械制动系统夹紧力控制优化方法

摘 "要：针对有轨电车电子机械制动（EMB）系统，提出一种夹紧力控制优化方法。首先建立EMB系统的数学模型，依据其物理结构及刚度非线性特性，将控制器设计为夹紧力控制层与转速控制两级控制结构。针对夹紧力控制层，仅考虑间隙消除与夹紧力的跟踪控制，采用速度曲线规划与夹紧力非线性PI控制相结合，以在期望时间内实现制动间隙快速消除；针对控制层，将系统中存在不确定扰动等效于综合干扰项，提出一种自适应增益超螺旋算法（AGSTA），提高了电机控制层对未知干扰的鲁棒性及速度跟踪的快速性，减小转速超调，使EMB系统的夹紧力保持一致。仿真及实验结果表明，所提出的夹紧力控制优化方法能够有效地改善系统的控制性能。

关键词：有轨电车；电子机械制动系统；夹紧力控制；无刷直流电机；Super-Twisting算法

DOI：10.15938/j.emc.（编辑填写）

中图分类号：TM921.5 " " " " " " 文献标志码：A " " " " "文章编号：1007-449X（2024）07-0000-00（编辑填写）

Optimization control method for clamping force of electromechanical brake system of tram

ZHAO Yiyun， LIN Hui， LI Bingqiang

（School of Automation， Northwestern Polytechnical University， Xi’an 710129， China）

Abstract： An optimization control method for clamping force is proposed for the electromechanical brake （EMB） system of trams. Firstly， the model of the EMB system is established， and the controller is divided into a clamping force control layer and speed control layer according to its physical structure and stiffness nonlinear characteristics. Only the clearance elimination and clamping force tracking control are considered for the clamping force control layer. The speed curve planning is combined with clamping force nonlinear PI control to quickly eliminate the braking gap in the desired time. For the speed control layer， the nonlinear factors in the system are equivalent to the comprehensive interference. Meanwhile， an adaptive gain super-twisting algorithm （AGSTA） is proposed to improve the robustness of unknown interference and the rapidity of speed tracking of the motor control layer， which can reduce speed overshoot and keep the clamping force of the EMB system consistent. Finally， the simulation and experimental results show that the proposed optimization control method of clamping force can effectively improve the control performance of the system.

Keywords： tram; electromechanical brake system; clamping force control; brushless DC motor; Super-Twisting algorithm

0 引 "言

电子机械制动（electromechanical brake， EMB）系统具有智能化、轻量化、高安全性等优点，因而成为下一代列车制动技术的主要选择[1-3]。EMB系统采用机电一体化设计，将驱动电机、减速机、滚珠丝杠与传感器高度集成化，利用电能直接驱动摩擦副，从而产生制动转矩[4]。然而，EMB系统是一个多变量、强耦合的复杂系统，其中存在着刚度非线性、摩擦非线性及未建模动态等其它不确定干扰[5-7]。因此，如何实现夹紧力的高性能控制，已成为EMB系统研发的关键问题之一。

为实现EMB系统的夹紧力优化控制，相关学者在航空、汽车及轨道交通领域展开了大量研究。目前常用的方法主要包括：线性控制[8-9]、近似时间最优控制[10]、滑模控制[11]和模糊控制[12-13]等。基于经典运动控制架构，文献[8]采用了压力、速度和内部电流控制回路为级联结构的比例积分（proportional-integral， PI）控制器实现夹紧力的闭环控制。针对列车EMB系统，文献[9]提出了夹紧力的优化控制算法，将跟踪微分器与PI控制相结合，引入缓冲过程，确保系统的无超调运行。但上述两种方法忽略了系统中存在的参数摄动及未建模动态等未知干扰。文献[10]将鲁棒近时间最优控制应用于汽车EMB系统中，实验结果表明其控制性能优于级联式PI控制算法，但其依赖于系统的精确模型，计算较为复杂。针对飞机全电式刹车系统具有的高阶非线性特点，文献[11]中考虑刹车作动机构的非线性负载扰动，通过非线性干扰观测器与快速终端滑模控制相结合，从而实现对未知扰动的抑制，提高系统的伺服性能与控制精度，但算法使得系统速度不可控，从而造成刹车压力超调。文献[12-13]将模糊矫正器引入滑模控制对切换控制量进行修正，以增强系统的抗干扰能力，其有效性于EMB硬件在环实验中得到验证，但其依赖于较高的系统调试经验。文献[14]利用最大转矩电流比控制方法对EMB系统的永磁同步电机控制进行优化，降低了能耗，但忽略了对系统的动态性能与抗扰能力的提升。依据制动盘技术规范，低地板有轨电车的“七段式”制动方式使得期望夹紧力处于阶跃跳变状态。EMB系统具有强非线性的特点，难以建立其夹紧力与速度的精确模型。当EMB系统的输出夹紧力跟随期望值跳变时，电机转速也会产生较为明显的突变，使得系统夹紧力超调，出现制动不一致的情况，无法保证车辆安全运行。为保证EMB系统的动态性能及控制精度，对于系统的电机转速要求具有较为理想的跟踪性能。因此，本文对EMB系统的速度环动态性能进行优化，将系统中存在不确定干扰等效为综合扰动，解决超调量与动态性能的矛盾，以改善夹紧力的跟踪效果。

基于上述分析，本文针对某型号100%低地板有轨电车EMB系统，提出一种夹紧力控制优化方法。其创新性主要体现在：首先，阐述了EMB系统的结构及工作原理，建立其相应的数学模型。随后考虑EMB系统中存在的不确定干扰及刚度非线性特性，将控制器分为夹紧力控制层与电机控制层两个部分。对于夹紧力控制，采用速度曲线规划设计与非线性PI控制相结合，以保证夹紧力控制精度的同时快速消除制动间隙。其次，在电机控制层中，针对系统中存在的综合扰动及转速突变，提出一种自适应增益超螺旋算法（adaptive gain super-twisting algorithm， AGSTA），与常规方法相比较，提高了电机速度环对未知干扰的鲁棒性及速度跟踪的快速性，从而改善速度环的控制性能，适用于低地板有轨电车“七段式”制动EMB系统。最后，仿真及实验结果表明所提出的夹紧力控制优化方法能够有效地提高系统的控制性能，实现EMB系统的无超调高精度伺服控制。

1 电子机械制动系统数学模型

1.1 系统描述

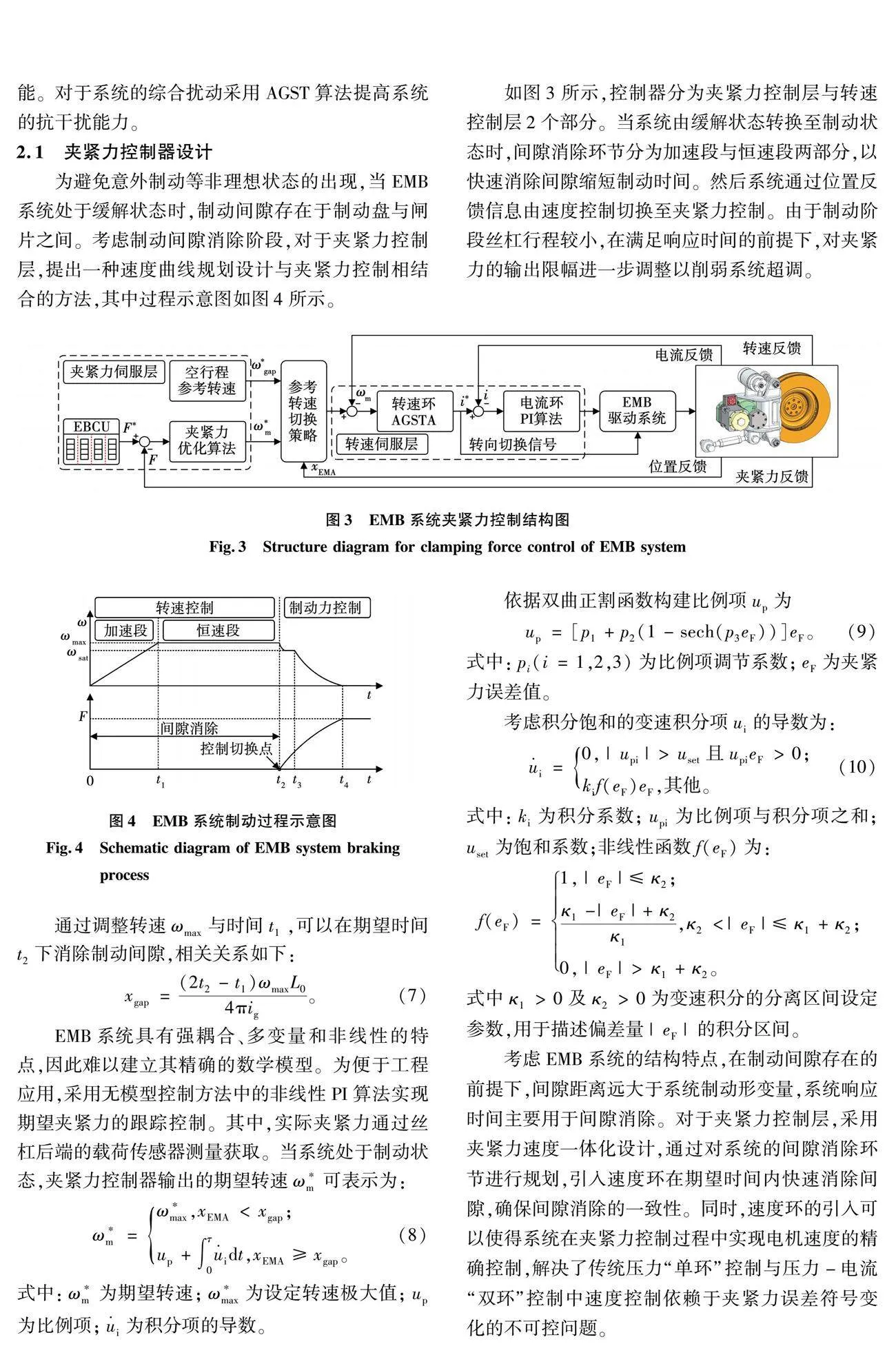
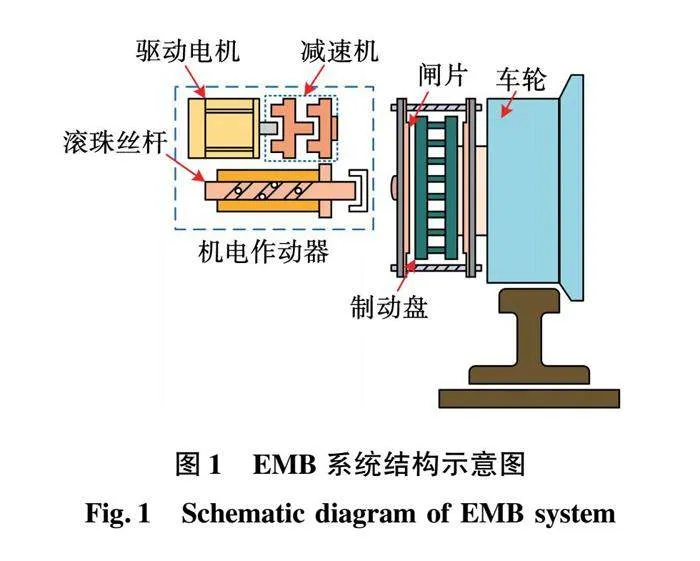
EMB系统的主要任务为接收电子制动控制单元（electronic braking control unit， EBCU）的制动指令，控制电机正反转运行，以实现目标夹紧力的精确跟踪，其结构示意图如图1所示。

机电作动器（electromechanical actuator， EMA）作为EMB系统的动力输出单元，其中滚珠丝杠副将经行星减速机传递的电机旋转运动变成轴向运动，进而推动杠杆，使得夹钳结构件上的闸片在推力的作用下与制动盘产生夹紧力，从而提供制动转矩，达到制动的效果。

1.2 系统数学模型

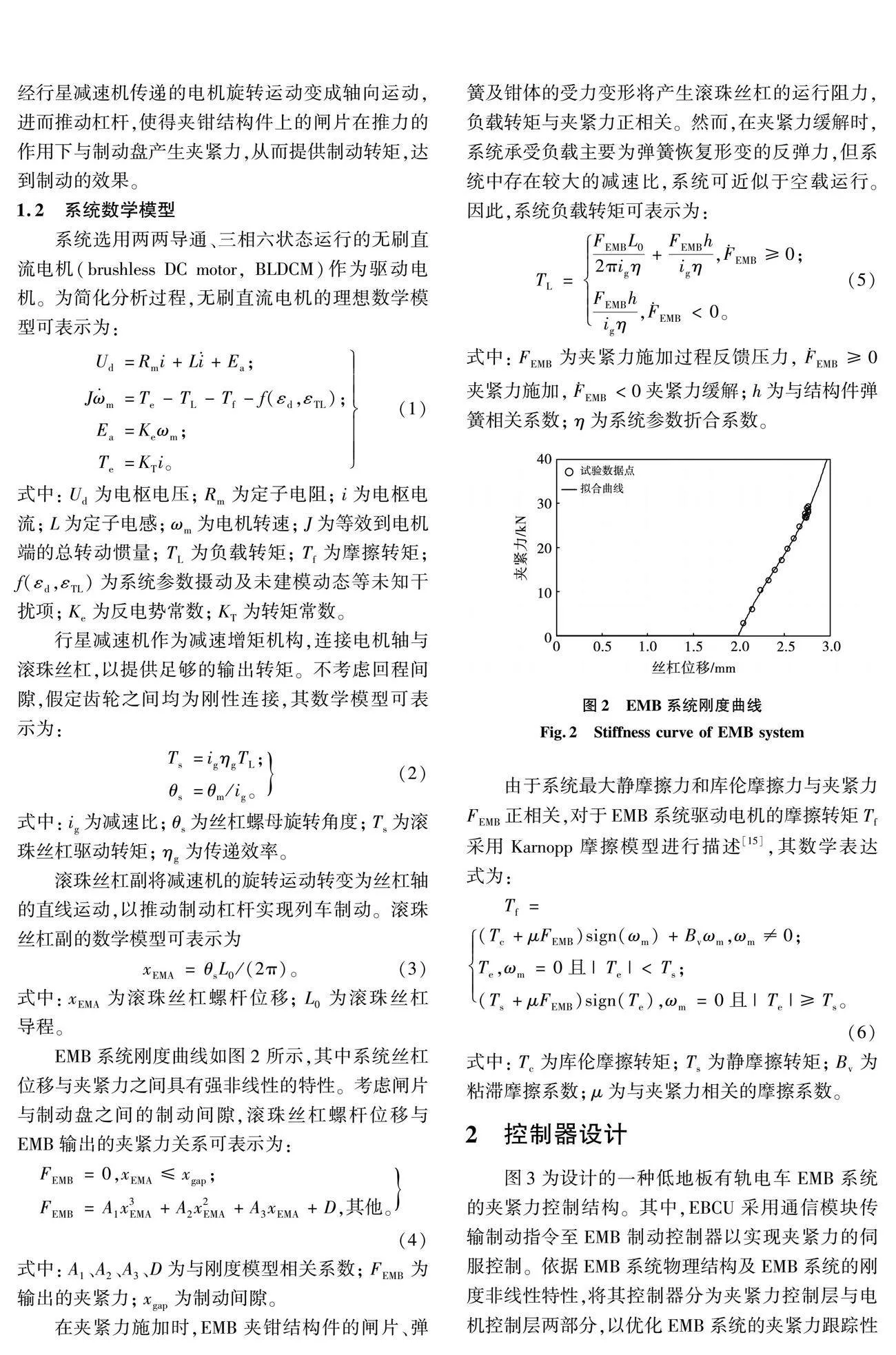
系统选用两两导通、三相六状态运行的无刷直流电机（brushless DC motor， BLDCM）作为驱动电机。为简化分析过程，无刷直流电机的理想数学模型可表示为：

2 系统仿真分析

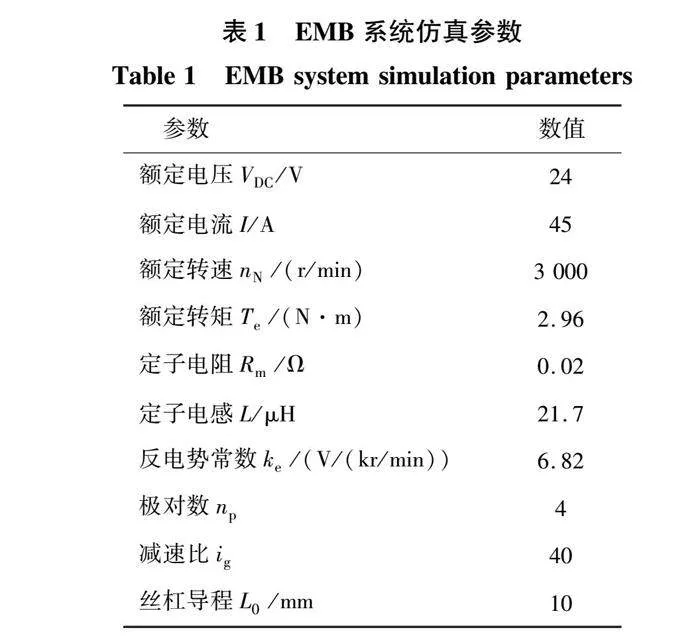
在MATLAB/Simulink环境下搭建EMB系统仿真模型，以验证所提控制方法的有效性及优越性，仿真步长固定为1 µs。电流环采用PI控制。系统仿真模型中的EMB系统参数如表1所示。

系统仿真主要控制参数如下：

1）夹紧力控制器： ， ， ， ， ， 。

2）STA控制器： ， 。

3）AGSTA控制器： ， ， ， 。

4）电流控制器： ， 。

3.1 速度-电流双环仿真分析

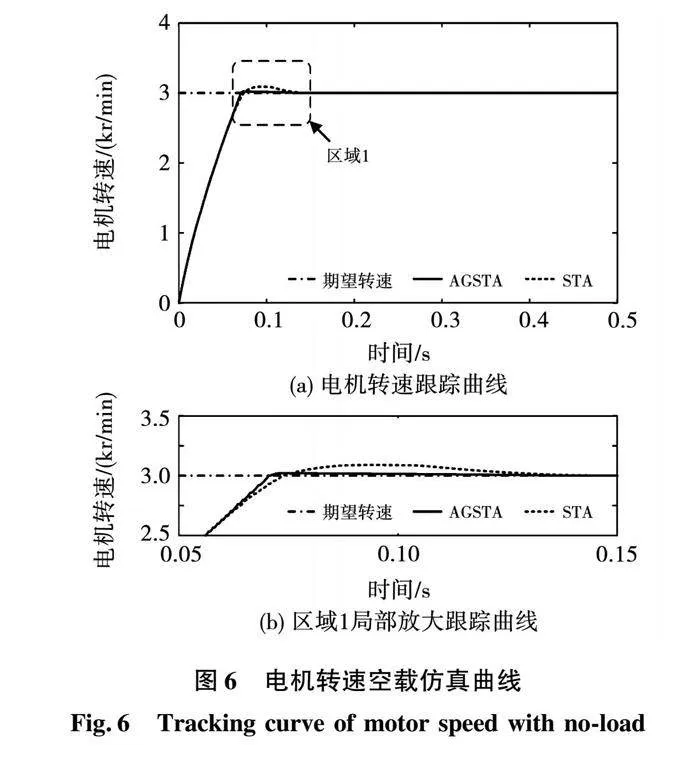
为验证AGSTA对常规方法的收敛速度与扰动抑制能力的改善，搭建速度-电流“双环”仿真模型，仿真结果如图6所示。

由局部放大图6（b）可知，空载情况下，给定电机转速阶跃转速指令信号 ，与常规STA相比较，采用AGSTA的转速超调量由3%降低为1%，且不影响系统的收敛时间。

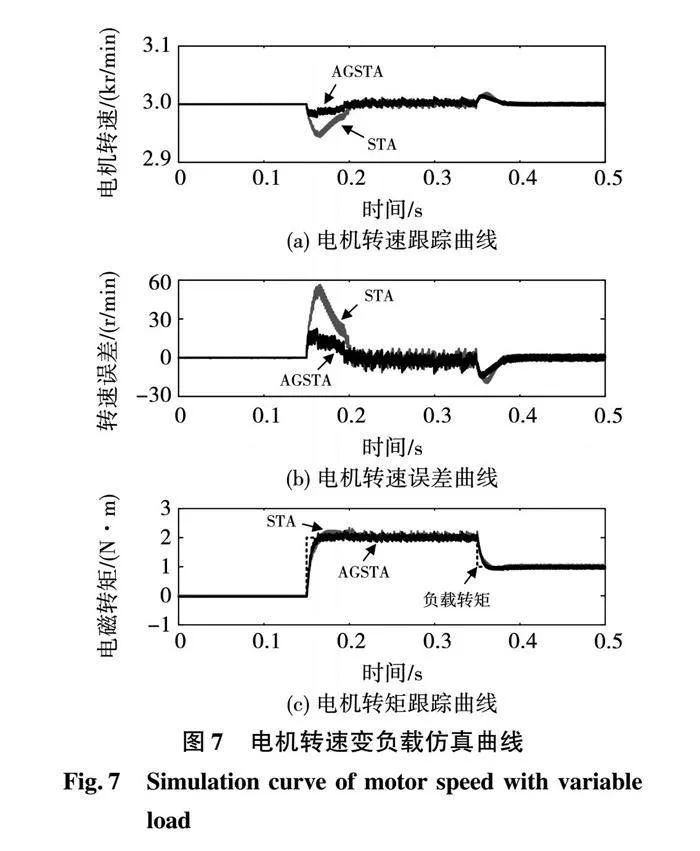
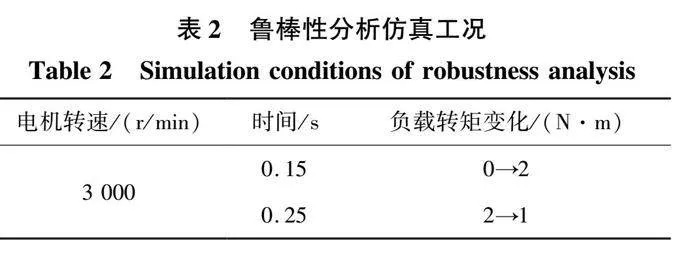
为了分析不同控制方法对负载扰动的鲁棒性，设置如表2所示的仿真工况。其中，期望转速恒定为3000 r/min，在不同的时间点对电机施加突变负载。图7为负载变化时采用不同控制方法的仿真对比曲线。

由图7（a）可知，在负载变化情况下，两种方法的速度跟踪曲线都出现了速度变化。图7（b）为变负载情况下的电机误差曲线，对比仿真结果可知，在0.15 s时电机负载突变导致采用STA的系统转速产生55 r/min的跌落，而采用AGSTA的系统转速波动为其4/11倍（20 r/min）。对比两种方法在0.25 s时的仿真结果，AGSTA使得系统转速波动为14 r/min，相较于STA减小6 r/min的波动。由图7（c）电机转矩跟踪曲线可知，对于负载转矩的变化，两种方法都能实现相应的转矩输出，而AGSTA的响应速度略优于传统STA方法。

由仿真结果可知，通过引入非线性函数构建的AGSTA可以优化电机转速的控制性能，并使得系统的负载扰动抑制能力得到改善。为EMB系统的夹紧力控制优化提供基础。

3.2 EMB系统仿真分析

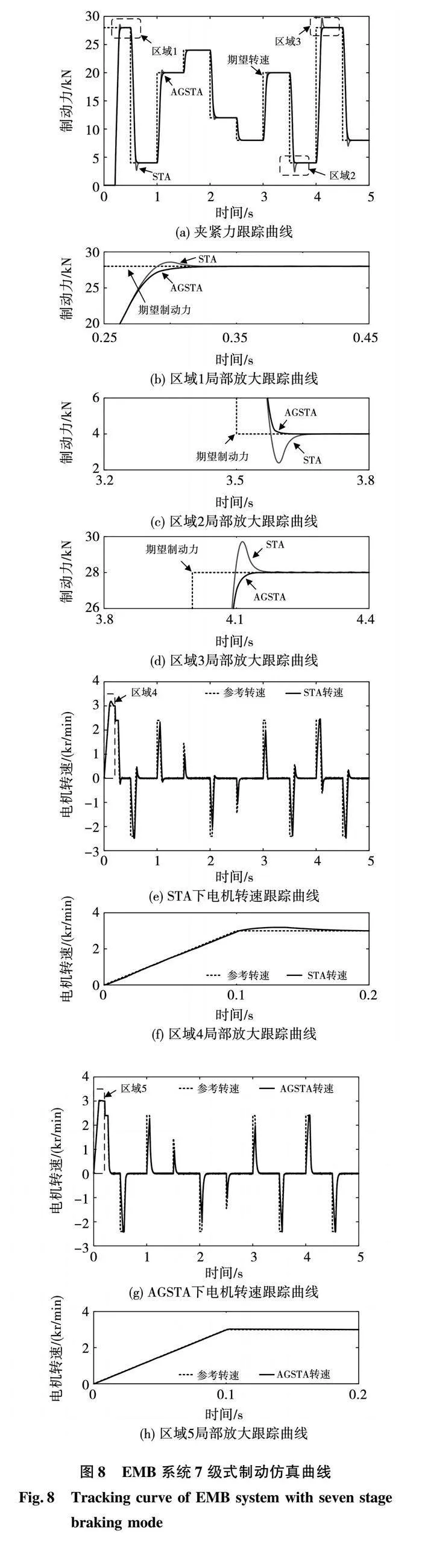
为进一步验证算法优化对EMB系统夹紧力控制性能的提升，结合低地板有轨电车7级制动模式，以4 kN为间隔值设定随机制动挡位切换仿真实验， 仿真工况具体如下：目标制动挡位依次为28 kN→4 kN→20 kN→24 kN→12 kN→8 kN→20 kN→4 kN→28 kN，每个档位保持时间为0.5 s。

图8为EMB系统7级式制动仿真曲线，由图8（a）、（f）及（h）可知，电机在制动初始阶段采用速度-电流“双环”控制策略以快速消除制动间隙。

对比STA与AGSTA两种方法，AGSTA具备更加出色的速度跟踪性能，亦使得EMB系统无超调现象发生。与之相反，从图8（b）可知采用STA算法由于动态性能的劣势导致夹紧力控制出现了2.2%的超调。此外，对比两种方法下的夹紧力跟踪对比曲线，区域2及区域3中夹紧力变化较大时，皆出现了较大的超调现象。特别地，区域3中超调现象最为明显。作为区域2的局部放大跟踪曲线，图8（b）表明仿真结果出的最大的超调为1.6 kN。此外，对比其中的速度仿真曲线ASTA算法使得系统的电机转速跟踪效果提升，改善控制性能，使得系统能够实现速度曲线规划以实现制动间隙的可控消除。同时，结合夹紧力非线性PI控制实现了夹紧力的无超调控制。

3 实验结果与分析

4.1 EMB实验平台搭建

为验证上述控制策略的有效性，搭建如图9所示的EMB性能测试平台进行实验验证。本实验平台主要由夹钳结构件、制动盘、EMA样机、制动控制器、数据存储示波器及电源等组成。选用Panasonic MSME152GCGM型号的伺服电机及其驱动器以实现电机的动态加载实验。主控芯片选用Texas Instruments公司的TMS320F28335，逆变电路由N沟道场效应管CSD19506KCS构成，开关频率为20 kHz，驱动芯片选用UCC27211，电流测量采用ACS758，电机轴末端采用中空编码器测量电机转速，数据存储采用固纬数字存储示波器GDS-2104A，直流母线电压设定为24 V，电流环控制周期为0.1 ms，转速环控制周期为1 ms，夹紧力外环控制周期为5 ms。

4.2 实验结果与分析

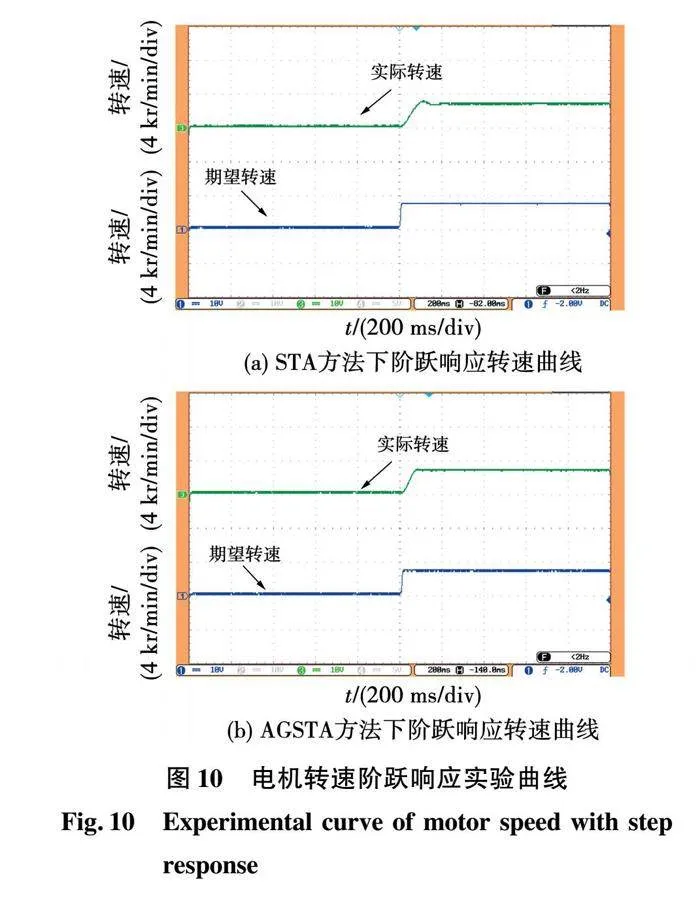
1）速度-电流双环实验分析。

图10为空载情况下，电机期望转速由初始300 r/min跳变至3 000 r/min时的实验曲线，可以看出，2种方法均能很好地跟随期望值。对比2种方法，STA方法中电机转速出现160 r/min的超调，与之相反AGSTA方法在不影响响应时间的前提下，加快收敛速度，实现了电机转速的无超调控制。

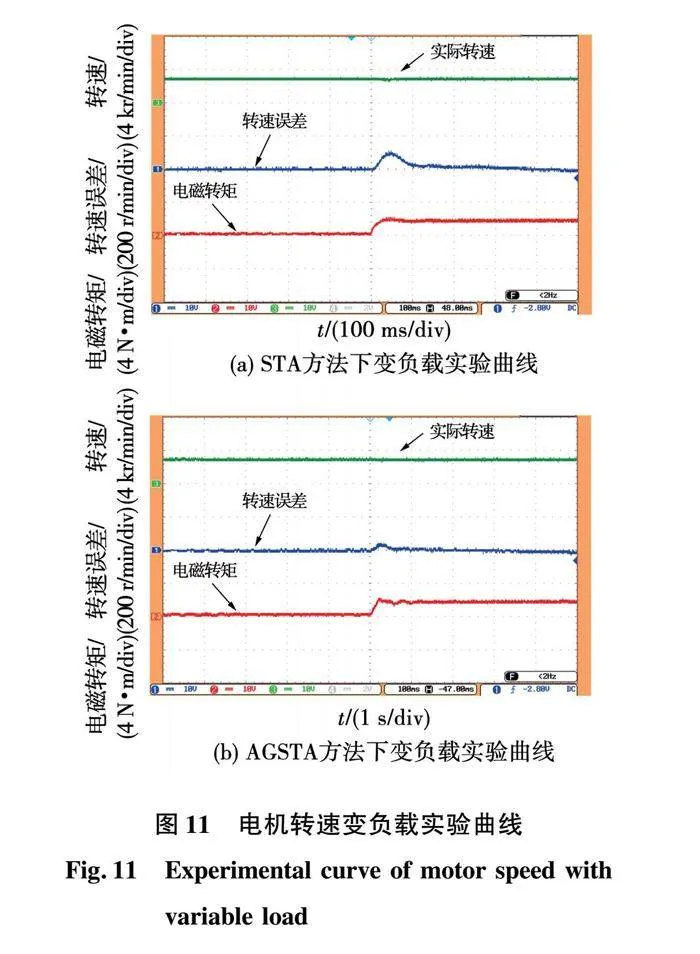
图11为期望转速3 000 r/min下，对电机突加2 Nm负载的实验曲线。由图11可知，2种方法在突加负载后均可迅速达到稳态。

然而，常规STA方法使得电机出现95 r/min的转速跌落。与之相反，AGSTA方法下的转速跌落量为其8/19倍40 r/min。因而在突加阶跃负载时，AGSTA方法下的转速波动更小，验证了所提出的改进型Super-Twisting控制器具有较强的抗负载扰动能力。

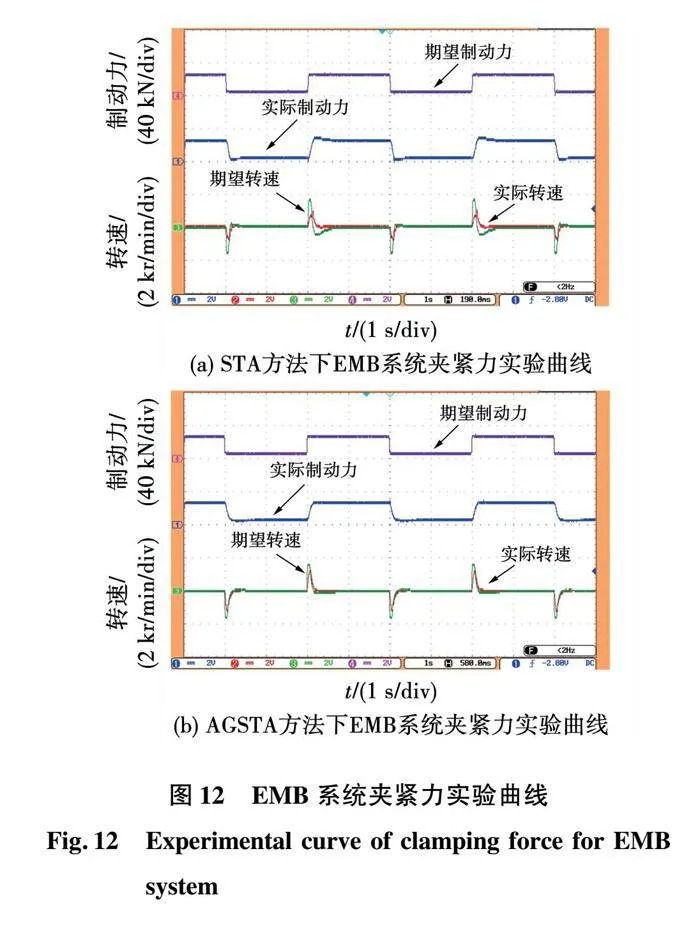
2）EMB系统实验分析。

结合实际EMB系统，进行夹紧力跟踪实验，设定期望夹紧力值为方波信号，其峰峰值为8～28 kN，频率为0.25 Hz，实验结果如图12所示。其中，实验从上至下为期望夹紧力、实际夹紧力、期望转速及实际转速。由图12（a）可知，STA方法下的EMB系统在上跳变和下跳中均出现了超调现象，易造成夹紧力不一致的情况。与之相反，由图12（b）可知，采用AGSTA算法对EMB控制系统的速度环进行优化能够处理制动模式下系统动态性能与超调之间的矛盾问题，从而提高EMB系统的夹紧力跟踪性能与有轨电车运行的安全性。

4 结 论

针对具有不确定扰动及刚度非线性特性的低地板有轨电车EMB系统，本文提出一种夹紧力控制优化方法，其中控制器由夹紧力控制层与转速控制层两级控制结构组成，具有如下优势：

1）对于夹紧力控制层，采用速度曲线规划与夹紧力非线性PI控制相结合，以快速消除制动间隙，确保夹紧力的控制精度。

2）对于转速控制层，将系统中存在的参数不确定性及未知扰动等效于综合干扰项，提出一种自适应增益超螺旋算法，以提高系统的鲁棒性及速度跟踪的快速性，改善夹紧力的控制性能。

仿真及实验结果表明，相较于常规STA，本文所提出的AGSTA在不影响响应时间的前提下，使得速度-电流“双环”中的转速超调量得到改善。同时，将优化算法应用于EMB系统中，实现了夹紧力的无超调高精度伺服控制。

参 考 文 献：

[1] 吴萌岭， 马天和， 田春， 等. 列车制动技术发展趋势探讨[J].中国铁道科学， 2019， 40（1）： 134.

WU Mengling， MA Tianhe， TIAN Chun， et al. Discussion on development trend of train braking technology[J]. China Railway Science， 2019， 40（1）： 134.

[2] OH H K， BEAK S K， JEON C S. Structural analysis of power transmission mechanism of electro-mechanical brake device for high speed train[J]. Journal of the Korea Academia-Industrial， 2019， 20（12）： 535.

[3] 王健. 城市轨道交通电机械制动系统总体设计方案和关键技术研究[J].现代城市轨道交通， 2020， （11）： 36.

WANG Jian. Research on overall design scheme and key technology of electromechanical braking system for urban rail transit[J]. Modern Urban Transit， 2020， （11）： 36.

[4] 杨磊， 苗峰， 王帅， 等. 电子机械制动夹钳的设计及其试验研究[J].机电工程， 2022， 39（5）： 648.

YANG Lei， MIAO Feng， WANG Shuai， et al. Design and experimental research of electronic mechanical brake clamp[J]. Journal of Mechanical ＆ Electrical Engineering， 2022， 39（5）： 648.

[5] RAO Y， LI YR， LIANG B， et al. LADRC-based disturbance rejection method for EMA in aircraft braking system[C]// 24th International Conference on Electrical Machines and Systems （ICEMS）， October 31-November 3， 2021， Gyeongju， Korea. 2021： 909-914.

[6] LI Y J， SHIM T， SHIN D H， et al. Control system design for electromechanical brake system using novel clamping force model and estimator [J]. IEEE Transactions on Vehicular Technology， 2021， 70（9）： 8653.

[7] 相里康. 飞机全电刹车力伺服控制与可靠驱动技术研究[D]. 西安：西北工业大学， 2018.

[8] XU Z， GERADA C. Enhanced force estimation for electromechanical brake actuators in transportation vehicles[J]. IEEE Transactions on Power Electronics， 2021， 36（12）： 14329.

[9] 吴萌岭， 雷驰， 陈茂林. 基于列车电机械制动系统夹紧力的控制算法优化[J].同济大学学报（自然科学版）， 2020， 48（6）： 898.

WU Mengling， LEI Chi， CHEN Maolin. Control algorithm optimization of clamping force based on train electro-mechanical braking system[J]. Journal of Tongji University （Natural Science）， 2020， 48（6）： 898.

[10] LEE C F， MANZIE C. Near-time-optimal tracking controller design for an automotive electromechanical brake[J]. Proceedings of the Institution of Mechanical Engineers， Part I： Journal of Systems and Control Engineering， 2012， 226（4）： 537.

[11] MA R， ZHANG H Y， YUAN M H， et al. Chattering suppression fast terminal sliding mode control for aircraft EMA braking system[J]. IEEE Transactions on Transportation Electrification， 2021， 7（3）： 1901.

[12] 彭晓燕， 何磊， 吕以滨. 基于滑移率的电子机械制动模糊滑模控制[J]. 中南大学学报（自然科学版）， 2018， 49（2）： 360.

PENG Xiaoyan， HE Lei， LU Yibin. Fuzzy sliding mode control based on vehicle slip ratio for electro-mechanical braking systems[J]. Journal of Central South University （Science and Technology）， 2018， 49（2）： 360.

[13] PENG X Y， JIA M F， HE L， et al. Fuzzy sliding mode control based on longitudinal force estimation for electro-mechanical braking systems using BLDC motor[J]. CES Transactions on Electrical Machines and Systems， 2018， 2（1）： 142.

[14] BEAK S K， OH H K， PARK J H， et al. Evaluation of efficient operation for electromechanical brake using maximum torque per ampere control[J]. Energies， 2019， 12（10）： 1869.

[15] CHEN P C， WU J， ZHAO J， et al. Design and position control of a novel electric brake booster[J]. SAE International Journal of Passenger Cars-Mechanical Systems， 2018， 11： 389.

[16] 刘文吉，杜佳璐，李健，等. 基于超螺旋滑模的船载稳定平台镇定控制[J]. 系统工程与电子技术， 2022， 44（5）： 1662.

LIU Wenji， DU Jialu， LI Jian， et al. Stabilization control for vessel-borne stabilization platform based on super-twisting sliding mode[J]. Systems Engineering and Electronics， 2022， 44（5）： 1662.

[17] 罗世彬，李晓栋，王忠森，等. 并联式运载器上升段广义超螺旋有限时间控制[J]. 系统工程与电子技术， 2022， 44（5）： 1626.

LUO Shibin， LI Xiaodong， WANG Zhongsen， et al. Generalized super-twisting finite-time control for the ascent phase of parallel carrier [J]. Systems Engineering and Electronics， 2022， 44（5）： 1626.

[18] 李鹏，郑志强. 基于类二次型Lyapunov函数的Super-twisting算法收敛性分析[J]. 控制与决策， 2011， 26（6）： 949.

LI Peng， ZHENG Zhiqiang. Convergence of Super-twisting algorithm based on quadratic-like Lyapunov function[J]. Control and Decision， 2011， 26（6）： 949.