模糊PID变结构自适应算法在无人车转向电机矢量控制中的应用

摘 "要：针对无人车线控转向系统电机矢量控制问题，提出一种模糊PID变结构自适应控制算法。依据电机模型推导出滑模变结构控制的趋近律和控制律，为避免控制器设计过程中对系统参数的依赖，采用PID控制器替换滑模变结构控制中的等效控制量。使用模糊方法分别对PID控制器的参数和趋近律参数进行动态调整，使其具备自适应能力以及降低或消除系统状态接近滑模面时的“抖振”现象。利用李雅普诺夫理论证明了该方法的全局稳定性。仿真实验结果表明无论系统在阶跃响应还是正弦响应工况下，模糊PID变结构自适应控制方法在系统响应速度和对负载波动的抑制方面都明显优于模糊PID方法和传统的滑模变结构方法。

关键词：无人车；线控转向；永磁同步电机；模糊推理；滑模控制；矢量控制

DOI：

中图分类号：TM351；TP273 " " " " " "文献标志码：A " " " " "文章编号：

Application of fuzzy PID variable structure adaptive algorithm in

steering motor vector control of unmanned vehicles

LI Jianshi， PAN Shiju， LOU Jingtao， LI Yongle， XU Youchun

（Institute of Military Transportation， Army Military Transportation University， Tianjin 300161， China）

Abstract： Aiming at the motor vector control problem of the steer-by-wire steering system of unmanned vehicle， a fuzzy PID variable structure adaptive algorithm is proposed. According to the motor model， the proximity law and control law of sliding mode variable structure control are derived， and in order to avoid the dependence on system parameters in the process of controller design， a PID controller is used to replace the equivalent control variables in sliding mode variable structure control. The parameters of the PID controller and the proximity law parameters are dynamically adjusted using the fuzzy method to make it adaptive to reduce or eliminate the \"jitter\" phenomenon when the system state is close to the sliding mode surface. The global stability of the method was proved by using Lyapunov's theory. Simulation experiments show that the fuzzy PID variable structure adaptive control method is significantly better than the fuzzy PID method and the traditional sliding mode variable structure method in terms of system response speed and suppression of load fluctuations， regardless of whether the system is in step response or sinusoidal response.

Keywords： unmanned vehicle; steer-by-wire; permanent magnet synchronous motor; fuzzy reasoning; sliding mode control; vector control

0 引 "言

线控转向（steering-by-wire， SBW）技术是实现车辆自动驾驶的关键技术之一，无人车线控转向系统使用转向电机提供驱动力，根据车辆运动学和动力学原理，把车辆前轮目标转角转换成转向电机的参考转向角度，通过转向电机的位置伺服控制实现车辆前轮的快速精准的角度控制。因此，转向电机的控制性能直接影响车辆整体的转向控制效果。车辆转向系统机械连杆结构之间存在间隙，不平整道路或者不同路面会引起转向系统负载发生变化，这些原因决定了车辆转向系统具有较强的非线性和不确定性控制的特点，对转向系统控制器的设计提出了非常高的要求。线控转向系统转向电机多采用永磁同步电机（permanent magnet synchronous motor， PMSM）为动力元件[1]，于是永磁同步电机的位置伺服控制就成了无人车线控转向系统控制研究的重点和难点。

由于车辆线控转向控制系统具有强非线性特性，传统的PID控制作为典型的线性控制方法，通常无法取得理想的控制效果。滑模变结构控制是一种鲁棒性很强的非线性控制方法，在一定条件下对外界干扰和参数扰动具有不变性，其关键点是保证滑模运动的存在和系统进入滑模面以后具有良好的运动特性[2]。在实际的控制过程中，为了使系统保持在滑模面上运动，需要在不同的控制逻辑间不停的切换，容易引起系统的抖动[3]。同时滑模变结构控制的设计依赖精确的系统模型和参数，在无法获得系统精确模型和参数的情况下，传统的滑模变结构控制方法就很难达到理想的控制效果。随着人工智能技术的发展，一些控制方法如模糊控制、神经网络控制等具有很好的自学习和自适应能力。单纯的智能控制，如自适应控制对外负载的变化过于敏感而且依赖设计人员的设计经验[4]；模糊控制很多模糊规则之间会相互制约[5]；神经网络方法在控制过程中需要对模型参数实时计算，需要较强的硬件支持[6]，因此单纯的智能控制方法也很难达到理想的控制效果。有学者将智能控制方法与传统的控制方法相结合，以此追求更好的控制效果，例如将模糊神经网络与滑模控制相结合，用于永磁直线同步电机的位置控制中，在系统参数变化和外部扰动存在的情况下获得了很好的控制效果[7]。

本文针对线控转向电机矢量控制的响应速度和抗负载波动能力等难点问题，提出一种模糊PID变结构自适应控制算法。以线控转向系统的核心部件——永磁同步电机为研究对象，基于电机的状态空间模型求出滑模变结构控制的趋近律和控制律。为避免控制器设计过程中对系统参数的依赖，采用PID控制替换滑模变结构控制中的等效控制量。利用模糊方法分别对PID的参数和趋近律参数进行动态调整，使其具备自适应能力以降低或消除系统接近滑模面时的“抖振”现象。利用李雅普诺夫理论证明了该方法的全局稳定性。基于MATLAB-Simulink构建了永磁同步电机模型，仿真实验表明系统在阶跃响应和正弦响应工况下，模糊PID变结构自适应控制方法在系统响应速度和对负载波动的抑制方面都明显优于模糊PID方法和传统的滑模变结构方法。

1 永磁同步电机数学模型

永磁同步电机在d-q轴坐标系下的数学模型可以表示[8]为：

因此，在满足式（13）的情况下， 是负定矩阵。由李雅普诺夫第二方法判定系统在模糊PID变结构自适应控制器的作用下是全局稳定的[11]。

2 仿真实验

在MATLAB中构建永磁同步电机位置伺服系统的仿真模型来对所提出的模糊PID变结构自适应控制方法进行验证。

仿真所采用的电机主要参数如表2所示。

模糊PID变结构自适应控制器的主要设计参数包括：滑模面函数的系数 =200；变结构模糊推理中的输入论域分别为跟踪误差限定为 ；而滑模面函数值限定为 ； 的初始值为7.0， 的初始值为6.0， 的初始值为0.1。

为了验证所提出的模糊PID变结构自适应控制方法的性能，分别与传统滑模变结构方法和模糊PID方法这两种控制方法进行对比。其中模糊PID方法所用参数与所提出的模糊PID变结构自适应控制方法中模糊部分的相关参数一致。传统滑模变结构控制则按照前述已知电机的参数来进行设计，需要说明的是在设计过程中由于无法预知负载变化情况，因此等效控制量求取过程中假设负载相关项 =0。

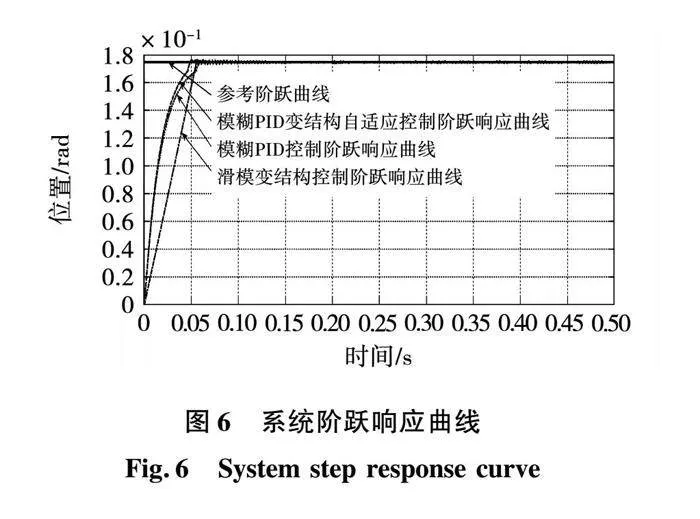
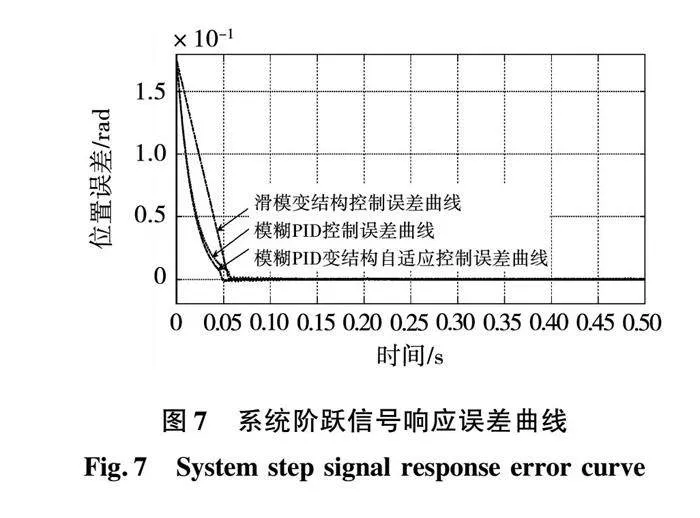
在负载扰动情况下考察不同控制方法的跟踪精度和鲁棒性表现。图6为系统阶跃响应曲线，图7为系统阶跃响应误差曲线。总体而言，3种控制方法都表现出了良好的跟踪效果，但是通过对误差曲线的对比可以发现，滑模变结构控制方法在达到稳态之后出现了明显的抖振现象，与之对应的另外两种控制方法则表现相对稳定。另外，从系统响应时间来看，本文所提出的模糊PID变结构自适应控制器的响应速度最快，充分体现出了趋近律自适应性所带来的优点。另外图中一个值得注意的现象是传统滑模变结构控制的上升过程近似为直线，而固定的趋近律系数正是造成这一结果的主要原因。

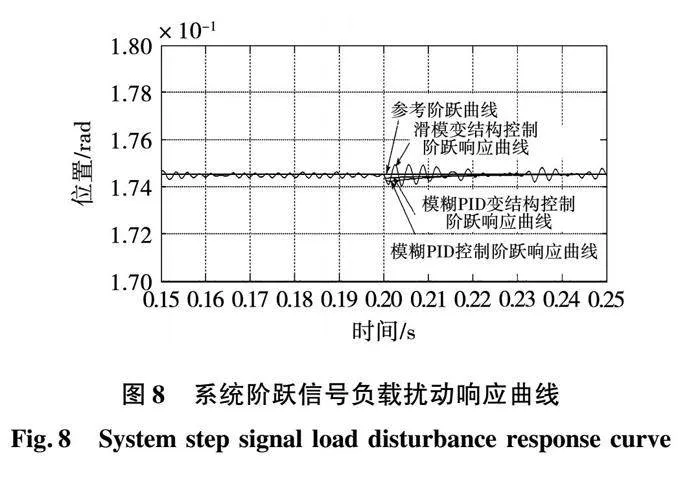
当系统进入稳定状态后，在0.2 s时给系统施加20 N·m的负载，3种方法的表现如图8所示。图中传统滑模变结构控制方法因为抖振的原因，虽然跟踪效果相对较差，但从波动趋势变化上可以分析出负载对其影响并不明显。模糊PID控制则对负载的变化十分敏感，误差产生了明显的突变，并需要较长时间才能恢复到稳定状态。而模糊PID变结构自适应控制方法无论是在稳定性还是对负载波动的抑制上都明显优于其它2种方法，表现出了良好的鲁棒特性。

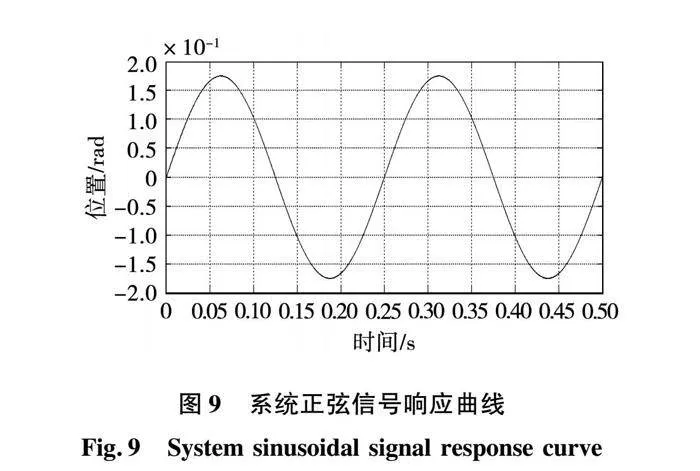
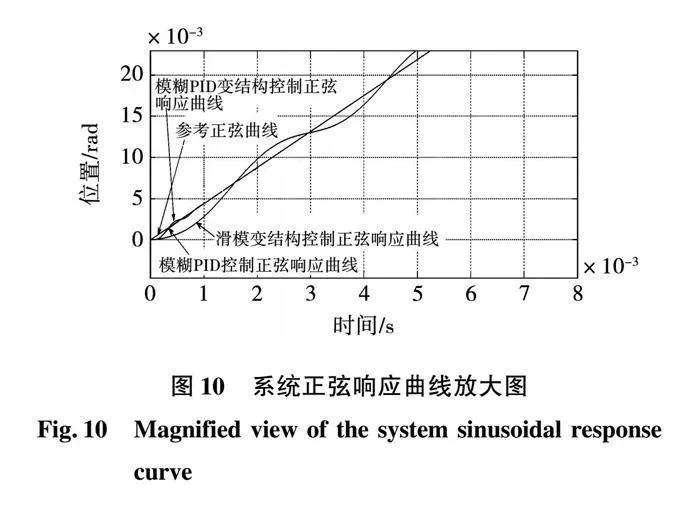
为了进一步评估负载扰动情况下的动态表现，仿真设计了频率4 Hz、幅度 的正弦运动的跟踪实验。图9显示各种控制方法都表现出了良好的跟踪效果。

为了能够更直观的看出3种控制器的细节差别，给出了图10所示的局部放大图。从图10可以看出模糊PID变结构自适应控制和模糊PID控制均得到了很好的跟踪效果，滑模变结构控制则出现了穿越现象，这实质上是抖振问题的间接体现。

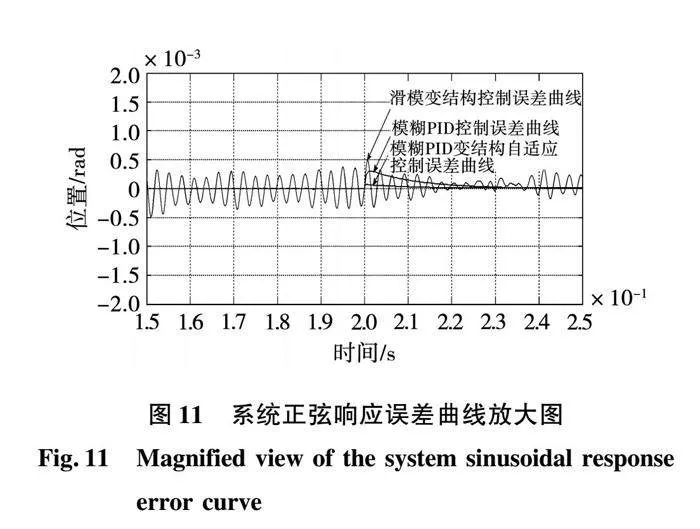
从图11所给出的误差曲线比对中可以看出滑模变结构控制存在抖振现象。同时，还可以看出的是，当0.2 s时给系统施加20 N·m的外负载后，模糊PID变结构自适应控制方法对外负载变化的响应最不敏感，且能最快地恢复到原有状态，与静态试验一样表现出了很好的鲁棒性。

针对系统参数不确定性问题进行仿真分析，转向电机在工作过程中除了面临电压波动这一不确定性因素外，另一个潜在的不确定性因素是由发热而导致的电枢电阻温漂，从而造成电阻的增加。因此仿真实验设计中，在电枢电压中叠加了一个功率谱为[0， 0.01]的有限带宽白噪声，实现电压的波动范围在（-10 V， 10 V）之间；同时，将电枢电压从定值改变为一个初值为0.19Ω，0.2 s阶跃至1.00Ω的可变值。

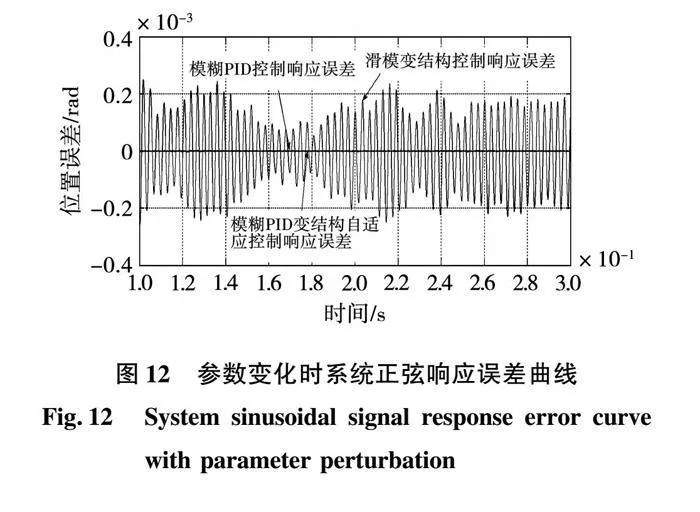
在上述参数不确定性条件下进行3种控制方法的空载正弦跟踪仿真。结果显示不同控制方法的总体跟踪效果均表现良好，图12给出了误差的局部对比放大曲线。

从图12中可以看出，转向电机系统的参数不确定性并没有对3种控制方法的跟踪效果和鲁棒性造成显著的影响，尤其是0.2 s处的电阻值阶跃变化没有在误差曲线上明显地反映出来。一方面，供电电压波动范围和发热引起的电阻值变化量都相对较小，并没有从本质上改变永磁同步电机的运动特性，因此参数不确定性对系统的影响不如负载扰动造成的影响明显。另一方面，3种非线性控制方法都具备的鲁棒特性也能够抑制参数不确定性的影响效果，因此整个系统最终表现出了图12所示相对稳定的跟踪误差。但是，从图12可以看出滑模变结构控制结果相比于模糊PID变结构自适应控制结果出现了一定程度的“抖振”现象，这也证明了本文提出的模糊PID变结构自适应控制算法由于模糊规则的加入，能够削弱甚至消除滑模变结构控制中的“抖振”现象。

通过上述仿真结果分析，可以得出本文提出的模糊PID变结构自适应控制方法相比于滑模变结构控制有效改善了抖振问题，总体上在控制精度、收敛速度和抗负载干扰能力等方面表现更好。

3 结 "论

本文将PID控制和滑模变结构控制相结合，提出了模糊PID变结构自适应控制算法，其中PID作为控制器的线性控制项，变结构作为控制器的非线性控制项。该方法能够在系统模型参数不确定的情况下对无人车线控转向系统的永磁同步电机进行快速和精准的位置伺服控制。仿真结果表明该由于模糊规则的加入，在一定程度上能够消除滑模变结构控制的抖振现象，具有很好的鲁棒性，而且系统在阶跃信号和正弦信号控制工况下，模糊PID变结构自适应控制方法在系统响应速度和对负载波动的抑制方面都明显优于模糊PID方法和传统的滑模变结构方法。

本文所提出的模糊PID变结构自适应控制算法具有结构简单、精度高、鲁棒性良好的优点，适用于线控底盘转向电机的控制，为无人驾驶汽车精准的转向控制奠定基础。

参 考 文 献：

[1] 张虎. 基于永磁同步电机的电动助力转向系统力矩控制算法研究[D]. 长春： 吉林大学， 2015.

[2] 崔家瑞， 高江峰， 张波， 等. 永磁同步电机滑模变结构鲁棒控制[J]. 电机与控制学报， 2016， 20（5） ： 84.

CUI Jiarui， GAO Jiangfeng， ZHANG Bo， et al. Robust control of synchronous motor based on sliding mode variable structure[J]. Electric Machines and Control， 2016， 20（5） ：84.

[3] 潘雄杰， 赵世伟， 杨向宇， 等. 基于渐近趋近律的永磁同步电机滑模控制研究[J]. 微特电机， 2022， 50（5） ：57.

PAN Xiongjie， ZHAO Shiwei， YUANG Xiangyu， et al. nbsp;Research on sliding mode control of PMSM based on asymptotic reaching law[J]. Small and Special Electrical Machines， 2022， 50（5） ：57.

[4] 方靖荃， 邓文翔， 姚建勇， 等. 电机伺服系统快速自适应抗扰控制[J]. 西安交通大学学报， 2021， 55（6）：44.

FANG Jingquan， DENG Wenxiang， YAO Jianyong， et al. A fast adaptive disturbance rejection control for motor servo systems[J]. Journal of Xi’an Jiaotong University， 2021， 55（6） ：44.

[5] 宋丽君， 王燕. 一种无刷直流电机模糊自适应控制方法[J]. 制造技术与机床，2022（4） ：145.

SONG Lijun， WANG Yan. A fuzzy adaptive control method for brushless DC motor[J]. Manufacturing Technology amp; Machine Tool， 2022 （4） ：145.

[6] 丁豪， 于海生， 孟祥祥， 等. 永磁同步电机的神经网络滑模与预测控制[J/OL]. 控制工程（2022-08-01）[2022-09-16].https：//doi.org/10.14107/j.cnki.kzgc.20220242.

DING Hao， YU Haisheng， MENG Xiangxiang， et al. Neual network sliding mode and predictive control of permanent magnet synchronous motor[J/OL]. Control Engineering of China （2022-08-01）[2022-09-16]. https：//doi.org/10.14107/j.cnki.kzgc.20220242.

[7] 魏惠芳，王丽梅. 永磁直线同步电机自适应模糊神经网络时变滑模控制[J]. 电工技术学报， 2022， 37（4） ：861.

WEI Huifang， WANG Limei. Adaptive fuzzy neural network time-varying sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society， 2022， 37（4） ：861.

[8] 蔡沛. 永磁同步电机矢量控制及其关键参数整定方法研究[D]. 武汉： 华中科技大学， 2021.

[9] 胡涛， 申立群， 曹杰铭， 等. 电动伺服机构扰动补偿与神经网络模糊控制[J]. 电机与控制学报， 2023， 27（11）： 10.

HU Tao， SHEN Liqun， CAO Jieming， et al. Disturbance compensation and neural network fuzzy control of electric servo mechanism[J]. Electric Machines and Control， 2023， 27（11） ：10.

[10] 郭文韬， 单树清， 刘二林， 等. 无刷直流电机模糊PID控制及建模仿真[J]. 机电工程技术， 2021， 50（9） ：14.

GUO Wentao， SHAN Shuqing， LIU Erlin， et al. Fuzzy PID control and modeling simulation of brushless DC motor[J]. Mechanical amp; Electrical Engineering Technology， 2021， 50（9） ：14.

[11] 张懿， 陆腾飞， 魏海峰， 等. 电助力自行车模型参考自适应扭矩控制研究[J]. 电机与控制学报， 2022， 26（5） ：115.

ZHANG Yi， LU Tengfei， WEI Haifeng， et al. Model reference adaptive torque control of power-assist electric bicycle[J]. Electric Machines and Control， 2022， 26（5） ：115.