改进无模型自适应迭代学习的直线电机滑模控制

摘 "要：二维直线电机具有非线性、多变量及强耦合等特点，其精确模型无法获得，同时，在实际过程中由于参数摄动及扰动而造成的运行不稳定现象，致使对其跟踪控制十分困难。针对以上问题，根据无模型自适应迭代学习控制不依赖于被控系统精确数学模型的特点及滑模控制具有可设计且与对象参数和扰动无关的滑动模态，提出一种改进无模型自适应迭代学习的滑模结构复合控制策略。在无模型自适应迭代学习控制方案的准则函数中加入误差变化率，并对其收敛性进行分析论证；然后在紧格式动态线性化基础上，设计指数趋近律滑模控制，使改进无模型自适应迭代学习的滑模控制复合策略能够克服不稳定现象并具有很强的鲁棒性，从而进一步提高系统响应速度和控制精度。最后，通过仿真和实物验证，控制精度稳定在1μm范围内，并与其他控制方案相比，验证了所提方法的准确性和有效性。

关键词：改进无模型自适应迭代学习控制；误差变化率；准则函数；滑模控制；二维直线电机

DOI：10.15938/j.emc.（编辑填写）

中图分类号：TM359 " " " " " " 文献标志码：A " " " " "文章编号：1007 -449X（2017）00-0000-00（编辑填写）

Improved model free adaptive iterative learning control for

linear motor sliding mode control

ZHENG Xinxin， ZHANG Dahai， CAO Rongmin， HOU Zhongsheng

（1.School of Electrical and Engineering， Beijing Jiaotong University， Beijing 100044， China;

2.School of Automation， Beijing Information Science and Technology University， Beijing 100192， China

3.School of Automation， Qingdao University， Qingdao 266071，China）

Abstract： The two-dimensional linear motor is characterized by nonlinearity， uncertainty， multivariable and strong coupling， and its exact model is not available， meanwhile， the operational instability caused by parameter uptake and perturbation in the actual process makes its tracking control very difficult. To address the above problems， based on the characteristics of model free adaptive iterative learning control that does not depend on the accurate mathematical model of the controlled system and the sliding mode control that can be designed independently of the object parameters and perturbations， a composite control strategy is proposed to improve the model free adaptive iterative learning sliding mode structure. Then， the exponential convergence law sliding mode control is designed on the basis of the tight-form dynamic linearization， so that the improved model free adaptive iterative learning sliding mode control composite strategy can overcome the instability phenomenon and has strong robustness， thus further improving the system response speed and control accuracy. Finally， the control accuracy is stabilized within 1 μm by simulation and physical verification， and the accuracy and effectiveness of the proposed method is verified compared with other control schemes.

Keywords： improved model free adaptive iterative learning control; sliding mode control; two-dimensional linear motor; error rate of change; criterion function

0 引 "言

二维直线电机是一个具有强耦合、不确定性、多变量等特点的复杂控制对象[1]。随着智能制造，高端设备，自动控制技术的发展，二维直线电机的用途更加广泛。同时，也对二维直线电机的控制精度提出了更高的要求。其中基于二维直线电机的高速高精度运动平台是精密加工的核心部件，在精密加工技术领域，平台结构的运行精度和定位精度直接决定了工件的生产加工和量测精度。由于二维直线电机控制性能受系统不确定性的影响，例如参数变化、非线性摩擦、未知外部干扰、机械耦合、抖振等.因此提高直线电机的鲁棒性已成为当下研究和解决的问题之一[2]。

为达到期望的控制性能，解决传统控制器存在的问题，近年来提出了多种鲁棒控制器，如鲁棒补偿控制[3]、学习控制[4]、滑模控制[5-7]、神经网络控制[8]等。其中滑模控制因其对模型精度要求低、对外界干扰鲁棒性强而成为研究热点。滑模控制（sliding mode control， SMC）已成功应用于电机控制系统[6-7，9]。在文献[10]中，在电机闭环控制系统中应用滑模控制混合方法，结果表明所设计控制器的有效性是非常确定的。文献[8，11]为提高双直线电机系统跟踪精度，提出了将滑模控制和神经网络结合的方案，虽然保证了系统位置的跟踪性和鲁棒性，但是控制结构依然相对复杂。文献[12]为提高系统鲁棒性，提出了将自适应控制和模糊控制及扰动观测器相结合的控制策略来对永磁同步电机进行控制，结果表明，所设计的方案虽然具有较好的跟踪性能，改善了控制精度，但模糊规则的设计仍需要利用一定的先验知识。 文献[13]为减小双直线电机系统跟踪误差，提出了非奇异快速终端滑模控制，但所设计控制器对系统模型信息具有高度依赖性，不易实现。而相对于传统的无模型控制策略，虽无需建立直线电机动态模型，但控制效果往往难以达到要求，而基于模型的控制策略，所建模型精度对系统控制精度影响较大，控制律也较为复杂。针对以上问题，有学者提出了先进的无模型自适应控制（model free adaptive control， MFAC） [14-15]。文献[15]提出了鲁棒无模型自适应学习控制方案，建立一种基于伪偏导数（pseudo partial derivative，PPD）概念的无模型离散非线性系统建模方法。该方法中PPD的获取仅需要系统的输入输出数据，其控制器的设计也是仅依赖于系统的输入输出数据，该方法的提出在解决非线性系统建模困难的问题上提供了另一种思路。文献[16]针对非线性离散系统，提出了一种新的自适应准滑模控制策略，这种设计虽然是基于无模型设计的，但其没考虑系统不确定性带来的影响。在此基础上，文献[17]通过神经网络方法，解决系统不确定性带来的影响，提出了基于紧格式动态线性化方法（compact form dynamic linearization，CFDL）的神经网络滑模控制律使控制系统具有良好的稳定性和收敛性。因此，为减轻上述缺点，设计不依赖于精确数学模型且系统能稳定运行的控制方案，可以有效解决二维直线电机在实际运行过程中的问题。

针对以上问题，为进一步提高二维直线电机系统跟踪精度和控制性能，提出了将改进无模型自适应迭代学习控制（model free adaptive iterative learning control， MFAILC）与指数趋近律的滑模控制相结合的控制策略。一方面该控制策略无需二维直线电机系统精确数学模型，仅利用被控系统的输入输出数据，便可实现对严格重复运作的系统在有限区间上的完全跟踪和稳定精密控制；另一方面利用滑模动态的优势，进一步提高系统收敛速度和跟踪性能，较单独作用的无模型自适应迭代学习控制或滑模控制，该控制方案对外界干扰具有较强的抵抗能力，且具有在线学习功能，调节参数少，降低了控制难度，增强了系统鲁棒性，加快了学习收敛速度，并保证了系统稳定收敛。最后通过仿真和实验对改进MFAILC-SMC复合策略进行有效验证。

1.1 二维直线电机简化模型辨识

在建立二维直线电机数学模型之前，做以下假设。①忽略直线电机的端部效应及铁心饱和效果；②磁场均匀分布；③三项绕组分布均匀对称；④忽略涡流和磁滞损耗[10，13]。

基于二维直线电机运动控制系统实物平台，在建立其数学模型时需要考虑诸多外部干扰和不确定性[2]，其中主要是耦合作用力、电磁推力、非线性摩擦力等[9-10]。依据二维直线电机动力学特性，通过建模和简化[1]，二维直线电机平台数学模型可简化表示为：

仿真分析与实验验证

2.1 仿真

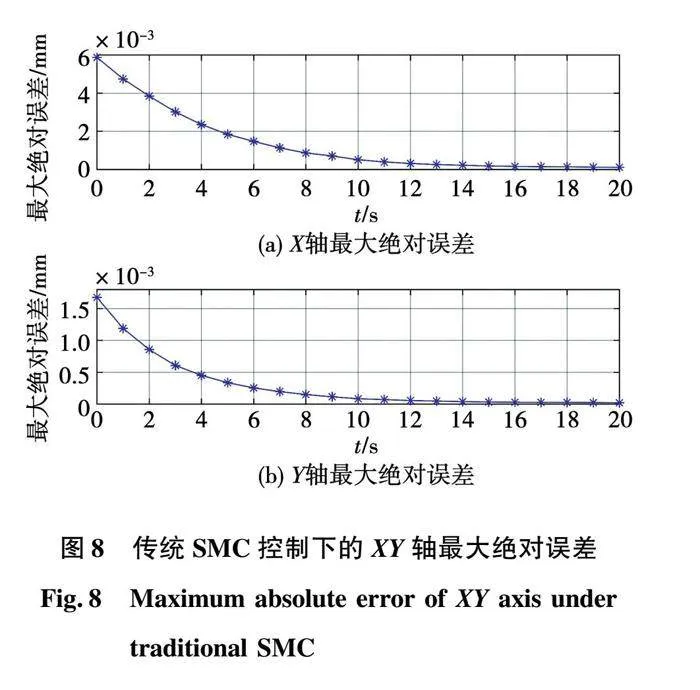
利用设计的控制算法，首先在MATLAB中进行仿真，然后在Rt-Sim半实物仿真平台上进行验证。给定时间区间为20s，参数设置：迭代学习控制律采用PD型，迭代前馈输入为： ，X轴： ，Y轴： ， 给定XY轴期望为周期为1s，采样时间为0.01s，幅值为0.03m的正余弦信号。仿真结果如图5-7：迭代次数为动态变化，随着迭代次数增加，跟踪误差在16次之后无明显变化，因此选迭代次数为20次做分析。MATLAB仿真结果如图8所示：

图5为迭代稳定时XY轴跟踪误差，跟踪误差在一定范围内波动，验证了算法的有效性：尽管时间轴是变化的，但跟踪误差仍沿迭代轴收敛。

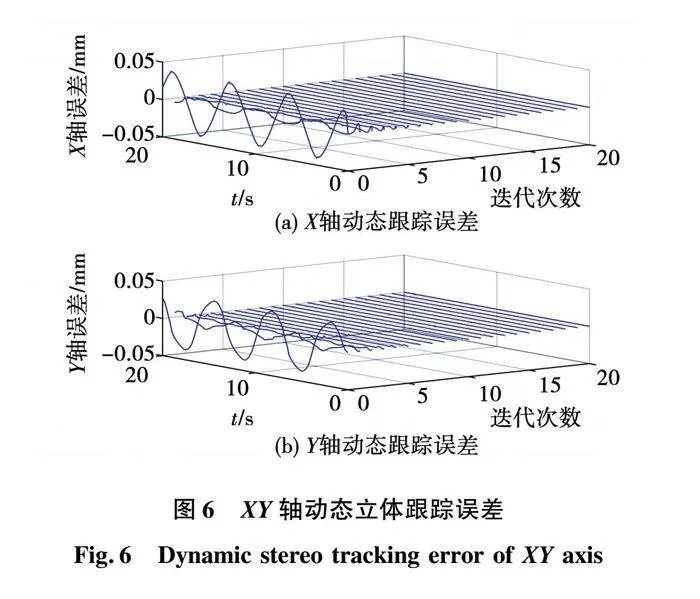
从图6至图7可以看出，跟踪效果随着时间轴和迭代轴的变化而变化。随着迭代次数和采样时间的增加，跟踪误差趋于稳定。

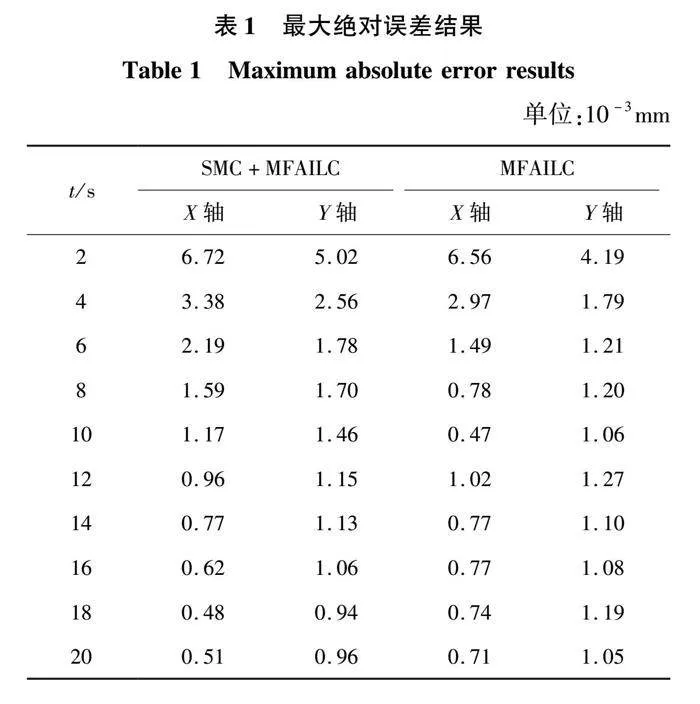
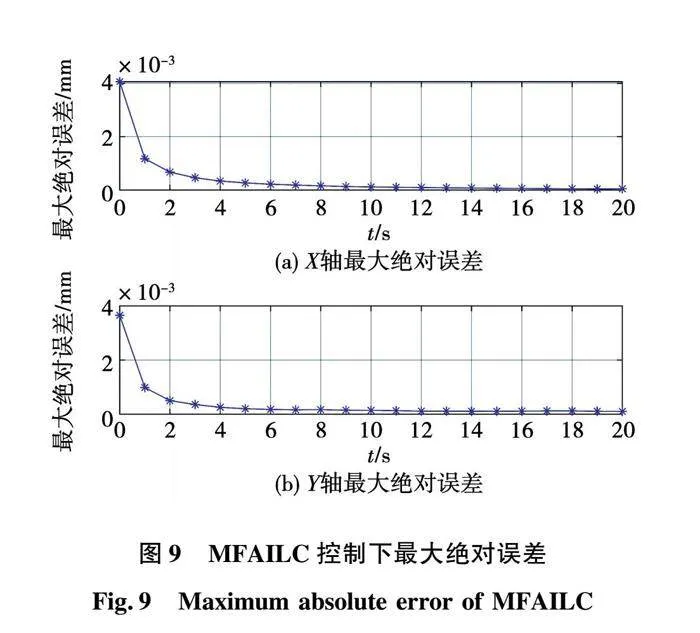
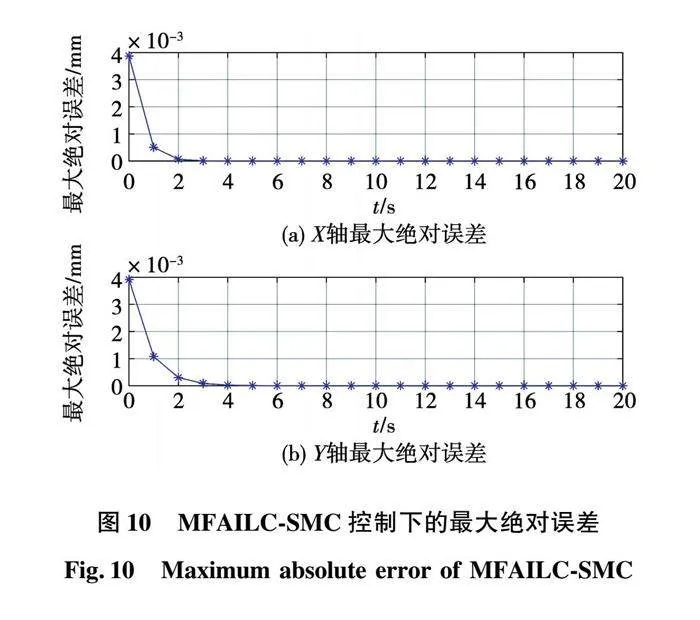
由仿真结果可见，图8至图10为不同控策略下的最大绝对误差。若存在参数设定值改变情况下，三种控制算法均获得满意的控制效果。从图10与图8可以看出，系统到达稳定状态的时间明显缩短，加快了收敛速度；从图10和图9可以看出，XY轴最大绝对误差明显减小，同时，MFAILC-SMC的收敛速度也明显优于MFAILC和SMC单独作用时的动态性能。从表1数据更加明显得出加入SMC之后的MFAILC的控制算法优于单独MFAILC算法，验证了所提算法的可行性。

2.2 实物验证

在RT-Sim半实物仿真平台上进行实物验证.参数设置与仿真参数设置相同，同时选取迭代次数为20次，初始参数不变，期望为正弦信号，幅值设为0.03m，周期为1s，t为采样时刻，采样时间间隔为0.01s。

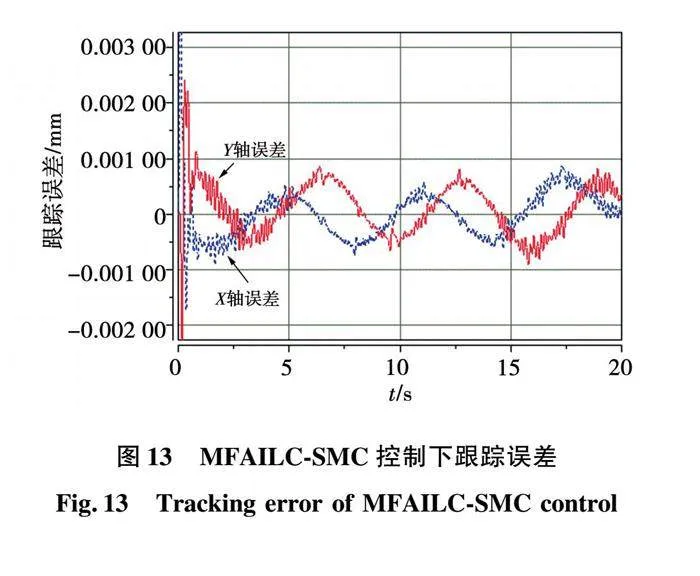
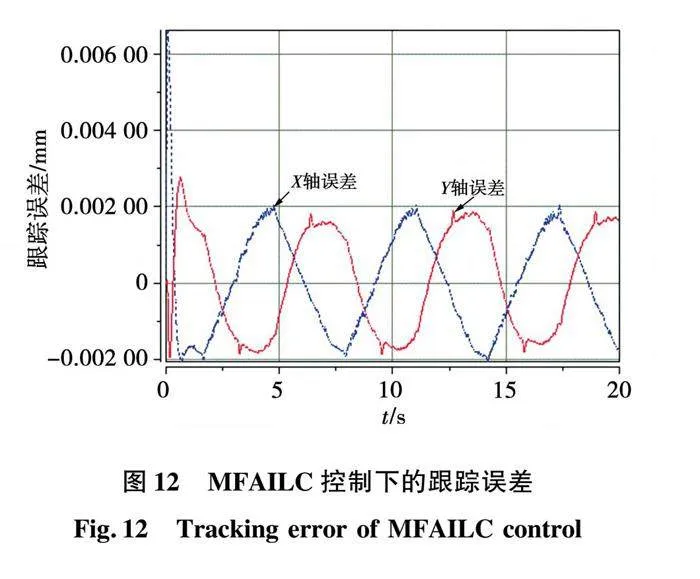
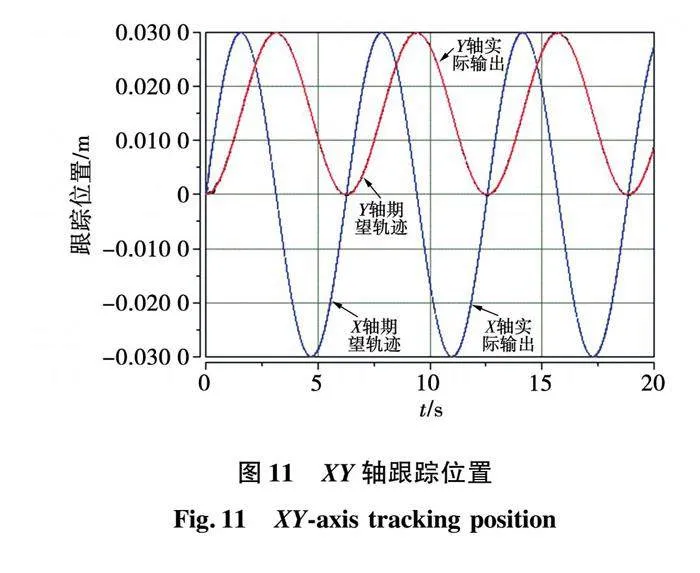
从11可以看出，直线电机的实际位置输出曲线可以和期望轨迹曲线很好的拟合。在传统SMC控制算法下的参数设置和在MFAILC-SMC控制算法下的参数设置可以保持不变，系统具有较强的鲁棒性。从图12至图13可以看出，迭代次数的增加，直线电机的跟踪误差逐步减小，迭代16次以后，MFAILC控制精度稳定在 范围内；MFAILC-SMC控制精度稳定在 范围内，验证了所提方案的有效性。

同时，与其他控制方案相比[22-23]，文献[22]双轴跟踪误差稳定在 ；文献[23]迭代次数在达到80次时，直线电机的位置误差稳定在 左右。从图7和图13可以看出MFAILC-SMC控制策略迭代次数和跟踪误差都有所降低，综合可见，本文所提MFAILC-SMC控制方案具有良好的跟踪性能，从而验证了所提控制策略的优越性。

3 结论

本文提出了一种基于改进无模型自适应迭代学习的滑模控制复合策略，首先在MFAILC准则函数中加入对跟踪误差变化率的限制因子，然后在改进紧格式动态线性化MFAILC基础上设计了新型滑模控制律，形成了复合MFAILC控制算法。改进的MFAILC-SMC可以显著减小系统跟踪误差，克服控制过程中的不稳定现象，同时提高系统跟踪精度和响应速度，增强系统鲁棒性，优于单独作用于二维直线电机传统控制等方法，并对其收敛性进行分析论证。仿真和实验结果表明，所提方案可将跟踪误差精度稳定的控制在一定范围内，降低系统状态受参数变化的约束和外部扰动的影响，并保证系统的收敛性，减小位置跟踪误差，提高了被控系统的整体动态控制性能。

参 考 文 献：

[1] 曾子强，曹荣敏，侯忠生，等.二维直线电机的多入多出无模型自适应轮廓控制[J].控制理论与应用，2020，37（5）：1007.

ZENG Ziqiang， CAO Rongmin， HOU Zhongsheng， et al. Multiple input multiple output model free adaptive contour control for two-dimensional linear motors[J].Control Theory and Applications，2020，37（5）：1007.

[2] WANG Yaoqiang， FENG Yutao， ZHANG Xiaoguang， et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system[J].IEEE Transactions on Power Electronics， 2020，35（4）. 4117.

[3] 武志涛，杨兆宁.永磁直线同步电机的双闭环鲁棒补偿控制[J].电机与控制学报，2022，26（3）：102.

WU Zhitao， YANG Zhaoning. Double closed-loop robust compensation control for permanent magnet linear synchronous motors [J]. Electric Machines and Control，2022，26（3）：102.

[4] 张康，王丽梅.基于周期性扰动学习的永磁直线电机自适应滑模位置控制[J].电机与控制学报，2021，25（8）：135.

ZHANG Kang， WANG Limei. Adaptive sliding mode position control for permanent magnet linear motor based on periodic disturbance learning[J]. Electric Machines and Control，2021，25（8）：135.

[5] 东野亚兰，杨淑英，王奇帅，等.基于增强型扩张状态观测器的永磁同步电机低抖振高抗扰二阶终端滑模电流控制[J].电工技术学报，2024，39（8）：2440.

DONGYE Yalan， YANG Shuying， WANG Qishuai， et al. Enhanced extended state observer based second order terminal sliding mode current control for permanent magnet synchronous machine with low chattering and improved disturbance rejection [J]. Transactions of China Electrotechnical Society，2024，39（8）：2440.

[6] 赵希梅，孙洪潇，金鸿雁.永磁直线伺服系统终端互补滑模位置控制[J].电机与控制学报，2023，27（6）：183.

ZHAO Ximei， SUN Hongxia， JIN Hongyan. Terminal complementary sliding mode position control for permanent magnet linear servo system[J]. Electric Machines and Control，2023，27（6）：183

[7] 康尔良，蔡松昌.永磁同步电机自构式模糊神经网络控制器设计[J].电机与控制学报，2023，27（3）：95.

KANG Erliang， CAI Songchang. Design of self-constructing fuzzy neural network controller for permanent magnet synchronous motor[J]. Electric Machines and Control，2023，27（3）：95.

[8] 李耀华，赵承辉，周逸凡等.基于数据驱动的永磁同步电机深度神经网络控制[J].电机与控制学报，2022，26（1）：118.

LI Yaohua， ZHAO Shenghui， ZHOU Yifan， et al. Deep neural network control for PMSM based on data drive [J]. Electric Machines and Control，2022，26（1）：118.

[9] ZHANG Xiaoguang， HOU Benshuai， MEI Yang. Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer[J]. IEEE Transactions on Power Electronics， 2017，32（5）： 3820.

[10] JIANG Yajie， WEI Xu， MU Chaoxu， et al. Improved deadbeat predictive current control combined sliding mode strategy for PMSM drive system[J]. IEEE Transactions on Vehicular Technology，2018，67（1）：258.

[11] 王天鹤，赵希梅，金鸿雁.基于递归径向基神经网络的永磁直线同步电机智能二阶滑模控制[J].电工技术学报，2021，36（6）：1233.

WANG Tianhe， ZHAO Ximei， JIN Hongyan. Intelligent second-order sliding mode control based on recurrent radial basis function neural network for permanent magnet linear synchronous motor [J]. Transactions of China Electrotechnical Society， 2021，36 （6）： 1233.

[12] 赵希梅，王浩林，朱文彬.基于自适应模糊控制器和非线性扰动观测器的永磁直线同步电机反馈线性化控制[J].控制理论与应用，2021，38（5）：599.

ZHAO Ximei， WANG Haolin， ZHU Wenbin. Feedback linearization control of permanent magnet linear synchronous motor based on adaptive fuzzy controller and nonlinear disturbance observer [J]. Control Theory and Applications，2021，38（5）：599.

[13] 苏普春，王丽梅.直驱H型平台的非奇异快速终端滑模同步控制[J].组合机床与自动化加工技术，2020，（11）：73.

SU Puchun， WANG Limei. Non-singular fast terminal sliding mode synchronous control for direct drive H-type platform [J]. Modular Machine Tool amp;Automatic Manufacturing Technique，2020（11）：73.

[14] HOU Zhongsheng， JIN Shantai. Model free adaptive control-theory and applications[M]. Boca Raton： CRC Press， 2013.

[15] 侯忠生，韩志刚.非线性系统鲁棒无模型学习自适应控制[J].控制与决策，1995（2）：139.

HOU Zhongsheng， HAN Zhigang. Robust model-free learning adaptive control for nonlinear systems [J]. Control and Decision，1995（2）：139.

[16] 侯忠生， 金尚泰. 无模型自适应控制：理论与应用[M]. 北京： 科学出版社， 2013.

[17] 侯忠生， 王卫红， 金尚泰. 一类非线性离散系统自适应准滑模控制[J]. 控制理论与应用， 2009， 26（5）： 507.

HOU Zhongsheng， WANG Weihong， JIN Shangtai. Adaptive quasi-sliding-mode control for a class of nonlinear discrete-time systems [J]. Control Theory amp; Applications， 2009， 26（5）： 507.

[18] LIN Na， LI Huaying， CHI Ronghu， et al. Data-driven virtual reference set-point learning of PD control and applications to permanent magnet linear motors[J]. IEEE Transactions on Systems， Man， and Cybernetics： Systems，2023，53（7）： 4149.

[19] LIU Tong， HOU Zhongsheng. Model-free adaptive containment control for unknown multi-input multi-output nonlinear MASs with output saturation[J]. IEEE Transactions on Circuits and Systems I： Regular Papers，2023，70（5）： 2160.

[20] 王要强，朱亚昌，冯玉涛，等.永磁同步电机新型趋近律滑模控制策略[J].电力自动化设备，2021，41（1）：195.

WANG Yaoqiang， ZHU Yachang， FENG Yutao， et al. New reaching law sliding mode control strategy for permanent magnet synchronous motor [J]. Power Automation Equipment，2021，41（1）：195.

[21] SHAO Ke， ZHENG Jinchuan， HUANG Kang， et al. Finite-time control of a linear motor positioner using adaptive recursive terminal sliding mode[J]. IEEE Transactions on Industrial Electronics， 2019， 67（8）： 6661.

[22] 王丽梅，郝中扬，方馨，等.基于自抗扰的H型平台模糊神经网络同步控制[J].电气工程学报，2022，17（3）：125.

WANG Limei， HAO Zhongyang， FANG Xin， et al. Fuzzy neural network synchronous control of H-type platform based on active disturbance rejection [J]. Journal of Electrical Engineering，2022，17（3）：125.

[23] 赵云杰，曹荣敏，周惠兴. 非圆车削系统的无模型自适应迭代学习控制[J].控制工程，2018，25（10）：1925.

ZHAO Yunjie， CAO Rongmin， HOU Zhongsheng. Model-free adaptive iterative learning control for noncircular turning system [J]. Control Engineering，2018，25（10）：1925.

（编辑：刘素菊）