倍压整流型LCC谐振变换器轨迹控制启动策略

摘 "要：倍压整流型LCC谐振变换器兼顾了串联和并联谐振变换器的优点，具有高电压增益、抗负载短路、兼容变压器寄生参数等能力，已成为医用X光机高压发生器的优选拓扑。然而，倍压整流器中的电容参与谐振、增加谐振元件数量，导致变换器的动态特性更复杂，进而对建模和控制提出更高的要求。传统的基波近似法和线性控制难以实现精确建模并跟踪控制指标。对此，该文采用状态平面分析法，通过分析变换器的工作原理，建立各模态归一化状态轨迹方程。在此基础上，提出一种状态轨迹控制启动策略，该策略通过设置谐振电流限幅值，根据输出电压变化规划最优路径，使状态变量在最短时间内跟踪谐振腔最优轨迹，以此计算最佳开关频率。最后，在50kW/140kV的样机上验证所提建模方法的准确性和控制策略有效性。实验结果表明，与传统控制相比，所提方法有效提升了启动速度、实现了不同电压等级之间的快速切换，抑制了谐振腔电流、电压过冲。

关键词：LCC谐振变换器；倍压整流；高压发生器；状态平面分析；状态轨迹方程；启动策略

DOI：

中图分类号：TM46 " " " " " " 文献标志码：A " " " " " "文章编号：

Trajectory control based startup strategy for LCC resonant converter with voltage-doubling rectifier

ZHANG Shanlu1， ZHAO Zhennan1， LI Lei1， FANG Shengfang2， WANG Cheng1

（1. School of Automation， Nanjing University of Science and Technology， Nanjing 210094， China;

2. Powersit Electric Co.， Ltd.， Suzhou 215163， China）

Abstract： The LCC resonant converter integrating voltage-doubling rectifier takes into account the advantages of series and parallel resonant converters. It has become the preferred topology for high-voltage generator for medical X-ray machines， due to the benefits like high voltage gain， anti-load short-circuit， compatibility with transformer parasitic parameters， etc. However， the rectifier capacitors participate in the resonance and increase the number of resonant components， which leads to more complex dynamic characteristics of the converter， which in turn puts forward higher requirements for modeling and control. The conventional fundamental harmonic approximation and linear control are difficult to achieve accurate modeling and track control indicators. To address this， the state plane analysis method is adopted. The normalized state trajectory equation of each mode is established by analyzing the working principle of the converter. On this basis， a state trajectory control strategy of startup is proposed. By setting the limit value of the resonant current and sensing the output voltage， the state variable can track the optimal trajectory of the resonant tank in the shortest time. The optimal switching frequency can then be derived. Finally， the accuracy of the proposed modeling method and the effectiveness of the control strategy are verified on a 50kW/140kV prototype. The experimental results show that， compared with the conventional control， the proposed methods effectively improve the startup speed， realize fast switching between different voltage levels， and suppress the resonator current and voltage overshoot.

Keywords： LCC resonant converter; voltage-doubling rectifier ; high voltage generator; state plane analysis; state trajectory equation; startup strategy

0 引 "言

高压直流电源（high voltage power supplies，HVPS）已经广泛应用于医用X光机、静电除尘、电容充电器、电子束焊接以及粒子加速器等领域[1-5]。针对不同应用领域，对输出电压和输出功率等规格的要求也是不尽相同。用于医疗诊断的计算机断层扫描设备（computerized tomography，CT）的高压直流电源需要上百千伏的高电压和几十千瓦的高功率来驱动X射线球管。通常输出电压范围为40～150kV，输出电流范围为0.5～1000mA。针对人体不同的诊断部位，可选择透视模式或照相模式[6]。随着医疗CT的发展，双能CT凭借成本低和成像质量高的优势已成为国内外研究的热点。由于只使用一套高压电源来实现不同kV电压等级在一个X射线球管之间的快速切换，因此对切换速度有更高的要求，如果能将切换速度控制在100～200μs以内，对于医疗CT的发展将有重要价值和意义[7-12]。

高压发生器作为X光机高压电源的核心部件，直接影响系统性能。医用CT设备中的X光机高压发生器系统主要由灯丝电源和高压电源组成。LCC谐振变换器兼顾串联和并联谐振变换器的优点，同时又具有高电压增益和兼容变压器寄生参数的特点，目前已成为医用X光机高压电源的优选拓扑。因此，国内外学者在LCC谐振变换器建模方法、控制策略等方面也展开了一系列研究。文献[13]提出基波等效法实现了对具有电感输出滤波器的谐振变换器的建模，由于只考虑基波成分，建模精度较低。为提高建模精度，文献[14]提出一种改进的基波近似法，在原基波等效电路中并联一个滤波电感，考虑纹波电流使参数设计更加准确。对具有电容输出滤波器的LCC谐振变换器，文献[15]利用基波近似法，提出一种新的RC等效模型，可以得到输出电压增益特性与开关频率、负载变化的关系，为谐振参数优化提供了依据。文献[16]提出时域建模法，但计算复杂，且只能获得数值解，很难得到输出特性表达式。文献[17]提出一种分段线性化解析模型，基于状态空间法对每个工作模态求解，从而推导出稳态模型。进一步地，文献[18]提出用状态平面分析法建立谐振变换器的动态特性模型，并提出了轨迹控制策略，取得了良好的效果。此后，该方法在LLC谐振变换器的轻载Burst模式、软启动及短路保护中迅速得到了应用[19-21]。

对于LCC谐振变换器，文献[22-23]提出轨迹控制，实现了稳态控制以及稳态之间的平滑切换。文献[24]基于平面轨迹提出电流连续和断续之间多模式切换的恒功率充电器，充电效率提高但是控制十分复杂。文献[25-26]提出电流断续模式下基于临界模态的归一化建模方法及轨迹控制策略，简化了谐振参数的设计，但是开关频率较低不适用于高压大功率场合。文献[27]提出基于轨迹控制的两点求解法，实现了快速求解稳态轨迹参数的目标，提高了动态响应速度，但是对硬件配置要求较高。以上文献都是基于全桥整流电路的LCC谐振变换器展开的研究，对具有倍压整流型的LCC谐振变换器结构研究较少。原因是倍压整流器在导通过程中其倍压电容参与谐振，谐振腔由三元件变成五元件谐振，导致变换器的动态特性更复杂，使其建模和控制更加困难。

综上所述，针对倍压整流型的LCC谐振变换器的轨迹控制国内外研究较为鲜见。本文首先采用状态平面分析法，对每个模态建立二维平面内的归一化状态轨迹方程。基于时域模型提出一种状态轨迹控制启动策略，通过规划最优轨迹路径对启动过程进行了详细的理论推导和计算。最后，实验结果对所提出建模方法和控制策略进行了充分的验证。

1.1 拓扑结构

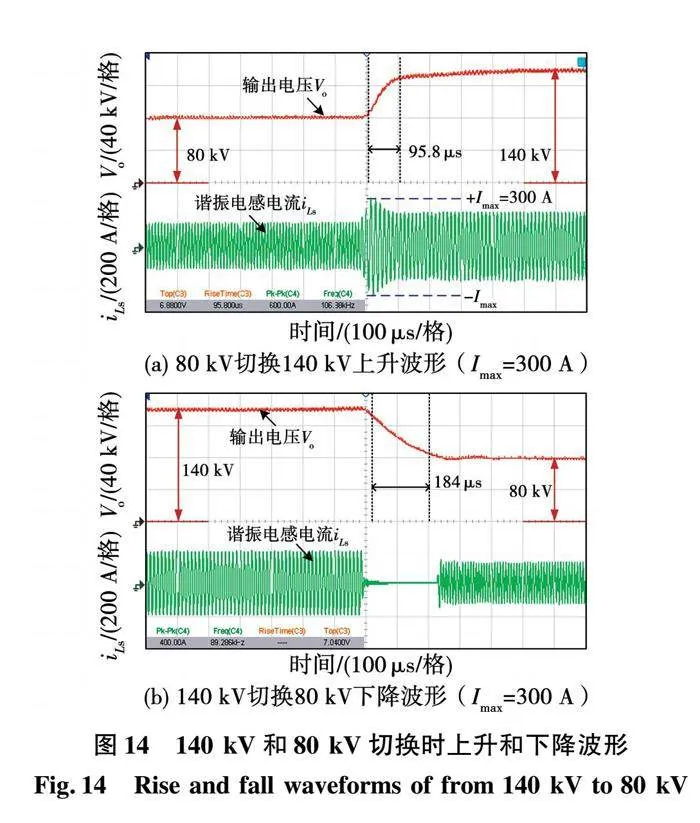
倍压整流型LCC谐振变换器拓扑如图1所示，逆变桥由S1、S2、S3和S4组成，变压器电压比为1：n，谐振腔由Ls、Cs和Cp构成，其中Cp为高压变压器二次绕组的寄生电容折算到一次侧后的等效电容值。与全桥整流电路不同，变压器二次侧输出端使用了电压倍增电路，根据输出电压要求，可设置多组串联输出（m=1，3，5…），目的是减小变压器电压比，降低寄生电容的影响以及减小倍压整流二极管电气应力。

为简化电路分析，此处选择一级倍压电路进行建模，忽略变压器结构，且Cr1=Cr2=Cr。同时假设所有器件均为理想的，输出滤波电容Cf足够大，忽略输出电压的纹波，X射线管用电阻RL替代。简化等效电路结构如图2所示。

1.2 状态平面建模

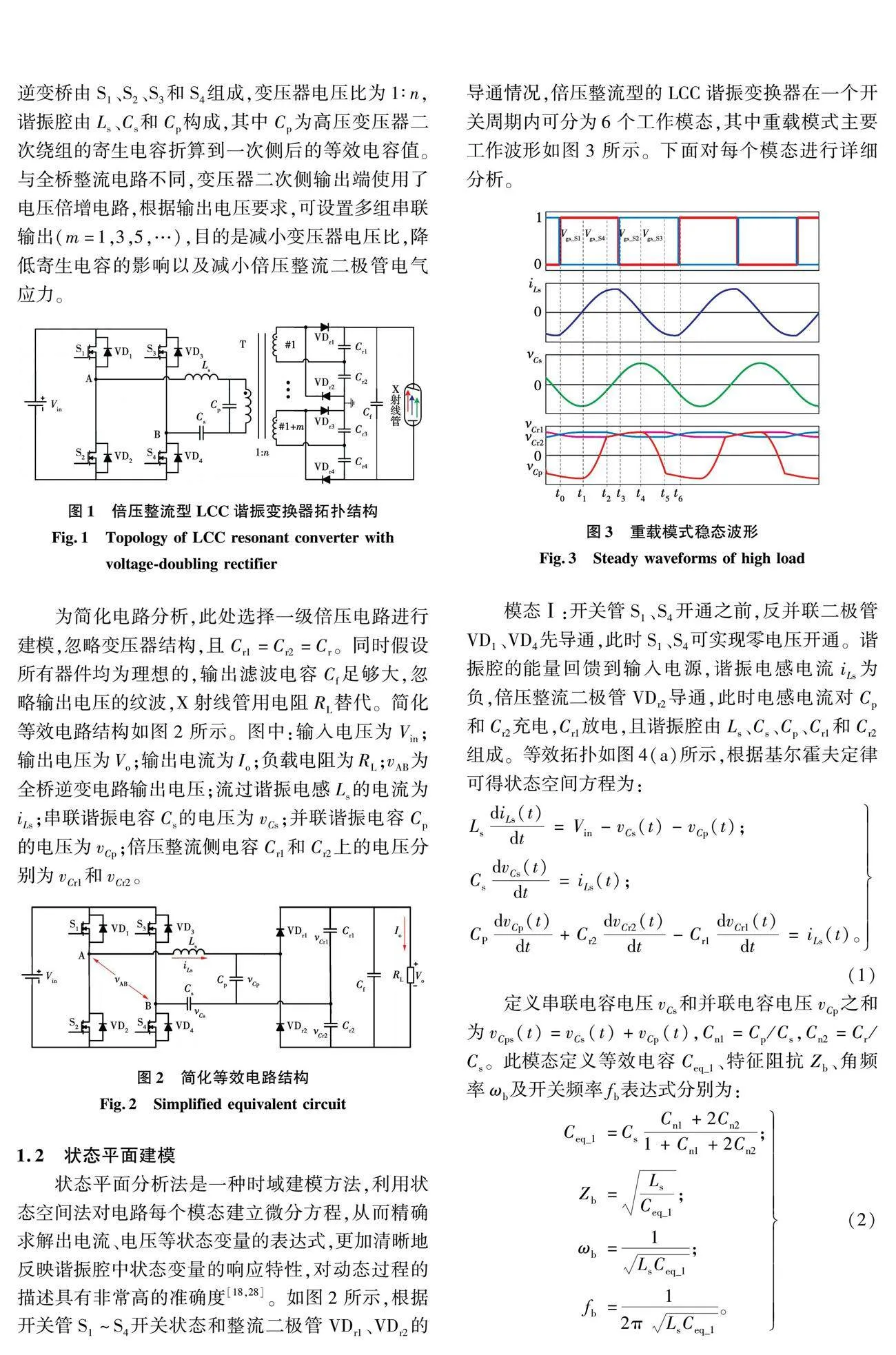
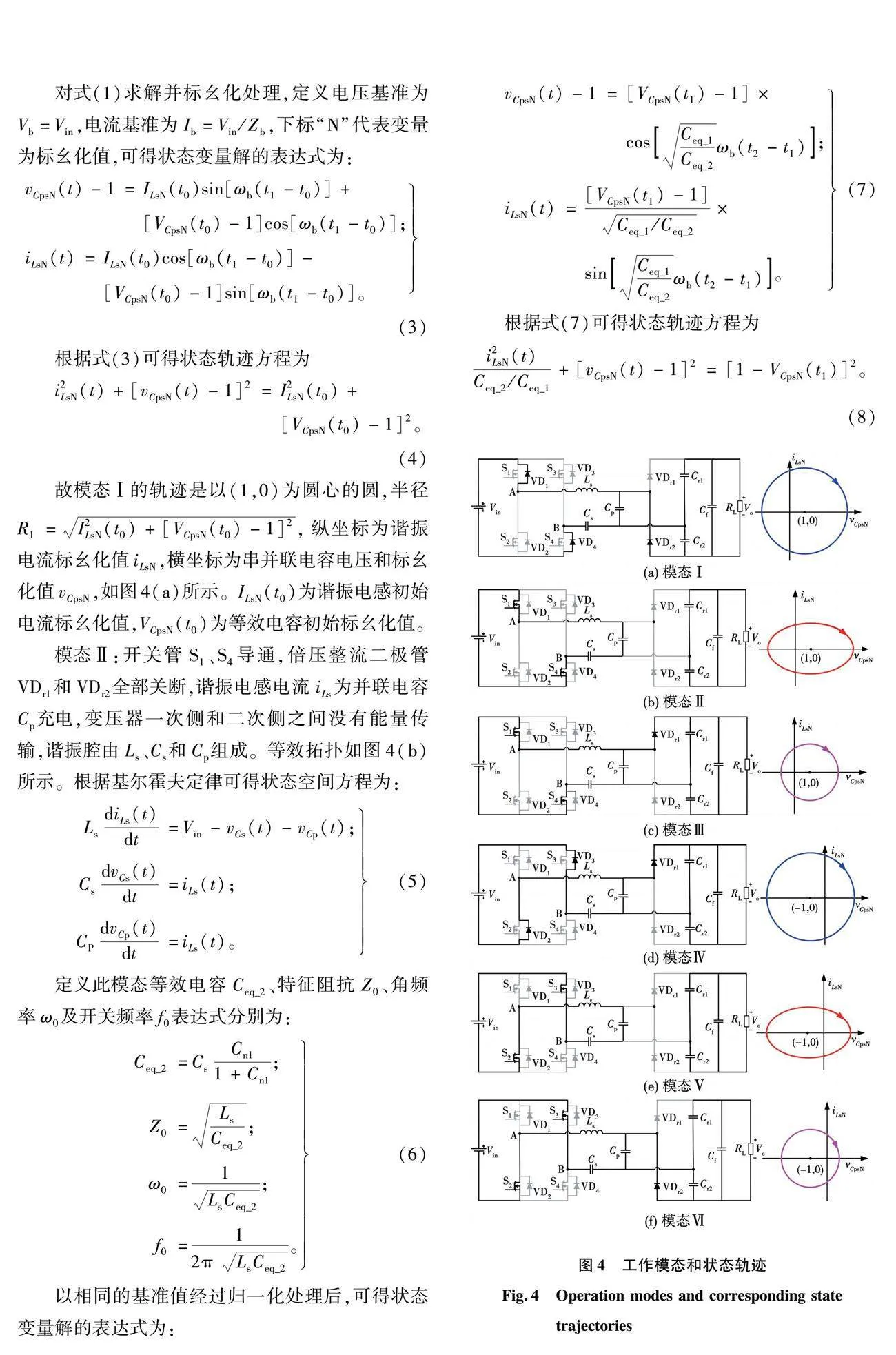
状态平面分析法是一种时域建模方法，它利用状态空间法对电路每个模态建立微分方程，从而精确求解出电流、电压等状态变量的表达式，更加清晰的反映谐振腔中状态变量的响应特性，对动态过程的描述具有非常高的准确度[18，28]。如图2所示，根据开关管S1～S4开关状态和整流二极管VDr1、VDr2的导通情况，倍压整流型的LCC谐振变换器在一个开关周期内可分为六个工作模态，其中重载模式主要工作波形如图3所示。

图2中：输入电压为Vin；输出电压为Vo；输出电流为Io；负载电阻为RL；vAB为全桥逆变电路输出电压；流过谐振电感Ls的电流为iLs；串联谐振电容Cs的电压为vCs；并联谐振电容Cp的电压为vCp；倍压整流侧电容Cr1和Cr2上的电压分别为vCr1和vCr2。下面对每个模态进行详细分析。

模态Ⅰ：开关管S1、S4开通之前，反并联二极管VD1、VD4先导通，此时S1、S4可实现零电压开通。谐振腔的能量回馈到输入电源，谐振电感电流iLs为负，倍压整流二极管VDr2导通，此时电感电流对Cp和Cr2充电，Cr1放电。且谐振腔由Ls、Cs、Cp、Cr1和Cr2组成。等效拓扑如图4（a）所示，根据基尔霍夫定律可得状态空间方程为：

等效拓扑电路和轨迹如图4（d）～图4（f）所示。因此，倍压整流型LCC谐振变换器的工作模态由上述6种基本模态构成，其对应的状态轨迹最多由六段不同的圆弧组合而成。无论工作在何种模式工况下，均可以由该基本模态的轨迹进行描述。

为分析启动过程的暂态状态轨迹，首先可以根据稳态基波等效法得到直流电压特性增益与开关频率关系，如图5所示。

根据谐振电流是否连续分为电流连续模式（continuous current mode，CCM）和电流断续模式（discontinuous current mode，DCM），DCM具有开关频率低，动态响应较慢，开关管电流应力过大等问题，而CCM 模式开关频率较高响应速度快。图5中虚线代表纯阻性负载曲线，是实现开关管零电流关断（zero current switching， ZCS）和零电压开通（zero voltage switching， ZVS）分界线，fp为同一负载下的峰值电压增益对应的归一化频率。针对医用X光机高压电源，为实现软开关，通常要求工作于CCM模式下的ZVS区，即满足归一化频率fngt;fp。

2 轨迹控制启动策略分析

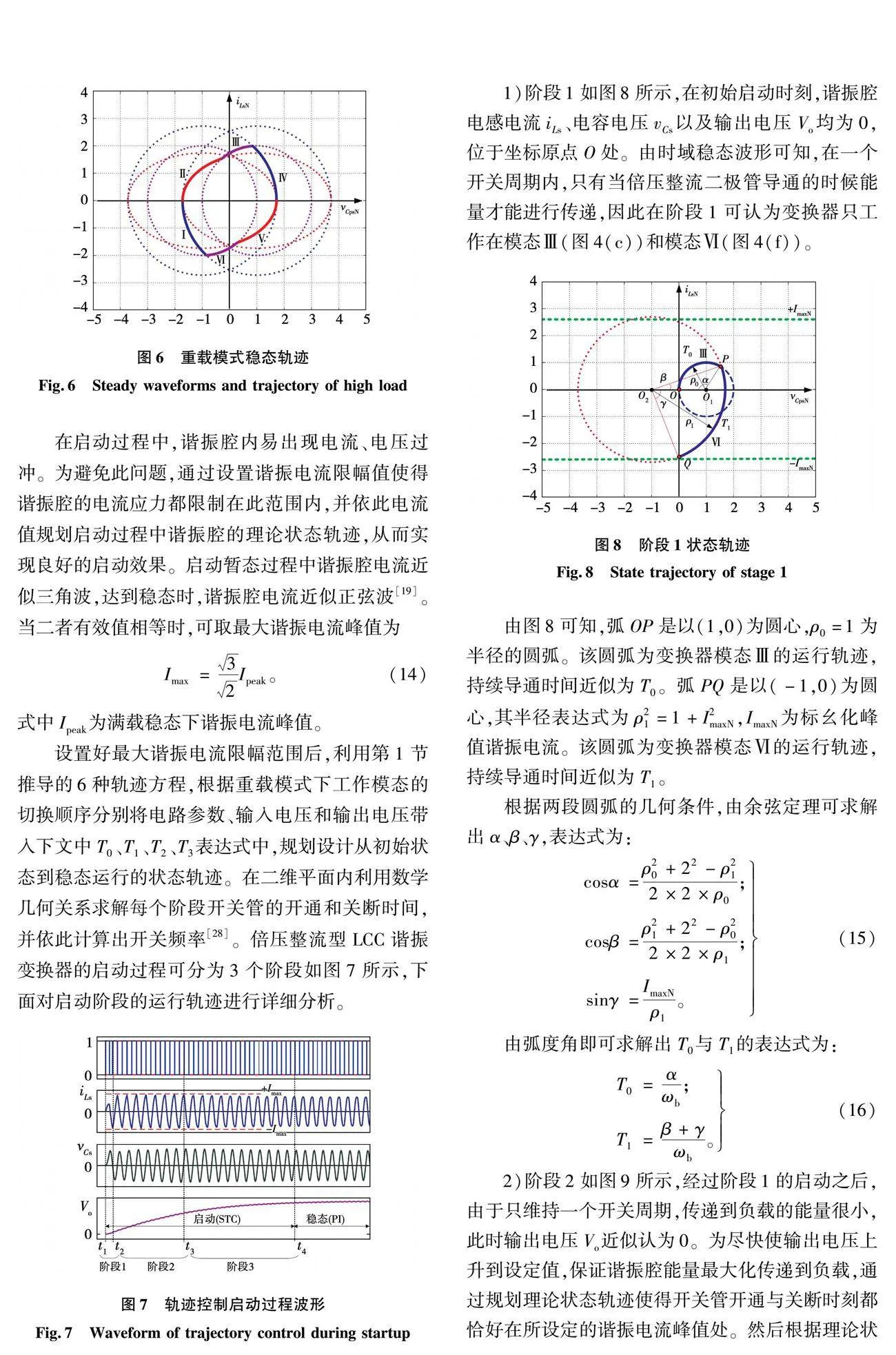
对于医用X光机CT高压电源，输出电压的上升时间是衡量系统性能的主要指标，此时间段内X射线对人体产生无效辐射，因此要求输出电压的启动速度越快越好[1，6]。而额定功率重载模式下的启动时间又是决定系统启动速度的关键，所以文中主要解决的是重载模式下的启动问题。重载模式下的轨迹如图6所示。基于第1节所建立的状态平面时域轨迹模型，提出一种基于状态轨迹控制的启动策略，通过设置谐振电流最大限幅范围，规划启动过程中不同阶段的理论状态轨迹，进而推导计算出最优开关频率，以更精确的分段控制获得较快的启动速度。

在启动过程中，谐振腔内易出现电流、电压过冲。为避免此问题通过设置谐振电流限幅值，使得谐振腔的电流应力都限制在此范围内，并依此电流值规划启动过程中谐振腔的理论状态轨迹，从而实现良好的启动效果。启动暂态过程中谐振腔电流近似三角波。达到稳态时，谐振腔电流近似正弦波[19]。当二者有效值相等时，可取最大谐振电流峰值为

（14）

式中Ipeak为满载稳态下谐振电流峰值。

设置好最大谐振电流限幅范围后，利用第1节推导的6种轨迹方程，根据重载模式下工作模态的切换顺序分别将电路参数、输入电压和输出电压带入下文中T0、T1、T2、T3表达式中，规划设计从初始状态到稳态运行的状态轨迹。在二维平面内利用数学几何关系求解每个阶段开关管的开通和关断时间，并依此计算出开关频率[28]。倍压整流型LCC谐振变换器的启动过程可分为3个阶段如图7所示，下面对启动阶段的运行轨迹进行详细分析。

阶段1：如图8所示，在初始启动时刻，谐振腔电感电流iLs、电容电压vCs以及输出电压Vo均为0，位于坐标原点O处。由时域稳态波形可知，在一个开关周期内，只有当倍压整流二极管导通的时候能量才能进行传递，因此在阶段1可认为变换器只工作在模态Ⅲ（图4（c））和模态Ⅵ（图4（f））。

由图8可知，弧OP是以（1，0）为圆心，ρ0=1为半径的圆弧。该圆弧为变换器模态Ⅲ的运行轨迹，持续导通时间近似为T0。弧PQ是以（-1，0）为圆心，其半径表达式为ρ12=1+I2maxN。ImaxN为标幺化峰值谐振电流。该圆弧为变换器模态Ⅵ的运行轨迹，持续导通时间近似为T1。

根据两段圆弧的几何条件，由余弦定理可求解出α、β、γ，表达式为：

（15）

由弧度角即可求解出T0与T1的表达式为：

（16）

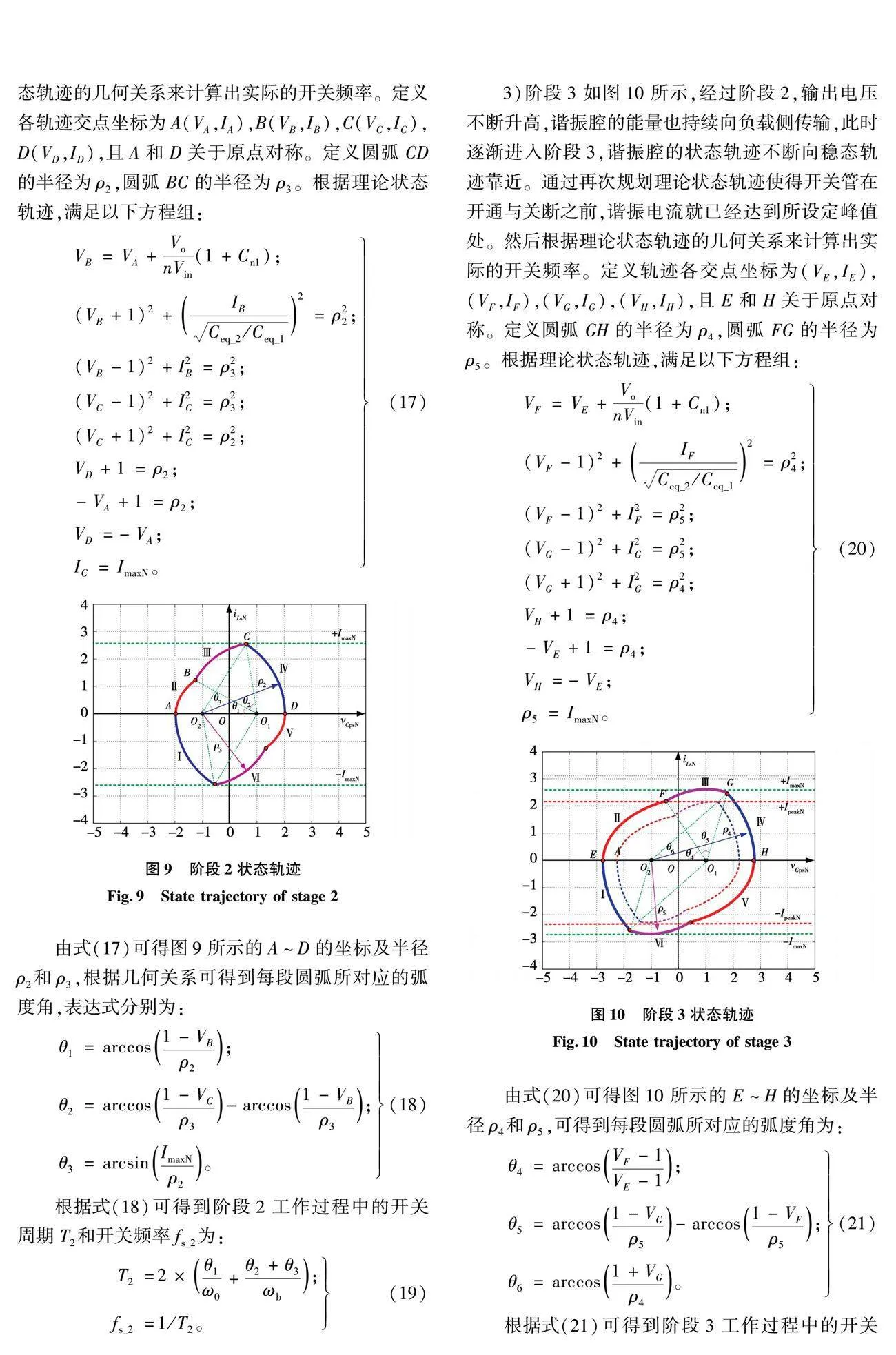
阶段2：如图9所示，经过阶段1的启动之后，由于只维持一个开关周期，传递到负载的能量很小，此时输出电压Vo近似认为0。为尽快使输出电压上升到设定值，保证谐振腔能量最大化传递到负载，通过规划理论状态轨迹使得开关管开通与关断时刻都恰好在所设定的谐振电流峰值处。然后根据理论状态轨迹的几何关系来计算出实际的开关频率。定义各轨迹交点坐标为A（VA，IA），B（VB，IB），C（VC，IC），D（VD，ID），且A和D关于原点对称。定义圆弧CD的半径为ρ2，圆弧BC的半径为ρ3。根据理论状态轨迹，满足以下方程组：

（17）

由式（17）可得图9所示的A～D的坐标及半径ρ2和ρ3，根据几何关系可得到每段圆弧所对应的弧度角，表达式分别为：

（18）

根据式（18）可得到阶段2工作过程中的开关周期T2和开关频率fs_2为：

（19）

阶段3：如图10所示，经过阶段2，输出电压不断升高，谐振腔的能量也持续向负载侧传输，此时逐渐进入阶段3，谐振腔的状态轨迹不断向稳态轨迹靠近。通过再次规划理论状态轨迹使得开关管在开通与关断之前，谐振电流就已经达到所设定峰值处。然后根据理论状态轨迹的几何关系来计算出实际的开关频率。定义轨迹各交点坐标为（VE，IE），（VF，IF），（VG，IG），（VH，IH），且E和H关于原点对称。定义圆弧GH的半径为ρ4，圆弧FG的半径为ρ5。根据理论状态轨迹，满足以下方程组：

（20）

由式（20）可得图10所示的E～H的坐标及半径ρ4和ρ5，可得到每段圆弧所对应的弧度角为：

（21）

根据式（21）可得到阶段3工作过程中的开关周期T3和开关频率fs_3为：

（22）

至此，完成启动过程的三个阶段的详细分析。待阶段3末期时，输出电压基本接近参考电压，此时将谐振电流峰值ImaxN逐渐减小到稳态谐振电流值IpeakN，重复阶段3的计算方法直至变换器完全进入稳态，如图10虚线轨迹所示。进入稳态后系统切换到PI控制，消除静态误差，实现零静差跟踪。

3 实验验证

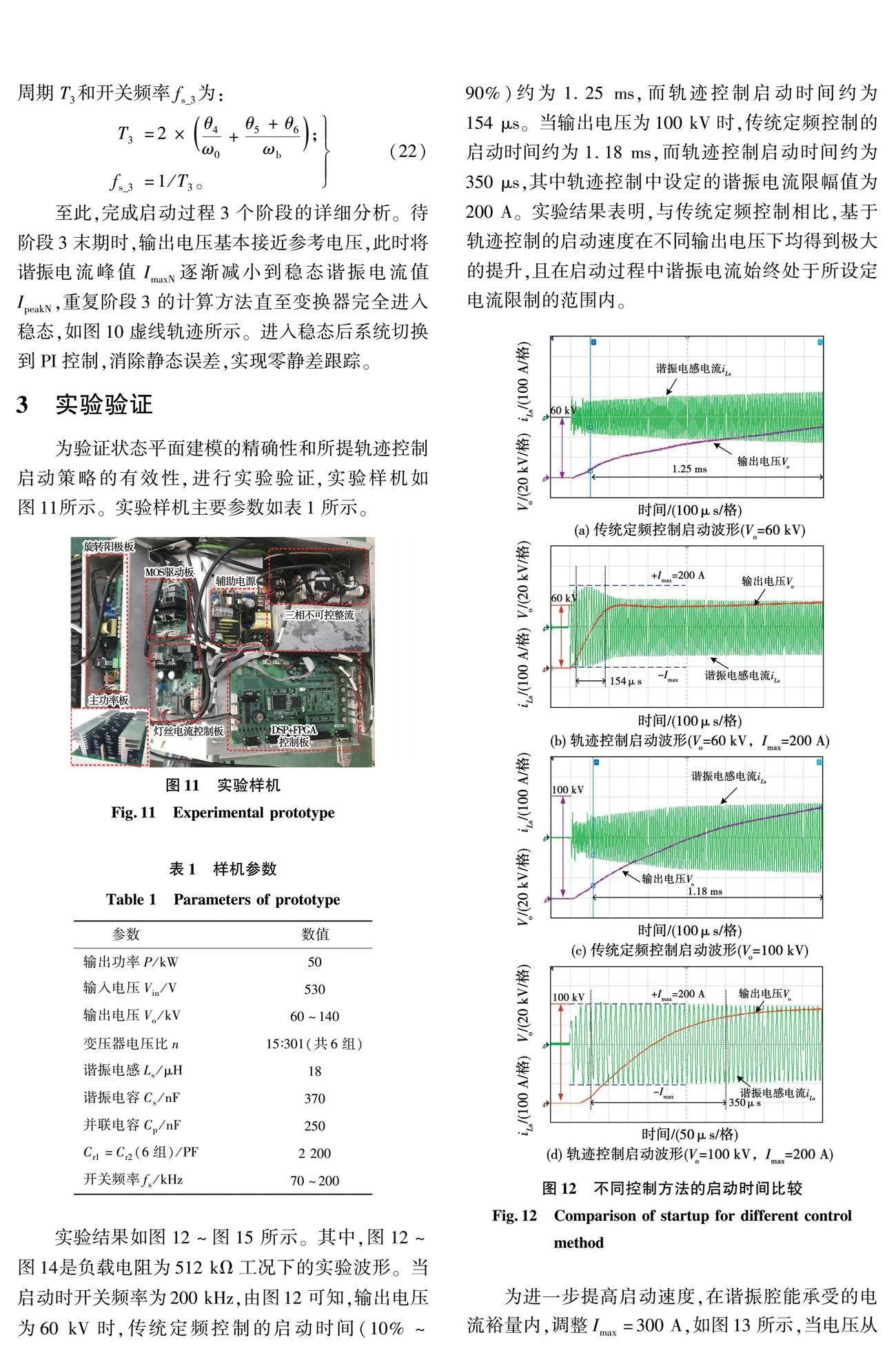
为验证状态平面建模的精确性和所提轨迹控制启动策略的有效性，进行了实验验证，实验样机如图11所示。实验样机主要参数如表1所示。

实验结果如图12～图15所示。其中图12～图14是负载电阻为512kΩ工况下的实验波形。当启动时开关频率为200kHz，由图12可知，输出电压为60kV时，传统定频控制的启动时间（10%～90%）约为1.25ms，而轨迹控制启动时间约为154μs。当输出电压为100kV时，传统定频控制的启动时间约为1.18ms，而轨迹控制启动时间约为350μs，其中轨迹控制中设定的谐振电流限幅值为200A。实验结果表明，与传统定频控制相比，基于轨迹控制的启动速度在不同输出电压下均得到极大的提升，且在启动过程中谐振电流始终处于所设定电流限制的范围内。

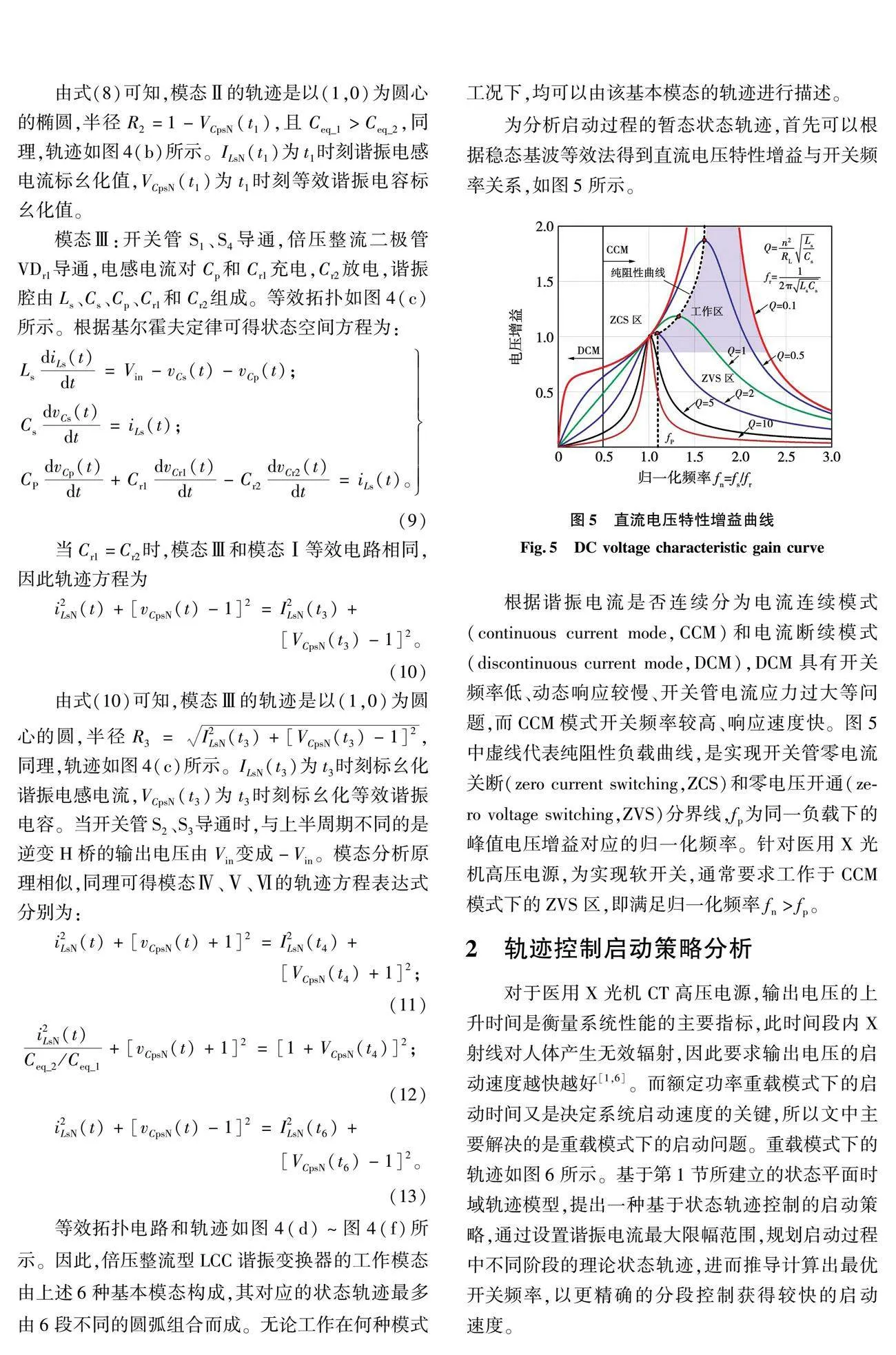
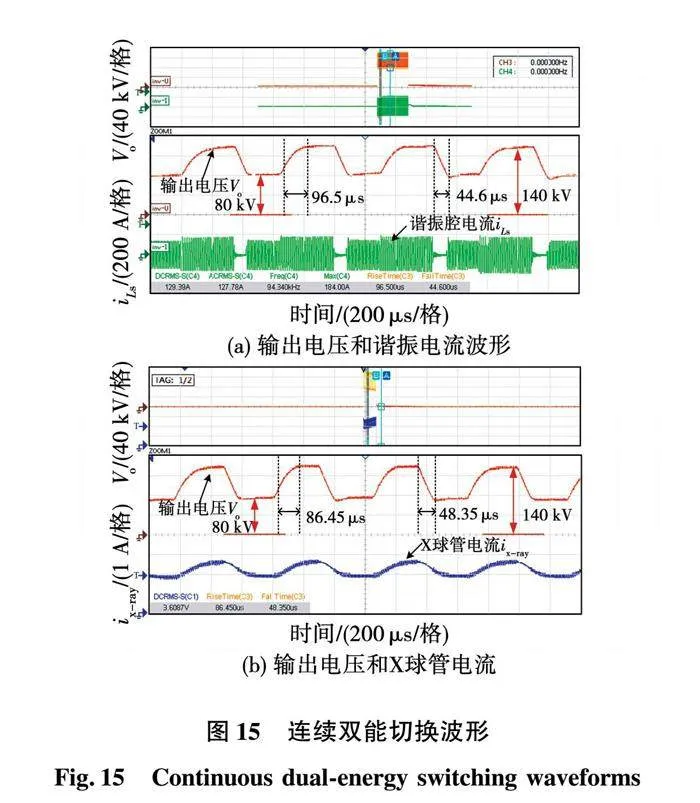
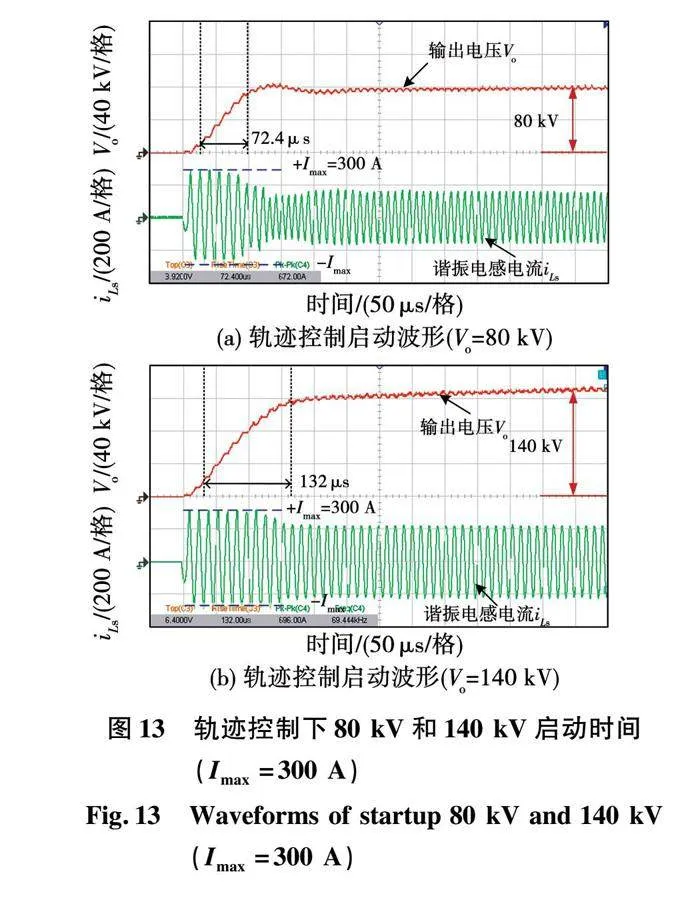
为进一步提高启动速度，在谐振腔能承受的电流裕量内，调整Imax=300A，如图13所示，当电压从0启动到80和140kV时，启动时间分别约为72.4和132μs，启动速度有了明显的提高，可知，Imax值对启动速率有一定影响。当电压在80和140kV之间进行切换时，上升时间约为95.8μs，下降时间约为184μs，均能控制在200μs以内，如图14所示。实验结果验证了所提控制能提高系统的动态响应速度，同时也保证在切换过程中谐振腔不出现电流、电压过冲，实现了快速平滑的切换效果。

图15为当纯负载电阻换成实际的X射线球管后的实验结果，其他工作条件不变，工作模式设置成连续双能切换过程。从实验波形可以看出，当输出电压在80和140kV之间进行连续脉冲式切换时，上升时间可控制在100μs以内，下降时间可控制在50μs以内，同时谐振腔电流和X射线球管电流均无过冲，实现了良好的快速切换效果。进一步验证了所提建模方法和控制策略的优越性。

4 结 "论

针对倍压整流型LCC谐振变换器建模不精确和启动控制效果差的问题，本文提出一种状态轨迹控制策略。首先，基于状态平面分析法，推导出各工作模态的解析模型和轨迹方程，将变换器状态变量的轨迹曲线清晰展现在二维平面内。在状态轨迹模型基础上，提出轨迹控制启动策略，通过设置谐振电流最大限幅范围，来规划启动过程中三个阶段的理论状态轨迹，推导出最优开关频率，使得变换器启动时间加快。最后，通过样机实验验证了所提控制策略的正确性和有效性。实验结果表明，与传统控制方法相比，在保证无谐振电流、电压过冲的情况下，一方面启动速率得到了极大的提升，另一方面也实现了不同电压等级之间的快速切换。

参 考 文 献：

[1] POKRYVAILO A， CARP C， SCAPELLATI C. A 100kW high voltage power supply for dual energy computer tomography applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation， 2015， 22（4）： 1945.

[2] 伍梁， 孙晓玮， 赵钧，等. 基于大信号模型的多模块LCC级联变换器输出电压不均衡分析法[J]. 电工技术学报， 2020， 35（24）： 5142.

WU Liang， SUN Xiaowei， ZHAO Jun， et al. Analysis of output voltage imbalance for cascaded multi-module LCC converters based on large-signal model[J]. Transactions of China Electrotechnical Society， 2020， 35（24）： 5142.

[3] MARTÍN-RAMOS J A， PARDO-VAQUERO Ó， DIAZ J， et al. Modelling a multilevel LCC resonant AC-DC converter for wide variations in the input and the load[J]. IEEE Transactions on Power Electronics， 2019，34（6）： 5217.

[4] PENG Han， CHEN Jimin， CHENG Zhipeng， et al. Accuracy-enhanced miller capacitor modeling and switching performance prediction for efficient SiC design in high-frequency X-ray high-voltage generators[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2020， 8（1）： 179.

[5] LIU Chunhui， ZHANG Zhengda， LIU Yifu， et al. Mega-Hertz high voltage EMAT pulser based on LCC resonant inverter using SiC MOSFETs[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2023， 11（4）：3633.

[6] PERNÍA A M， VAQUERO O P， VILLEGAS P J， et al. LCC resonant multilevel converter for X-ray application[J]. "Energies， 2017， 10（1）： 1573.

[7] 张治国， 谢运祥， 袁兆梅. 一种高频LCC谐振变换器的近似分析方法[J]. 电机与控制学报， 2011， 15（7）： 44.

ZHANG Zhiguo， XIE Yunxiang， YUAN Zhaomei. Novel proximate analysis method of LCC resonant converter for high frequency application[J].Electric Machines and Control， 2011， 15（7）： 44.

[8] LIN Chudi， HE Liqun， LI Xiaohui， et al. Modeling and digital control of 100kV/50kW high voltage power supply based on PPSS-LCC for X-ray generator[C]//IEEE 4th International Electrical Energy Conference， May 28-30， 2021，Wuhan， China. 2021： 1-6.

[9] SEONG-HO S， JUNG-SOO B， TAE-HYUN K，et al. Development of 80kW high voltage power supply for X-ray generator[J]. IEEE Transactions on Industrial Electronics， 2023， 70（4）： 3652.

[10] 周国华，范先焱，许多，等.具有宽范围输入和高效率的改进型LLC谐振变换器[J].电机与控制学报，2020，24（10）：9.

ZHOU Guohua， FAN Xianyan， XU Duo，et al. Improved LLC resonant converter with wide range input and high efficiency[J].Electric Machines and Control， 2020， 24（10）： 9.

[11] POKRYVAILO A. A high-power 200kV power supply for capacitor charging applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation， 2017， 24（4）： 2088.

[12] ZHANG Shanlu， LI Lei， ZHAO Zhennan， et al. Optimal trajectory based start-up control of LCC resonant converter for X-ray generator applications[J]. Energy Reports， 2022， 8（5）： 957.

[13] STEIGERWALD R L. A comparison of half-bridge resonant converter topologies[J]. IEEE Transactions on Power Electronics， 1988， 3（2）： 174.

[14] CHEN Yiming， XU Jianping， SHA Jing， et al. An improved fundamental harmonic approximation to describe filter inductor influence on steady-state performance of parallel-type resonant converter[J]. IEEE Transactions on Power Electronics， 2019， 34（3）： 2467.

[15] IVENSKY G， KATS A， BEN-YAAKOV S. A novel RC model of capacitive-loaded parallel and series-parallel resonant DC-DC converters[C]//Record 28th Annual IEEE Power Electronics Specialists Conference， June 27， 1997， Saint Louis， MO， USA. 1997： 958-964.

[16] 赵子先，康龙云，于玮，等. 基于简化时域模型的CLLC直流变换器参数设计[J].电工技术学报， 2022， 37（5）： 1266.

ZHAO Zixian， KANG Longyun， YU Wei， et al. Parameter design method of CLLC DC-DC converter based on simplified time domain model[J]. Transactions of China Electrotechnical Society， 2022， 37（5）： 1266.

[17] YANG Rui， DING Hongfa， XU Yun， et al. An analytical steady-state model of LCC type series-parallel resonant converter with capacitive output filter[J]. IEEE Transactions on Power Electronics， 2014， 29（1）： 330.

[18] ORUGANTI R， LEE F C. Resonant power pcessors， Part I-state plane analysis[J]. IEEE Transactions on Industry Application， 1985， 21（6）： 1453.

[19] FENG Weiyi， LEE F C. Optimal trajectory control of burst mode for LLC resonant converter[J]. IEEE Transactions on Power Electronics， 2013， 28（1）： 457.

[20] FEI Chao， LEE F C， LI Qiang. Digital implementation of soft start-up and short-circuit protection for high-frequency LLC converters with optimal trajectory control （OTC）[J]. IEEE Transactions on Power Electronics， 2017， 32（10）： 8008.

[21] FEI Chao， LI Qiang， LEE F C. Digital implementation of light-load efficiency improvement for high-frequency LLC converters with simplified optimal trajectory control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2018， 6（4）： 1850.

[22] CHEN Hao， SNG E K K， TSENG K. Optimum trajectory switching control for series-parallel resonant converter[J]. IEEE Transactions on Industrial Electronics， 2006， 53（5）： 1555.

[23] 张治国， 谢运祥， 袁兆梅. 高频LCC谐振变换器的分析与轨迹控制[J]. 中国电机工程学报， 2011， 31（27）： 55.

ZHANG Zhiguo， XIE Yunxiang， YUAN Zhaomei．Analysis and trajectory control of LCC resonant converter for high frequency applications[J]． Proceedings of the CSEE， 2011， 31（27）： 55.

[24] XU Yun， LU Chao， YU Zhiyuan， et al. Multimode constant power control strategy for LCC resonant capacitor charging power supply based on state plane analysis[J]. IEEE Transactions on Power Electronics， 2021， 36（7）： 8399.

[25] ZHANG Hongyin， TONG Channan. Normalized analysis and optimal design of DCM-LCC resonant converter for high-voltage power supply[J]. IEEE Transactions on Industrial Electronics， 2020， 67（6）： 4496.

[26] 张洪寅，童朝南，王泽庭.基于临界模态的DCM-LCC谐振变换器的归一化分析与设计[J].电工技术学报， 2019， 34（1）： 106.

ZHANG Hongyin， TONG Chaonan， WANG Zeting. Normalized analysis and design of DCM-LCC resonant converter based on critical current mode[J]. Transactions of China Electrotechnical Society， 2019， 34（1）：106.

[27] ZHAO Jun， CHEN Guozhu， WU Liang. Fast and accurate control strategy for LCC resonant converters based on simplified state trajectory and two-point solution method[J]. IEEE Transactions on Power Electronics， 2022， 37（5）： 5309.

[28] WU Liang， ZHAO Jun， LIN Hongyi. State trajectory control of startup for LCC resonant converters with capacitive output filter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2021， 9（2）： 2320.

（编辑：邱赫男）