HPM视角下中职教材的编写

摘要：中职数学史的运用存在“高评价、低应用”的境遇，以中职数学教材高教版（第三版）基础模块为例，以HPM视角下“历史发生原理”与“再创造”原理为指导，以中等职业学校课程标准为准则，从HPM的视角出发，对本例教材中数学史的融入情况进行分析探讨，发现当前中职教材中数学史的运用策略、编排形式、史料内容具有单调性；运用水平不足，大部分停留在点缀式和附加式等直接运用水平。基于此，为后续中职数学教材编写提出以下建议：增加隐性史料比重，提升史料运用水平；丰富史料内容，发挥价值引领；加强信息技术利用，科技与教育有机融合；注重“专家+教师”合作，发挥史料高应用效能。

关键词：HPM；数学史与数学教育；中等职业教育；数学教材

中图分类号：G71

文献标志码：A

文章编号：1009-4156（2024）08-0061-07

《教育部关于深化职业教育教学改革全面提高人才培养质量的若干意见》强调，职业教育要落实立德树人根本任务，要发挥人文学科的独特育人优势，注重学生文化素质、科学素养的培养［1］。教材是实施课程标准的主要载体，《中等职业学校数学课程标准》（以下简称《课标》）指出，中职数学教材的编写要遵循规范性、科学性、适用性、人文性、时代性等基本原则。教材编写应突出数学的育人功能，体现数学的思想、知识、方法、观点以及它们的形成和发展过程，通俗易懂，图文并茂，要注意渗透数学文化和批判质疑的科学精神［2］。

HPM是21世纪数学教育的重要研究领域，HPM是数学史与数学教育的简称，全称是History and Pedagogy of Mathematics。HPM研究的主要内容涉及“以数学教育为取向”的价值研究、数学史的教学设计研究、HPM的教学实践、HPM的理论研究等。“以数学教育为取向”的研究是HPM领域的热点话题，在教材中编入数学史不仅可以加深学生对数学概念、方法和思想的理解，激发学习兴趣，还可以让学生体验数学家的创造过程，体会到数学家精益求精的科学精神、求真务实的品德，对于激发学生们的民族自豪感以及民族自信心都有明显的效果［3］。

HPM架起了科学和人文的桥梁，在当前的中职教材各个版本中，对于数学思想、知识、方法以及形成的过程等数学文化渗透明显不足。数学书本上的知识，经过编者们反复推敲，变得十分系统严谨，充满数理逻辑，但缺乏人文体验，使得中职学生产生数学难以理解、枯燥乏味、学无以用等印象，然而HPM研究的深入为数学课程带来了崭新的体验。如何将数学史与数学知识有机融合，更好地发挥其德育价值和教学效果是教材编写的一个难题。以中职数学教材高教版（第三版）基础模块为例，分析教材数学史运用情况，在科技发展的当前社会，提出一些反思和建议，为后面教材编写提供一些帮助。

一、HPM视角下编写教材的理论依据

《课标》要求突出数学的育人功能，将数学中的思想、知识、方法以及形成过程和发展过程体现出来，将数学史与数学教育有机结合，注重数学教材编写的历史发生原理和“再创造”原理，将数学史隐性融入教材中，可以达到“润物细无声”的效果。

（一）历史发生原理

1.理论的产生

历史发生原理是HPM视角下教材编写的理论依据之一，历史发生原理兴起于19世纪，源自德国生物学家赫尔克提出的生物发生律，个体发生是种系发生短暂而迅速的重演，是由遗传和适应的生理作用决定的［4］。后来，此原理被迁移到教育学中，即“个体知识的发生过程遵循人类知识的发生过程”。英国教育家斯宾塞是这个理论的支持者，他简明扼要地指出，“儿童的教育，无论在方式上，或在安排上，均须与历史上人类的教育相对应。换言之，个人知识的发生必须遵循种族知识发生的途径”［5］。数学家们也认为这条原理在数学界同样适用，荷兰著名数学家和数学教育家弗赖登塔尔指出：“数学史是一个图式化不断演进的系统化的学习过程，儿童无须重蹈人类的历史，但他们也不可能从前人止步的地方开始。从某种意义上说，儿童应该重蹈历史，尽管不是实际发生的历史，而是倘若我们的祖先已经知道我们今天有幸知道的东西，将会发生的历史。”［6］法国数学家庞加莱指出：“教育工作者的任务就是让儿童的思维经历其祖先之所经历，迅速通过某些阶段而不跳过任何阶段，鉴于此，科学史应该是我们的指南。”［7］历史发生原理受到数学家们的推崇，他们认为学生对数学知识的学习理解、思考都和历史上的数学家有相似的境遇。

2.实证的检验

20世纪末以来，越来越多的国际学者参与到实践的检验中，在国外，Paola将历史上著名的“点数问题”用于概率的教学，发现了学生的解法与历史上数学家的解法具有相似性［7］。华东师范大学的殷克明通过高中生对切线的理解进行研究，实验表明绝大多数高中生对切线的理解只达到古典几何阶段，即他们只是根据公共点个数、直线与曲线相对位置或直线与圆半径位置关系来判别切线，与古希腊欧几里得、阿波罗尼斯、阿基米德等人的理解具有相似性。绝大多数高中生未能从特殊曲线圆和圆锥曲线的切线顺利过渡到一般曲线的切线，在历史上，切线的概念也经历了漫长的过程，这也表现出高度的历史相似性［8］。国内外诸多学者的研究均表明学生学习数学的心理机制规律与数学发展历史存在相似性。

发生教学法是历史发生原理应用于教学实践的体现，通过研读历史可以从中获取特定主题的知识的来源及发展，再经过加工处理，走进教材，基于历史进行适当的教学设计，结合课程标准和学生实际学情，组织特定主题的教学策略和表征知识进行课堂教学［4］。将数学史融入教材可以按照以下四个步骤进行：一是了解所授主题内容的历史；二是理解主题历史的关键步骤和思想方法；三是重构问题和过程；四是采用问题驱动模式进行教学。

（二）“再创造”原理

1.原理的含义

“再创造”原理也是HPM视角下教材编写的理论依据之一，它是荷兰数学家和数学教育家弗赖登塔尔提出的，“再创造”就是学生本人将要学习的内容自己去发现或者创造出来。弗赖登塔尔认为，“学一个活动最好的方式就是做”，只有这样，才能把获得的知识得到最深的理解和最长久的保持［9］。现在的数学教学直接将结果呈现给学生，把结果作为出发点，将思维过程颠倒，得出结论后再带学生进行公式定理的练习、运用。弗赖登塔尔认为，这种数学学习方式是“教学法的颠倒”，他指出：“这种方法是对创造思维过程的掩藏。”［9］这种方式不仅不会使学生真正地掌握数学，反而会使学生觉得数学是枯燥、刻板的逻辑定理。真正的数学应该展示数学家们发明和创造的过程，包含所经历的挫折、错误以及不同时代的思考等，这就是他所提倡的活动或者创新的数学。弗赖登塔尔对其“再创造”理论中的思想进行层次划分［10］（见表1）。

2.实践的运用

有学者将数学史融入教材的分类标准划分为五类，即点缀式、附加式、复制式、顺应式、重构式［11］。“再创造”思想运用于数学教材中最直接的体现是顺应式和重构式这两种方式。顺应式和重构式都是根据教学设计安排将数学史料进行改编、重构，以润物细无声的方式融入各个教学环节，按数学知识发生发展的顺序展现相关的数学知识，让学生在无意中经历数学的“再创造”过程［12］。数学史融入教材的呈现形式可分为显性和隐性。显性呈现是指数学知识以直接表征的形式呈现出来，如数学家画像、数学家介绍、数学概念的起源简介、数学符号的历史渊源以及数学历史经典名题等，常用的方式是点缀式、附加式、复制式。隐性呈现是指根据教学内容搜集相关史料，进行筛选、改编、重构，将历史隐藏在教学的各个环节，贯穿始终，顺应式和重构式属于隐性呈现的形式，根据表2分类描述，顺应式和重构式都属于“再创造”思想的体现，属于高水平的运用形式。

二、当前中职教材的数学史

（一）当前中职教材数学史的运用形式

根据表2的分类方式，对中职数学教材高教版（第三版）基础模块中的数学史料运用形式进行分析。基础模块分为上、下两册。基础模块上册内容包括集合与充要条件、不等式、函数、指数函数与对数函数、三角函数。书后附有“预备知识”。基础模块下册内容包括数列、平面向量、直线与圆的方程、立体几何、概率与统计初步。共有十个章节。

1.点缀式

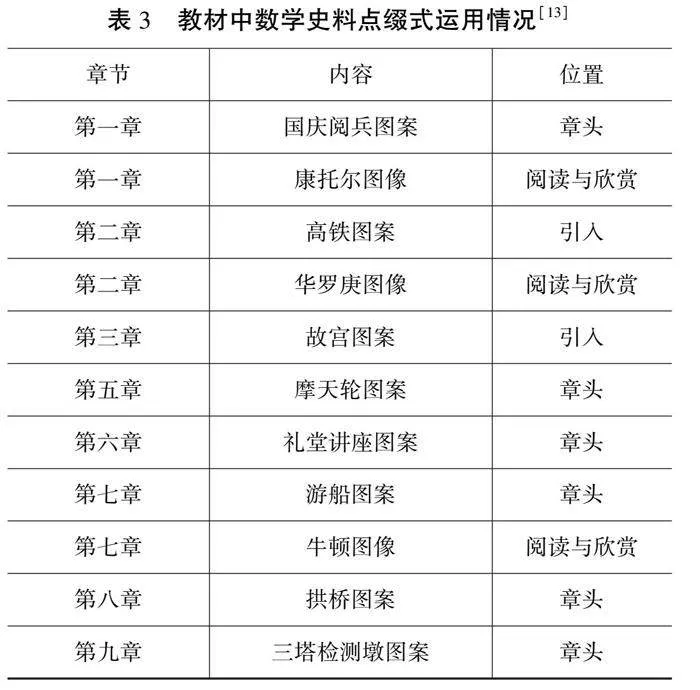
点缀式的出现一般在各个章节的章头和章末部分，包括一些数学家的肖像或与教学有关的数学图案等。当前教材运用点缀式最多的地方是章头、引入、阅读与欣赏部分。在章头和引入部分的图案一般是与本章节所授主题息息相关的，用来引出所讲授的内容，引起学生注意力或是引发学生思考讨论进入教学程序。在阅读与欣赏部分都是呈现数学家的图像，使学生对于文字阅读的信息有更加具象的理解。例如，在学完第八章直线与圆后，介绍卡迪尔这位将代数与几何统一起来的伟大数学家，是对正文学习内容的补充，看着数学家的图像，可以更具体地感受到数学家的睿智、严谨、沉稳的风格形象。再如，第九章平静的湖面用于引入新知识“平面”的概念，与学生生活相关，在学生已有的认知上学习新的知识，遵循了教育规律。点缀式运用情况统计见表3。

2.附加式

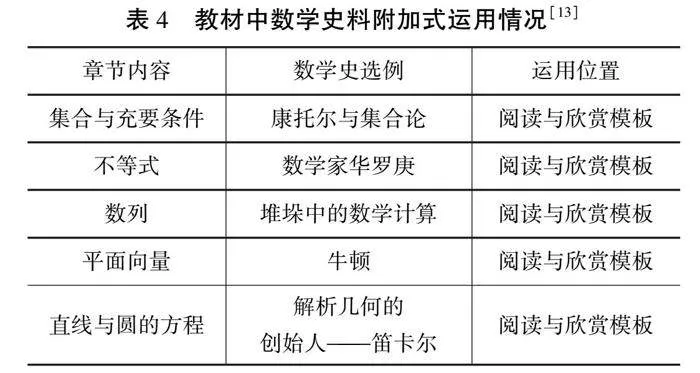
附加式是指有关数学史的文字阅读资料，当前教材附加式的运用主要出现在各章节的末尾“阅读与欣赏部分”，主要分为两类，即数学家生平和主要成果的介绍、历史中数学思想。附加式的运用一般是独立于教材融入，主要是为了提供拓展阅读，激发学习兴趣，培养学生对数学的积极情感态度。表4给出了部分附加式的数学史例子。

3.其他运用形式

复制式一般是出现在例题中，通过历史上的数学问题、名题解法进行教学，在教材中出现得较少。在数学（下）“等差数列求和”这一小节中，介绍求和公式就运用了数学王子“高斯”的解题方法，高斯在上小学的时候，数学老师在数学课上出了一道题目“把1到100的整数写下来，并把他们都加起来”这个题目对于10岁的小朋友来说是很难的，对于高中生而言，可能有一定的生活实践经验，会想到首尾相加的方法，也是符合学生认知水平的一道题目。通过首尾相加的方法，可以很快得出答案，将这个数学思想一般化形成数学公式，就可以得到等差数列求和的第一种公式，即Sn=（a1+an）n2。

顺应式一般出现在例题、习题中，通过对历史名题进行改编，使之符合当前课堂情景和学生水平。数学（下）在“等差数列的求和”的练习题中有一道题就是根据“堆垛中的数学”进行改编，练习题第一题：“堆放钢管的V形架的最下面一层放一根钢管，往上每一层都比它下面一层多放一根，最上面一层放30根钢管，问这个V形架上共放着多少根钢管？”［13］此问题将实际情景和数学知识紧密联系，需要学生将所学内容灵活应用，从题目中得到信息：首项为1，第n项为30，公差为1，求项数。根据公式an=a1+（n-1）d，带入即可求解。在“堆垛中的数学”中，也是讨论类似的问题，在本章节的阅读与欣赏部分提供了与“堆垛中的数学”的相关阅读和思考：“长方垛的每一层都是长方形，长方形上的每一层长边比短边堆放的物体都多一个，共有n层，从上往下数，最上面的一层放了2个，第二层放了6个，第三层放了12个，等等，以此类推，求它的通项公式。”［13］关于堆垛术的题目，我国古代的沈括、杨辉、李善兰等数学家都曾研究过。

重构式一般隐藏于所授主题的各个环节，在整个教学脉络中贯穿始终。对教材的编写和教师的教学水平都有极高的要求，是“为教育而历史”的高层次水平运用。在本版教材中，并未有重构式的运用形式。

（二）当前中职教材数学史的运用现状分析

1.使用策略、编排形式、史料内容的单调性

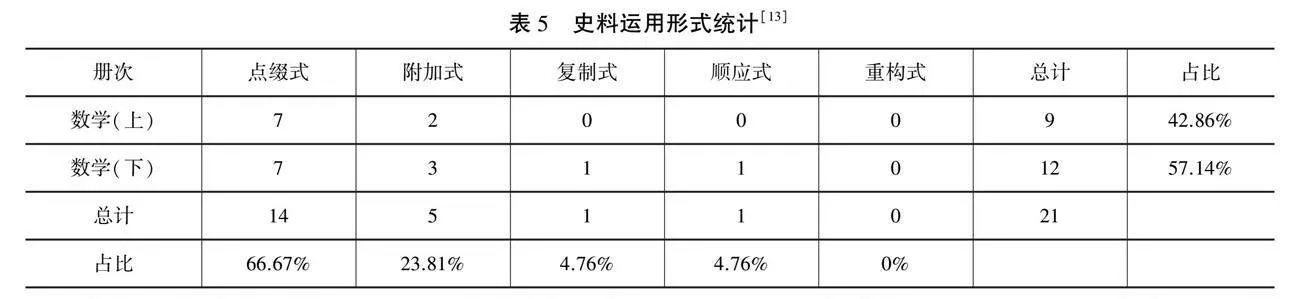
首先，教材中使用策略呈现单一性。在教材中主要运用的是点缀式和附加式，出现在章节、章头和章末的“阅读与欣赏”位置。点缀式的运用在上册和下册比较平均，运用的次数均为7处，占比达到66.67%；附加式的运用虽然比较均匀，但是次数较少，上册2次、下册3次，占比达到23.81%。顺应式和复制式在上册中没有出现，在下册中也只出现过一次占比均是4.76%。重构式未出现。可以得出本教材数学史运用层次也大多停留在点缀式或附加式等直接运用的方式。属于“为历史而历史”的阶段，将教材上册和下册中运用史料进行统计（见表5）。

其次，编排形式的单调性。本版教材的栏目设置分别是章头、引入、知识点总结、例题、练习、旁白、复习题、拓展阅读等8个栏目。本教材中数学史的位置主要设置在非正文部分，在每章节结尾进行拓展阅读，将本书中的数学史使用位置进行统计，得出在章头的运用占比41%，其次是阅读与欣赏部分，占比29%，引入部分占比18%，然而正文中的运用不足30%，习题部分和例题部分涉及极少，各占6%，可以得出正文栏目与数学史极少产生联系，分布的位置不均匀、不广泛，仅靠章头的图案引入和课后的拓展阅读达到数学史的育人目的，是远远不够的。

最后，素材内容的单调性。本教材总共有10个章节，却仅有5篇数学史料阅读。其中，关于数学家的介绍有3篇，历史名题只有1篇，内容概念史只有1篇。选取的内容不够丰富，相对于普通高中知识点的减少和知识难度的降低，这些课外阅读明显不够。本教材中选取的数学史料主要分为以下三种类型：第一种是数学家的介绍，分别介绍了条件艰苦仍刻苦钻研数学的华罗庚，充满好奇心、喜欢思考的牛顿，提倡理性、主张科学的笛卡尔；第二种是内容概念史，介绍了康托尔和集合论，康托尔针对无穷集合提出了集合论，史料的呈现拓展了学生学习集合的认知；第三种是历史名题，介绍了堆垛中的数学，生活中常见的现象也蕴含数列的知识。有关数学符号的由来、历史典故、经典的图形等没有涉及，数学史涵盖的爱国精神、创新精神、求实精神、奉献精神、协同精神和育人精神等并没有得到明显呈现。本教材选取的数学史数量较少，内容不够丰富。

2.运用水平浅层次

整套教材对数学史料的运用水平可以根据计算公式进行量化，首先按数学史的运用层次赋值，即点缀式赋值为 1，附加式赋值为2，复制式赋值为3，顺应式赋值为4，重构式赋值为5，再利用如下公式计算教材中数学史的运用水平：L=∑AiBin（i=1，2，3，4，5），其中，Ai表示所处水平的数学史的数量，Bi表示数学史所处水平的赋值，即Bi=i，n表示教材中数学史的总数［12］。通过表5，可得附加式、复制式、顺应式、重构式的运用次数分别是14、5、1、1、0。经过计算，可以得到史料的运用水平为L=14×1+5×2+1×3+1×4+0×521=1.46。与普通高中人教A 、B两版教材的运用水平进行比较，人教版A教材5册教材的运用水平L=2.29，人教版B教材5册教材的运用水平L=2.78［14］。可以得出，当前教材的数学史运用水平较低，主要停留在史料的直接表征层次，以显性呈现的方式为主。数学史料未融入主要的学习环节中，并没有发挥真正的育人价值，无法让学生经历“再创造”的过程，难以发现数学史料蕴藏的数学思想，内容浅尝辄止并且大多位置编排在章头和章末，与正文内容脱节，会让学生产生可学可不学的心理，出现数学史“高评价、低应用”的局面。

三、教材编写的建议

（一）增加隐性史料比重，提升史料运用水平

数学史融入教材的呈现形式可分为显性和隐性。显性是指数学知识以直接表征的形式呈现出来，隐性呈现是指将历史隐藏在教学的各个环节，在学生学习的过程中经历“再创造过程”达到润物细无声的效果。《课标》指出，教材编写应突出数学的育人功能，体现数学的思想、知识、方法、观点以及它们的形成和发展过程［2］。中职数学学科有很大一个特点，即“重练习，轻理解”，教材设计环节大多是引入问题、例题讲解、公式或定理给出、练习等环节，围绕知识点设计问题，注重对公式或定理的运用练习，但是缺乏认同体验。

教材的编写应增加隐性史料比重，史料运用顺应式和重构式的形式融入教材，提升史料运用水平，有助于产生学习动机，激发学习兴趣。历史发生原理表明：历史发生的过程遵循人类知识发生的过程，学生数学学习的过程也往往和历史上数学家的境遇相似，以重构式的方式设计教学，主张学生体验历史的演变，将知识点融入问题产生的背景、难点中，设计关键环节展示数学家的解题思想。以三角函数为例，学生在学习的过程中需要学习到与前期学习阶段不同的概念、需要熟练运用大量的变换公式、理解函数这个抽象概念本身的难度等，学生在真正的学习过程中往往出现“公式记得牢，做题理解差”的情况。李长龙在自己的硕士毕业论文中研究“三角函数”章节的教学问题，通过对学生的情况分析，通过比较基于历史发生原理的教学方式与基于教材的设计方式得出前者更能有效解决学生学习困难，提高学生学习的兴趣，促进对知识的掌握和理解，教师也更倾向于历史发生原理融入数学课堂［15］。汪晓勤等人基于“历史发生原理”设计“椭圆”课程的教学，并对723名学生进行研究，得出课程的设计深深吸引学生，绝大多数学生能理解和掌握椭圆焦半径性质的推导过程，在课程的设计中做到“借鉴历史，重演历史，理解历史”［6］。

（二）丰富史料内容，发挥价值引领

针对中职学生的实际学情，教材的编写更要重视可读性、趣味性以及与实际生活相关性。数学史材料选择的依据要有一定的思想性，突出数学思想或方法的发展，突出数学家追求真理、刻苦钻研的精神［16］。数学史材料的选择应当注重实施效果和教学目的。史料的选择类型一般含有趣闻轶事、数学发展历史、符号历史、经典名题、美育培养、爱国教育、创新精神、求实精神、奉献精神、协同精神等。以爱国精神为例，作为具有五千多年文明史的文化大国，我国历史上的数学成就灿烂辉煌，秦九韶撰写的《数书九章》中，“大衍求一术”使一次同余式组的解法规格化，比高斯创用的同类方法早500多年，正负开方术比19世纪英国霍纳的同类方法早500多年。刘徽的“割圆术”、出入相补原理，祖冲之关于圆周率的计算，刘徽、祖暅关于球体积的研究，李善兰恒等式，“整体微分几何之父”陈省身，著名数学家陈景润、熊庆来、华罗庚等为我国的数学事业作出了非凡贡献。中国古代数学是四大人类文明的组成部分，虽然总体上发展比较晚，但是有其自身的优势，有其独立的体系和独创的辉煌［17］。

融入数学史是为了更好地发挥其兴趣引领、德育教育、思维创新等教学目的，所以在内容的选取上重视有趣的数学图片、历史名题，在选取古代数学名题时要注意给予适当的备注，不然太过晦涩也会使学生丧失阅读的兴趣。在选取中国古代的数学思想、现代的数学成就时要注意结合今天的历史发展，贴合当下的社会价值观，达到育人的目的。选取数学符号由来、数学发展史、数学方法的创立等要与章节内容呼应，使学生更好地理解数学内容。选取数学家的科学精神、创新启示等也要注重趣味性和文化性的编写，不要太过学术化。注重数学家中突出贡献的女性形象，增加教材的多元化，让学生更好地了解数学、认识数学，从而学好数学。

（三）加强信息技术利用，科技与教育有机融合

《课标》指出：“教材的编写要注重时代性，应具有先进的教学理念，能够反映时代特性，体现时代发展趋势。教材要充分利用现代教育手段，为师生提供文字、图像、音频、视频等丰富生动的教学资源。”［2］教材应积极开发中职教育课程的数字文化资源，使教育科技化。在“互联网+教育”的时代，教育的形式也发生了巨大的变化。信息技术具有直观性、趣味性、生动性的特点，信息技术可以使学生直观动态地捕捉函数运动的过程、数学公式换算过程等，在以前只能自我构想的立体图形，通过数形结合的场景完美地展现在学生眼前；同理，数学史的发展历程亦可通过信息技术的完善而进一步落实到万千课堂， 线上线下融合式的课例研究成为主流。

在课例教学中，教师可结合几何画板、GeoGebra、希沃白板、流转笔记等信息化工具，再现数学家探寻概念公式、命题定理等过程; 借助HPM 微视频，生动地展示数学知识的来龙去脉、数学思想的古今传承，彰显不同时期、不同国家数学文化的历史性、人文性［18］。以“椭圆”的教学为例，常规的教学方式是用一支笔、一根固定长的绳子还有两个固定的点画出椭圆，引出定义，推导方程，但很明显，学生对于为什么要学习椭圆、椭圆的历史、学习椭圆的意义等均未了解，缺乏学习动机。有学者以历史发生原理为基础，以信息技术为工具，设计本章节的教学活动，通过动画演示椭圆产生过程，符合学生认知，直观形象地再现椭圆轨迹的画法，提升学生的空间思维能力［19］。在上课之前，学生可以通过微课二维码的视频了解到本章节涉及的数学大家、历史典故、内容发展等相关内容，不仅可以吸引学生注意力，而且还可以加深数学思想和方法的理解。改变对数学的刻板印象，数学不再是古板、乏味的代名词，而是充满探索、充满未知、充满人文的艺术殿堂。

（四）注重“专家+教师”合作，发挥史料高应用效能

在教材的编写中要着重关注到数学史专家的力量与一线教师的教学实践，专家可以为教材的编写提供详尽可靠的数学史料，确保教材编写的科学性和系统性，教师可以反馈史料的实施效果，当前，“专家+教师”的协同模式对中职教材的编写具有借鉴意义。当前数学史的教育价值已受到国际学者的认可，我国的HPM研究也注重教学实践，但是数学史存在的“高评价，低应用”的现象仍屡见不鲜，主要存在四个方面的原因：一是一线教师认识的缺位；二是教材中数学史素材还相对缺乏；三是数学史素材呈现方式的单一；四是教材之外适用的教学资料缺乏［20］。数学史的教育价值在数学教育家看来不必赘述，但是在一线教师中可能知之甚少。一方面，教师忙于日常教学事务，对前端学术疏于了解；另一方面，教师缺乏对数学史的重视，可能会将史料素材弃之不理，或者只做课后阅读。数学史料的素材提供得较少，不能使教师融会贯通地进行教学，缺乏课程资源。即使有教师清楚数学史的教育价值，也难以有充足的时间从史料库中找寻自己的教学素材。

专家和教师在合作编写教材时应考虑到数学史的选取原则，教师与专家的合作可以避免数学史料的运用水平停留在浅层次阶段，以重构式或顺应式的方式进行教材编写。专家和教师的合作模式可以借鉴PDCA循环理论的实施形式：P——PLAN，这一环节主要是指明确目标，制定措施；D——DO，这一环节是指执行目标，实施计划；C——CHECK，这一环节是指检查结果，查找问题；A——ACTION，这一环节是指采取措施，持续改进。此循环是一个闭环管理系统，不断循环滚动，不断解决问题，提升质量。“专家+教师”合作编写教材的流程为确定章节主题（以此为中心）、专家团队筛选史料、“专家+教师”合作编写教材、教师一线实践、课例反馈，此为一个循环。专家团队和一线教师根据课例反馈重新筛选史料，进入循环，以此往复，不断改进问题，提升教学质量， 达到数学史“高评价、高应用”。

参考文献：

［1］教育部关于深化职业教育教学改革全面提高人才培养质量的若干意见［J］.中华人民共和国国务院公报，2015（34）：48-52.

［2］中华人民共和国教育部制定.中等职业学校数学课程标准（2020年版）［Ｍ］．北京：高等教育出版社，2020：31-33.

［3］杨光，李琳.浅析数学史在教学中的教育价值［J］.内蒙古师范大学学报（教育科学版），2014（12）：12-13.

［4］徐章韬，汪晓勤，梅全雄.认知的历史发生原理及其教学工程化——以数学学科为例［J］.数学教育学报，2012（1）：26-29+42.

［5］斯宾塞.斯宾塞教育论著选［M］.胡毅，王承绪，译.北京：人民教育出版社，2005：95.

［6］汪晓勤，王苗，邹佳晨.HPM视角下的数学教学设计：以椭圆为例［J］.数学教育学报，2011（5）：20-23.

［7］汪晓勤.HPM的若干研究与展望［J］.中学数学月刊，2012（2）：1-5.

［8］殷克明. 高中生对切线的理解：历史相似性研究［D］.上海：华东师范大学，2011.

［9］弗赖登塔尔.作为教育任务的数学［M］.陈昌平，唐瑞芬，译.上海：上海教育出版社，1995：160.

［10］蒲淑萍，汪晓勤.弗赖登塔尔的HPM思想及其教学启示［J］.数学教育学报，2011（6）：20-24.

［11］蒲淑萍，汪晓勤.数学史怎样融入数学教材：以中、法初中数学教材为例［J］.课程·教材·教法，2012（8）：63-68.

［12］覃淋.台湾初中数学教材中的数学史［J］.中学数学杂志，2017（8）：33-37.

［13］李广全.数学教材《基础模块》［M］.北京：高等教育出版社，2018：23-24.

［14］覃淋.我国高中数学教材中数学史的分析与思考［J］.教育导刊，2020（2）：71-79.

［15］李长龙. 基于“历史发生原理”的三角函数教学研究［D］.乌鲁木齐：新疆师范大学，2015.

［16］王青建，陈洪鹏.《数学课程标准》中的数学史及数学文化［J］.大连教育学院学报，2009（4）：40-42.

［17］张奠宙.数学文化课程总体设计需要重视的几个问题［J］.中小学课堂教学研究，2019（2）：6-10.

［18］余庆纯，汪晓勤.基于数学史的数学文化课例研究［J］.中小学课堂教学研究，2021（1）：5-9.

［19］鲁秋野. 信息技术环境下数学史融入教学设计的研究［D］.南昌：江西师范大学，2014.

［20］张生春.数学史与数学课程融合的现状分析［J］.数学通报，2008（5）：15-17+21.

Compilation of Secondary Vocational

Teaching Materials from the Perspective of HPM

Wang Zhonghua Yu Chunhua

（Institute of Education， Guizhou Normal University， Guiyang 550025， China）

Abstract：The application of the history of mathematics in secondary vocational schools is characterized by “high evaluation and low application”. Taking the basic module of secondary vocational mathematics textbook of higher education edition （third edition） as an example， guided by the principle of “historical occurrence” and “re-creation” principle under the perspective of HPM，taking the curriculum standard of secondary vocational schools as the criterion， and from the perspective of HPM， this paper analyzes the integration of the history of mathematics in this example textbook. It is found that the application strategy， arrangement form and historical data content of the history of mathematics in the current secondary vocational textbooks are monotonous. The application level is insufficient， and most of them stay in the direct application level such as embellishment and addition. Based on this， the following suggestions are put forward for the subsequent compilation of secondary vocational mathematics textbooks： increasing the proportion of hidden historical materials， improving the level of use of historical materials; enriching the content of historical materials， giving play to the value of guidance; strengthening the use of information technology， science， organically integrating technology and education; emphasizing the cooperation between experts and teachers， and exerting the high efficiency of historical materials application.

Key words：HPM; History of mathematics and mathematics education; Secondary vocational education; Mathematics textbook