合理设计开放题 提升教学有效性
2024-06-21崔雅
崔雅
摘要:培养学生终身学习能力和数学素养是数学教学的出发点和落脚点.在初中数学教学中,教师可以合理设计开放题,充分发挥开放题的灵活性、创新性、发散性等优势,为学生提供广阔的自由探索空间,以此点燃学生学习热情,激活学生数学思维,提高学生应用数学的能力,培养学生创新意识,促进学生数学核心素养的落实.
关键词:学习能力;数学素养;开放题
当下,在“双新”背景下,初中数学课堂教学越来越关注学生的主体价值,以生为主的学习方式越来越多地被应用于课堂教学中.开放题为学生提供了更广阔的探究空间,其在发散学生数学思维、培养学生创造力、提高学生参与度等方面发挥着重要作用,因而越来越多地得到了一线教师的青睐.开放题的类型多样,答案不唯一,具有较强的灵活性,可以很好地考查学生基础知识和基本技能的掌握情况,可以最大限度地激发学生潜能,锻炼学生的发散思维,提高学生多角度分析和解决问题的能力.不过在课堂教学中,部分教师认为开放题过于灵活、发散,在课堂上探究可能会出现很多“意外”,而这些“意外”会影响教学进度,为此在课堂教学中还是习惯选择那些指向明确的保守题.有时教师即使给出一些开放题,也会给出许多限定条件,指导学生按照预设的思路思考,这样难以发挥开放题的优势,影响学生创新意识的培养.笔者结合教学经验谈谈开放题应用于数学课堂的一些认识,以期引起同行对开放题的重视.
1 巧用开放题,激活思维
无论是在日常练习中,还是在平时考试时,为了便于评价,教师在设计题目时大多追求答案的唯一性,这在一定程度上制约了学生思维的创造性,影响学生创新能力的提升.基于此,在日常教学中,教师不妨结合教学实际设计一些开放题,给学生提供一些遐想的空间,为新知学习制造一些悬念,进而让学生的思维活起来,让课堂动起来.
例如,教学“解二元一次方程”时,在导入环节,教师设计了一个题目:求方程2a+b=18的正整数解.显然该题答案不唯一,由此引发认知冲突,成功地激发了学生探究新知的欲望,让学生的思维活跃起来.
为了帮助学生找到解决问题的方法,教师设计了这样一个游戏活动:教师拿出课前准备的18枚一元硬币,然后选择3名学生参加这个游戏,前两名学生各拿一枚硬币,第三名学生拿走剩余的硬币,然后引导学生用数学语言加以描述,于是得到当a=1,b=16时,2a+b=18,由此得到了一组解.接下来,游戏继续,这次前两名学生各拿2枚硬币,这样第三名学生可以拿到剩余的14枚硬币,于是得到“a=2,b=14”一组解.以此类推,借助游戏学生完成了方程的解答.因为该二元一次方程的答案不唯一,于是代入法求解应运而生.这样通过开放题的解决,学生快速进入学习状态,为新知的学习创造了良好的学习氛围.
课堂导入的方法多种多样,开放题就是其中的一种.恰当的开放题,能够让学生感知原有的方法和思路将难以解决现有的问题,以此激发学生学习动机,让学生快速进入学习状态,使得学生的学变得更加主动、积极,有效提升课堂教学有效性.
2 巧用开放题,发展能力
在数学学习过程中,将知识内化为能力需要一个长期的过程,它不是靠教授来达成的,而是需要学生自己去体验、感悟.在实际教学中,教师应为学生提供一个自由探索的平台,鼓励学生在思考、交流、探索中主动发现、提出并解决问题,让学生学会学习,培养学生终身学习能力.开放题因其题设、条件、方法、答案具有不确定性和不唯一性,可以为学生提供广阔的探究空间,有利于学生自主探究能力的提升,有利于学生终身学习能力的发展.在解答这些开放题时,需要多角度、多层次发散性地去解决问题,这样通过问题的解决既可以培养思维的批判性、灵活性、广阔性,又能提高数学综合应用能力,使得学生思考与分析能力都能得到很好的发展与提升.
例如,学习了菱形相关知识后,教师根据基本学情设计了如下一道开放题:
现有一张长为12 cm、宽为5 cm的长方形卡纸,若在这张卡纸上裁剪出一个菱形,可以怎么裁?菱形的面积是多大?
题目给出后,教师鼓励学生动手画、动手折,通过动手实践进一步感悟菱形的定义及相关性质.从题设信息不难看出,菱形的个数不唯一,这为学生提供了自由探索的空间.
学生经过独立探索,给出了多种不同的解决策略:有的学生用尺子量,尝试剪出一个菱形;有的学生通过折叠分别得到长方形四边的中点,然后将四个中点依次相连,得到了一个菱形;有的学生根据正方形是特殊的菱形这一特点,在长边上截取5 cm,得到了一个菱形……学生通过动手操作得到不同大小、不同形状的菱形后,教师预留充足的时间让学生动手计算,得到菱形的面积.
最后,教师对学生的解答过程进行归纳总结,即解答此类问题最重要的是先画图,然后运用数形结合的思想方法解决问题.这样通过开放题的设计,引导学生从不同角度思考问题,得到了多种解决方案,促进了基础知识的巩固和解题能力的提升.
数学知识是丰富多彩的,解决问题的方法也是多种多样的,在解决同一问题时,思考的角度不同,应用的知识不同,解决方案也会有所不同.教学中切勿用“标准答案”来禁锢学生的思维,应尝试通过开放题为学生创设自由探索的空间,并鼓励学生进行互动交流,以此帮助学生积累基本活动经验,促进学生综合素养的提升.
3 巧用开放题,巩固知识
课堂练习在数学教学中是必不可少的,它是巩固知识、强化技能的重要途径.学生课后时间更加自由,是培养学生个性化思维的最佳时机,因此在课后练习中,教师要根据教学目标和教学内容创设一些有价值的开放性问题,使课后练习的形式更加丰富化,有效锻炼学生的数学思维,加速知识体系建构,培养学生应用数学知识的能力.
例如,在因式分解课后练习中,教师设计了如下一道题:
如果二次三项式x2+ax+12在整数范围内能够分解因式,那么a可以取何值?
题目给出后,教师让学生以小组为单位展开讨论.从学生反馈来看,大多数学生都能想到从常数项入手,即将12进行拆分.教师点名让学生板书答案,学生提出可以将12拆分成3×4,2×6,1×12.该学生话音刚落,其他小组的学生就提出了异议,这里的整数还可以是负整数,还可以将12拆分成(-3)×(-4),(-2)×(-6),(-1)×(-12).这样通过展示与交流,学生得到了完整的解答过程,得到了不同的a值.
该题看似不难,不过与简单的因式分解相比,其难度所有增加,不仅可以考查学生的数学应用能力,而且可以考查学生思维的灵活性、严谨性.从解题反馈情况来看,学生在解答该题时容易漏掉负数的情况,而通过有效的互动交流,学生相互启发、相互补充,充分体会合作学习的价值,培养了合作意识.另外,学生通过开放题的解决,既巩固了因式分解的有关知识,又感受到了数学学习的乐趣.
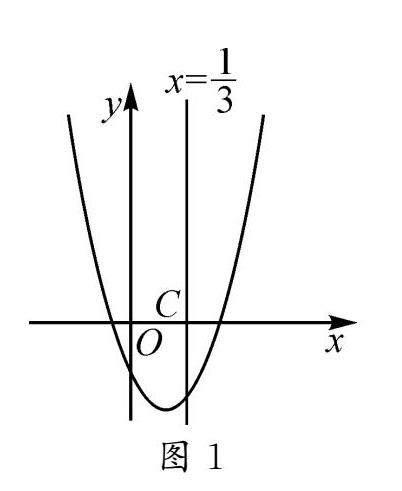
又如,学习了二次函数的图象和性质后,教师设计了这样一道练习:图1所示的是二次函数y=ax2+bx+c(a≠0)的图象,根据图象你能得到有关系数a,b,c的哪些关系和结论?
该题是一道“图象信息”开放题,重点考查学生对函数图象和函数性质的掌握情况.该题看似不难,但是需要学生具备一定的读图能力和灵活应用函数性质分析和解决问题的能力.只有学生熟练掌握函数性质,才能透过函数图象的表象挖掘出其中蕴含的所有关系和结论.在探索该问题时,教师应创造机会让学生互动,以此通过交流获得更多有价值的信息,培养学生读图能力,加深学生对函数性质的理解.
在课堂教学中,大多教师将时间和精力放在新知的讲授上,忽视了课后作业的设计,使得课堂作业的形式过于保守、单一,这样学生面对枯燥无味的课堂作业时难免会产生厌烦情绪,从而影响知识的巩固,抑制学生解题能力的提升.因此,在实际教学中,教师有必要在课后作业上下功夫,多为学生设计一些开放题,以此有效避免客观题的简单无趣,提升作业质量,促进知识的巩固和学生解题能力的提升.
俗话说:“众人拾柴火焰高.”在探索开放题的过程中,教师要充分发挥集体优势,提供机会让学生分享自己的思考过程和解题结果,从而让不同思维碰撞出耀眼的火花,有效激发学生学习兴趣,提高学生数学能力.
总之,在初中数学教学中,教师要根据教学内容和学情设计一些开放题,为学生营造一个自由探索的学习环境,让学生在数学的世界里自由翱翔,点燃智慧的火花,促进思维的发展和学习能力的提升,构建高效数学课堂.
