数学抽象理解及解题技巧
2024-06-21胡新华
胡新华


摘要:三角形是具有性质特征的最简单的几何图形,尽管图形是直观的,但将图象概括为数学概念却是一个抽象化的过程,因为三角形包含有边的长短、角的大小等“数字化”的要素.换句话说是将“形”转化为“数”的过程,是数学概念抽象概括的过程.“探索三角形全等的条件”就是对两个边长、角度一一对应的三角形,结合前面学过的线段和两角相等的知识进行探究,找出它们中一一对应的边、角相等的条件,是数学抽象理解与应用的过程.因此,在“探索三角形全等的条件”的课堂教学中,采用“实践活动中构建方法”的探究发现法最合适不过,既可以激活课堂气氛,又可以驱动学生的探究热情.
关键词:三角形全等的条件;抽象理解;解题技巧
“探索三角形全等的条件”是苏科版数学八年级上册第一章的内容,是继认识三角形之后,了解全等图形和全等三角形之后的知识拓展,体现了抽象的“数形转换”的数学基本思维方法[1].基于此,在课堂教学中,教师需要精心创设适合学生探究的教学情境,让学生自主在实践活动中得到原理和结论,亲历解决质疑情境问题的过程,从而构建释疑的方法,并内化为解决问题的基本技能、技巧.
1 创设实践案例,激发学生去思考
有人说“好奇是致胜的魔杖”,的确如此.好奇心强、探索心强是初中生的基本特征,根据这一点,教师可以创设能够吸引学生眼球的案例,引导学生存疑,再通过实践活动探究,找到释疑的途径.例如,在“探索三角形全等的条件”的课堂导入环节,可以这样精心创设情境.
师:教室后面的小组评比栏目需要进行周期性清理,然后重新记录评估,栏目中张贴的小红旗(纸质)不可能完整揭下来,需要重新用红纸剪裁出相同的小红旗(三角形).若某小红旗揭下来时,撕成下列三块,你认为用其中的哪些碎片就可以重新用红纸剪裁相同的小红旗呢?
教师课前给每位学生分发小红旗的碎片,如图1所示,让学生自己剪裁出小红旗的三块碎片.
学生选择不同的碎片进行探究,尝试利用不同的碎片或者碎片的组合重新用红纸剪裁相同的小红旗.
活动预案:取①②③中的一块碎片,不能用红纸剪裁出相同的小红旗(三角形),这说明只知道一个角相同时,不能确定两个三角形全等;取①②③中的任意两块碎片无缝对接,都能用红纸剪裁出相同的小红旗(三角形)(可以提醒学生注意,若有缝隙,或者碎片有部分重叠,则情况又会怎样?),这说明只知道两个角和其夹的一条边相同时,能确定两个三角形全等.
通过活动,教师及时.两个三角形的两边及其夹角相等时即全等,简称“ASA”.
创设目的:“用红纸剪裁相同的小红旗”的实践活动实质就是探究三角形全等条件的过程.开展这样的课堂活动,可以满足学生的好奇心和探究知识的欲望,在亲历尝试的过程中认知三角形全等的条件.因此,探究发现法的是利用学生的好奇心发现生成知识的过程,是求知欲的体现,是可以实现的目标[2].
2 设置经典问题,驱动学生去挑战
从八年级学生的学情可知,他们对几何知识的认知还是瘠薄的,部分学生对探究几何问题的方法、经验不足,达不到“数形转换”的思维水平,使得独立完成数学问题的探究成为空中楼阁.为了能让这部分学生迎头赶上,最有效的方法就是在课堂上生成新知之后及时设置课堂练习,通过小组合作的形式进行探究、交流,在活动过程中领会知识扎实的学生的思维方法,并内化为自己解决数学问题的能力.例如,在探索得到“两边及其夹角分别相等的两个三角形全等”后,要求学生分组探究这一基本事实的具体形式.
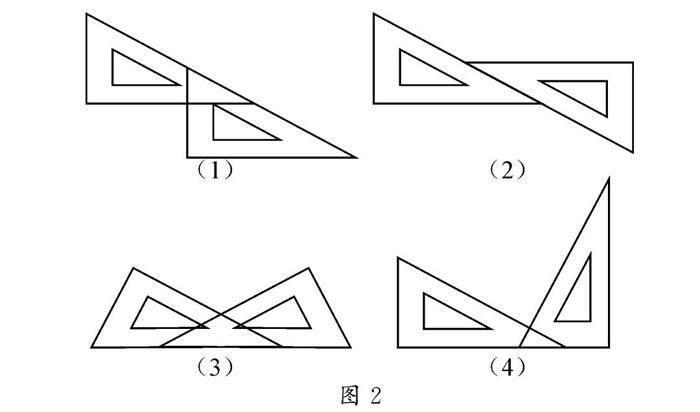
师:请同学们用两个相同的三角板,使其一边紧靠在一起,且不完全重合,观察这两个三角板的位置,编写一道利用本节课所学知识证明三角形全等的题,并写出证明过程.
生:用两个相同的三角板尝试满足教师设置的问题的要求,可以得出众多的位置.
活动预案:常见的两个相同的三角板位置形式如图2.
其中,用图2(2)的形式编写的数学证明题的成功案例如下:
如图3,在△ABC和△A′B′C′中,A,B,A′,B′四点在同一直线上.
证明过程都是利用课堂学习的新知:两边及其夹角相等的两个三角形全等,可以简称为“SAS”.
创设目的:通过用两个相同的三角板的组合位置,编写一道利用本节课所学知识证明三角形全等的题目的课堂活动是开放性的,因此采用了小组合作交流的方式.因为还未学习直角三角形的概念,不用考虑三角板的具体角度.课堂活动中,学生设计的两个三角板的位置是五花八门的,如图2中的(4),当然也可以编写其他数学问题,但已知条件就复杂得多,对学生应用知识的能力有更高的要求.因此,本活动采用小组合作探究的形式,有利于帮助学生克服探究过程中出现思维障碍导致无法独立解决的困难,同时,在合作中内化知识、优化构建、积累方法、激活思维、形成技巧.
3 内化生成知识,强化学生去拓展
课堂上学生对如何探究知识有了清晰的脉络之后,就需要将所获取的新知进行提炼与内化,真正了解数学问题的奥妙之处,这是课堂教学的重要环节,也是学生发展能力、形成学科素养不可或缺的组成部分.换句话说,就是驱动学生充分思考,获取感悟,深入探究,掌握技能方法.
如,可以采用近年的中考试题来内化所学的新知.
典例 (2021年福建中考题改编)如图4,已知D是BC的中点,F为AD的延长线上一点,作BE∥CF交AD于点E,求证:BE=CF.
学生根据已知条件找到△BED≌△CFD,即可得出BE=CF.
活动预案:在探究后的展示环节中,有学生给出这样的证明过程.
在△BED和△CFD中,因为D是BC的中点,故BD=CD;∠EDB=∠FDC;又由BE∥CF,得出∠DEB=∠DFC.所以△BED≌△CFD,故BE=CF.
展示之后有学生提出异议:本节“探究出的两个三角形全等的条件”是“ASA”,而该学生给出的却是“AAS”,两个三角形能全等吗?
于是,该学生进行反驳:因为三角形的内角和是180°,在△BED和△CFD中有两个角相等,那么,它们的第三个角必定也相等,因此“AAS”也可以作为判断两个三角形全等的条件.
创设目的:在探索问题的时候,初中生时常会力不从心,分类探讨时丢三落四是常见现象.因为他们正处于从直观思维到逻辑思维的过渡期,讨论问题时难免会出现思维跳跃等情况.本例旨在引导学生看问题时要注意养成全面思考的习惯,不断提升思维水平,进而内化成数学思维、数学能力、数学素养.
总之,只要在数学课堂教学中做到“创设实践案例,激发学生去思考;设置经典问题,驱动学生去挑战;内化生成知识,强化学生去拓展”,那么,数学抽象理解及解题技巧就会生根于学生的脑海中,内化成自身的素养[3].
参考文献:
[1]尚卫成,谭晓玲.初中数学核心素养“数学抽象”理解及解题技巧——以"探索三角形全等条件"为例[J].数学之友,2022,36(23):34-36.
[2]梁大胤.探索三角形全等条件案例分析[J].试题与研究(教学论坛),2021(1):122.
[3]魏凯,陈捷,张龙娟.基于数据采集与分析的课堂互动教学模式研究——以《探索三角形全等条件》一课为例[J].中国信息技术教育,2020(2):71-74.
