以问题为导向的初中数学结构化单元教学实践
2024-06-21王颖
王颖

单元教学是指将零碎的知识以结构化的方式进行整合或重组,从而形成完整的单元进行教学的一种方法.认知心理学家奥苏泊尔指出,建构知识的框架可以为学生的持续学习提供知识体系的支持,从而能够帮助学习者不断完善认知结构,提升学习能力.在结构化教学中通过问题引导的方式可以激发学生的生长点,拓展知识的延伸点,提升学生的核心素养[1].教学中将“中心对称图形——平行四边形中的‘菱形、矩形、正方形”这章内容以结构化的方式重新进行整合,本文中以“菱形、矩形、正方形的性质(1)”为例,探究初中数学结构化单元教学的实践.
1 温故知新,明确研究角度
问题1 我们已经研究过三角形的相关知识,你还记得研究三角形的路径吗?
追问:你能描述等腰三角形、直角三角形的概念吗?
问题2 平行四边形有哪些性质?我们是从哪些方面研究平行四边形的性质?
设计意图:本课从回顾三角形的研究路径出发,引导学生在回顾如何研究三角形的过程中逐步建构三角形的研究结构,形成如图1所示的结构图.在此基础上进行知识迁移,思考特殊平行四边形的研究路径,为学生自主归纳特殊平行四边形的概念提供条件.在回顾研究平行四边形内容的过程中,明晰平行四边形的研究角度,形成如图2所示的结构图.由此,为学生研究本课内容提供了方法指导,奠定了初步的思维基础.
问题3 根据你所知的研究三角形的路径,你认为我们接下来要研究平行四边形的什么内容?
追问1:你打算通过什么方法研究平行四边形的特殊性?
追问2:根据你的研究路径,动手画一画,可以得到什么特殊的平行四边形?
问题4 结合特殊三角形的概念,你能归纳出菱形和矩形的概念吗?
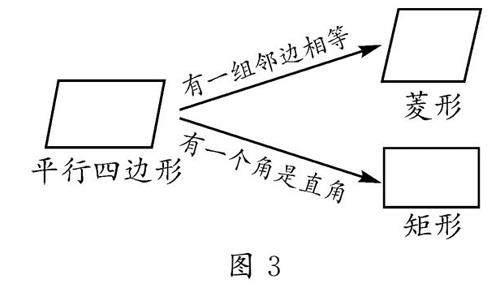
生:与等腰三角形的概念类比可得,有一组邻边相等的平行四边形是菱形;与直角三角形的概念类比可得,有一个直角的平行四边形是矩形.
设计意图:问题3引导学生明确需要研究的特殊平形四边形是哪些,以追问的方式,使学生类比研究特殊三角形的方法联想到从边和角的角度研究特殊的平行四边形.学生逐步掌握研究四边形的方法,同时
追问2培养学生动手操作、
推测想象和分析思考的能力,初步形成如图3所示的四边形研究框架图.
2 类比研究,初建知识结构
问题5 我们已经掌握了菱形和矩形的概念,你们还想了解这两种图形的什么内容呢?
生:按照研究三角形的角度,我们应该要继续学习这两种图形的性质.
追问1:菱形是特殊的平行四边形,它与平行四边形的性质有哪些异同点?
追问2:你能够从哪些角度研究菱形的特殊性质?
生:我是从边、角以及对角线的角度进行研究.
追问3:你是如何想到这些研究角度的?
生:我从研究平行四边形的结构图中类比得出的.
追问4:想一想菱形有哪些特殊的性质?小组讨论交流后进行总结并展示,并说明理由.
设计意图:本环节教师采用类比的方法,引导学生明确了解图形的概念之后需要继续研究图形的性质.在追问中引导学生将菱形的性质与平行四边形的性质进行联系,并通过比较让学生明确菱形特有的性质.教师通过追问引导学生反思研究的角度,养成探究问题本质的习惯,最后通过小组活动,合作交流,建立菱形性质的知识结构,在抽丝剥茧的问题中发展数学思维能力,积累活动经验,掌握数学的研究方法[2].
问题6 刚刚我们已经掌握了研究菱形的过程,下面请同学们通过自主探究,总结矩形的性质,并与小组同学交流.
生:矩形也属于平行四边形,我们同样可以从边、角、对角线等角度进行研究.
设计意图:本环节从知识迁移的角度引导学生类比菱形的性质,研究矩形的性质,帮助学生形成系统的知识结构,从而渗透结构化思维,使学生不仅能够知其然,还能知其所以然,掌握研究问题的方法,发展核心素养.
3 精选试题,提升应用能力
问题7 我们已经探究了矩形和菱形的性质,那么如何在实际问题中加以应用呢?
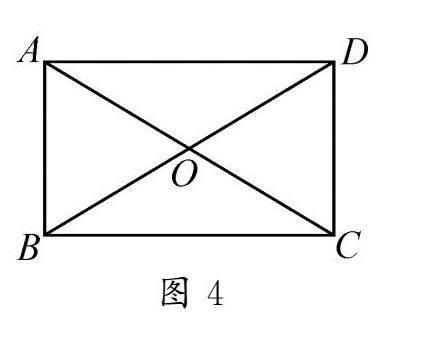
(1)如图4,AC,BD为矩形ABCD的对角线,交于点O.
①若∠ACB=30°,AB=3,求AC的长度.
②若∠AOD=120°,AB=3,求AC的长度.
生:①根据矩形四个角为直角可知∠CAB为60°,矩形的对角线相等且互相平分,因此△AOB为等边三角形,可得AC的长度为6.同理可解决第②问.
(2)如图5,已知菱形ABCD的对角线相交于点O.
①若AC,BD的长度分别为6 cm和8 cm,求菱形的边长.
②若菱形ABCD的周长为52 cm,BD=24 cm,求AC的长度.
生:①根据菱形的对角线相等并且相互垂直,可以应用勾股定理求得菱形的边长为5 cm.同理,应用菱形的边长相等,可以解决第②问.
设计意图:本环节通过两个问题的设计分别考查了矩形的角和对角线的性质以及菱形的边和对角线的性质,提升了学生灵活运用知识的能力,巩固了对这两个图形性质的掌握.学生在掌握概念、性质等知识的基础上,在实际问题中进行知识的运用,有助于将知识融入到实际问题当中,提升应用思维能力.
4 总结归纳,深度融合升华
问题8 回顾本课的学习,我们从哪些角度研究矩形和菱形的概念和性质?请你总结研究几何图形的具体路径.
生:本课我们主要研究了矩形和菱形的概念和性质,在研究过程中我们首先通过类比三角形的研究结构得到平行四边形的研究路径,进而借助平行四边形的研究角度得到研究矩形和菱形的性质.因此我们可以总结研究几何图形的路径是从概念到性质进而判定.
设计意图:通过问题引导学生回顾研究的过程,帮助学生建立知识结构,实现新旧知识的联系和顺应.回顾研究的路径,使学生将研究方法进行知识迁移,锻炼了数学思维,为接下来进一步学习正方形以及判定特殊平行四边形提供了方法指导.
问题9 我们学完菱形和矩形之后,还会继续研究什么四边形呢?
设计意图:通过问题引导学生在已有知识基础上展望接下来的学习,从而帮助学生从整体上感知单元知识,形成完整的知识结构,图结构图(4),同时学生实现了研究方法的延续和迁移,由此掌握了研究该类问题的方法结构.
作业设计:回顾本课研究过程,请你仿照本课研究菱形和矩形的研究方法,自主探索正方形的概念和性质.
设计意图:课后自主探究正方形一方面能够使学生复习巩固研究四边形的方法,同时也能让学生在具体问题中应用结构化思维,提升学生的思维能力,使学生不仅掌握数学知识,更能掌握学习方法,真正实现“教”是为了“不教”的目的.
4 教学反思
4.1 关注逻辑结构,落实核心素养
结构化单元教学以课标为依据,以教材为载体,根据单元内部知识之间的联系进行内容整合,从而建立起同类研究方法和研究路径的知识结构,使学生能够形成前后逻辑连贯的学习思想,发展数学核心素养.
本课从类比三角形的研究路径出发,将研究方法迁移到平行四边形的研究中,并形成整体单元研究的知识结构.从特殊三角形的概念到菱形和矩形的概念,从平行四边形的性质到菱形和矩形的性质,从一般图形到特殊图形,都体现了前后相连、内在联系的逻辑结构,在学生的头脑里形成研究三角形、平行四边形以及矩形和菱形的知识结构[3].
结构化单元教学追求的是单元的整体视角和连贯的逻辑,学生在问题的引导下将各种知识建构起网络,并在研究图形的过程中形成系统的思维.
4.2 问题引导实施,升华数学认识
结构化单元教学在具体实施的过程中,一般是按照初步整体感知单元、具体深入分析知识点、揭示内在联系、深度融合与升华的步骤展开的.
从数学思想的角度,本课通过由浅入深的问题引导学生关注知识的整体性,如要求学生回顾三角形的研究角度,从而建构平行四边形的研究结构图.在总结归纳阶段引导学生回顾研究过程,形成本单元的知识结构,由此形成数学思想上的整体性和系统性.
从学习内容的角度,由概念学习到问题引导学生思考还能研究哪些内容?哪些图形?不断完善知识结构,由此体现了初中数学知识内在的联系,比如按照从角到三角形、四边形再到圆的过程来学习平面几何图形.
综上所述,结构化单元教学就是以结构化的形式将零散的知识联系起来,与学生头脑中原有的知识结构进行关联,从而不断完善已有认知结构,提升学生的认知能力.教师要依据“课标”对教材内容进行结构化研读,厘清知识之间的逻辑关系,发现教材内容的核心价值,在教学中以问题的形式渗透核心素养,从而发展学生的数学思维.
参考文献:
[1]章建跃.研究三角形的数学思维方式[J].数学通报,2019,58(4):1-10.
[2]章飞.单元教学的核心思想与基本路径[J].数学通报,2019,58(10):23-28.
[3]吴亚萍.中小学数学教学课型研究[M].福州:福建教育出版社.2014.
