借助思维训练，摆脱初中数学解题困境

王慧

【摘要】数学是初中教育阶段的一门重要课程，知识难度与深度同小学相比有明显提升，跨度较大，相应的试题难度也有所增加.学生在解题过程中会遇到不少困难，究其原因大部分时候都是思维受到限制，教师应有意增强思维训练，帮助学生摆脱解题困境.本文主要对如何借助思维训练摆脱初中数学解题困境进行研究，同时罗列出部分解题实例.

【关键词】思维训练；初中数学；解题技巧

从字面意思看，思维就是人脑通过语言对事物进行概括与间接反应的一个过程，通俗来讲，就是人们所说的“思考”，在思考中的“想”就是思维过程.在初中数学解题训练中，当学生碰到认为自己无法解决的难题时，思维将会陷入瓶颈，停滞不前，这时就要给予思维点拨或者指导，通过思维训练让学生的思维“动”起来，使其顺利摆脱数学解题的困境.

1 精心设计一题多解，训练学生灵活思维

在初中数学解题教学中，不少题目设计思路关注考查学生的思维是否灵活，试题内容新颖、个性，且能够采用多种不同的方法完成求解，学生应拥有牢固的知识基础做铺垫，从而做到灵活解答试题.对此，初中数学教师可精心设计一题多解练习活动，让学生使用不同方法解答同一题目，使其灵活使用所学知识，让学生思维变得更为灵活［1］.

例1 在图1中，有一个△ABC，D点是AC边上的一点，其中CD=2AD，E点是BD的中点，然后对AE进行延长，与BC边相交于F点，那么BF与FC之间的比值是多少？

解法1 依托三角形中的中位线定理与平行线性质

过点D作辅助线DN∥AF，DN与BC边相交于点N，如图2所示.

因为E点是BD的中点，

依据三角形中位线定理可知F点为BN的中点，

又因为DN∥AF，

所以CN∶NF=CD∶DA=2∶1，

由此得到CN=2FN=2FB，

则BF∶FC=1∶3.

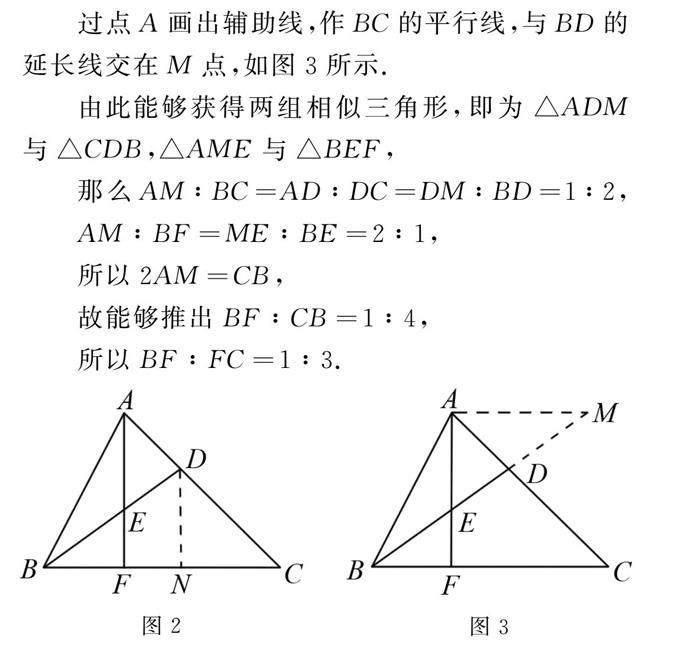
解法2 借助相似三角形性质

过点A画出辅助线，作BC的平行线，与BD的延长线交在M点，如图3所示.

由此能够获得两组相似三角形，即为△ADM与△CDB，△AME与△BEF，

那么AM∶BC=AD∶DC=DM∶BD=1∶2，

AM∶BF=ME∶BE=2∶1，

所以2AM=CB，

故能够推出BF∶CB=1∶4，

所以BF∶FC=1∶3.

2 巧妙开设一题多变，训练学生批判思维

同一题多解相反的是一题多变，前者指的是一道题目有多种解法，后者发生变化的则是题干信息，以一道常规题目为发起点变化出多道试题.针对初中数学解题教学，为训练学生的思维能力，教师便可巧妙开设一题多变方面的解题训练，带领学生面对多道类似问题展开深层次的研究和探索，使其真正理解试题的本质所在，实现对学生批判思维的训练［2］.

例2 已知函数y=（3-a）x-2a+18是一个一次函数，那么a的具体范围.

详解 因为y=（3-a）x-2a+18是一个一次函数，

所以3-a≠0，

解得a≠3，

所说a的具体范围是a≠3.

接着，教师可以原题目为基础安排变式练习，且提升变式的难度.

如：（1）已知函数y=（3-a）x-2a+18是一个一次函数，如果该函数图象经过原点，求a的取值范围.

（2）已知函数y=（3-a）x-2a+18是一个一次函数，且该函数图象和y轴的交点在x轴的下面，请求出a的具体范围.

（3）已知函数y=（3-a）x-2a+18是一个一次函数，y随x的增大而变小，求a的具体范围？

这些变式主要考查学生对一次函数图象的规律、性质等掌握情况，还对他们的空间想象能力有着一定要求，使其通过批判性思考顺畅完成解题.

3 合理引入一题多思，训练学生缜密思维

在初中数学解题训练中，学生应具备一定的推理能力和逻辑思维，尤其是当处理部分难度系数较大的试题时，他们需拥有缜密的思维才能够摆脱困境.为此，初中数学教师在平常解题训练中可合理引入一题多思活动，引导学生在解题过程中多多进行思考，使其能够把隐性信息给挖掘出来，归纳题目规律，让学生的思维变得更为缜密，提升解题效率［3］.

例3 如图4所示，在△ABC中，∠B=2∠C，∠BAC的角平分线AD与BC相交于点D，请证明AB+BD=AC.

证明 在边AC上取一点E，使AB=AE，

在△ABD和△AED中，AB=AE，

∠BAD=∠EAD，AD是公共边，

故△ABD≌△AED，

所以∠B=∠AED，BD=DE，

又因为∠B=2∠C，

所以∠AED=2∠C，

因为∠AED是△EDC的外角，

所以∠EDC=∠C，

故ED=EC，

则BD=EC，

所以AB+BD=AE+EC=AC.

4 突破固有解题束缚，训练学生逆向思维

对于初中数学解题教学而言，一些题目比较特殊，采用正向思维解题难度较大，即便可以求得结果，但是过程十分复杂.教师可以提示学生转变思维方向，基于逆向视角切入，从题设结论往回倒着推理，通过逆向思考与分析找到解题的切入点，形成简洁的解题思路，使其摆脱固有解题思维的束缚，从而让学生学会对逆向思维的高效实用.

例4 证明：无论k为何值时，有关x的方程x2+x（k+2）+2k-1=0存在2个不一样的实数根.

证明 假设无论k为何值时，该方程不存在2个不一样的实数根，

因为x2+x（k+2）+2k-1=0，

所以该方程的根的判别式是Δ=k2-4k+8，

配方以后能够得到Δ=（k-2）2+4，

故k的值不会影响到判别式是正、还是负，

也就是该方程不存在2个不一样的实数根是不成立的，

所以题设成立.

5 结语

总而言之，在初中数学解题训练实践中，教师不能拘泥于常规，除做好理论知识讲授与常规解题方法练习外，还要注重思维能力的训练，通过创新解题教学方式促进学生学习灵活、批判、缜密与逆向思考，使其思维能力变得越来越强，帮助学生真正走出解题困境.

参考文献：

［1］朱晶晶.初中学生数学解题中的思维障碍研究［J］.数理天地（初中版），2023（13）：31-32.

［2］林洁华，梁建新.浅析提高初中学生数学解题能力的有效途径［J］.考试周刊，2023（30）：82-85.

［3］赵静静.发展学生思维能力 提升数学解题效率［J］.数理化解题研究，2023（20）：53-55.