用数组模型解决“移拼倒三角形”问题

殷素文

［摘  要］ 文章以棋子移动为例，把生活中貌似复杂错乱的图形变化题，用数组模型的方法进行解答，使之既有序又简约，更好地体现用数学模型解题的高效性和优越性，从而培养、激发学生的模型意识，提升学生的数学核心素养。

［关键词］ 数学模型；数组；转化

小学数学苏教版五年级下册“解决问题的策略”把两种典型的数列求和问题运用转化的策略进行教学，即把等差数列转化成梯形，把等比数列（比值是0.5）转化成正方形。这两种转化的策略是由数到图的典型应用，属于计算技巧的类别。现实生活中经常遇到由文字表达或图形呈现出的问题，探寻这些问题背后的数学模型，实现由图到数的思维提升，可以助力学生更高效地解决问题。

一、网络小视频，问题在身边

网络小视频有一道题：如图1（1），请在10秒内，只移动3颗棋子，使图形变成倒三角形。解题图示见图1（2）。

很多网友挑战失败，在解题过程中棋子既有上移又有下移，容易干扰思维。当多次刷到这个视频时，笔者逐渐产生以下想法：

①這只是一道简单的棋子移动问题吗？可不可以用数学方法来解决？

②最少只需要移动3颗棋子吗？

③如果是一个5层、6层以及更多层结构的三角形，最少需要移动多少颗棋子？

④这种研究方法对于其他图形有没有通用性？

带着这样的问题，笔者开始了“移拼倒三角形”背后的数学模型的探究。

二、过程再还原，有序更清晰

《福尔摩斯探案》是受青少年喜爱的侦探小说之一，当案件侦破遇到困难的时候，探员便使用“现场还原”技法进行案件侦破，并屡试不爽。“重回”案发现场，有助于从源头剖析案件各要素特点、逻辑关系以及推测事件进展的可能性［１］。同样，在研究“移拼倒三角形”过程中，笔者以网络视频中的4层结构三角形为例，还原移拼过程，以利于观察其中的变化规律，抽丝剥茧，进而提炼问题背后的数学方法。

因为研究需要移动的最少棋子数，就一定存在不需要移动的最大棋子数，也就是移动前与移动后的两个三角形存在最大的重叠棋子数，这样就只需要观察两个三角形可能存在的不同位置情况，并结合这些情况，用合理的数学模型来研究棋子的移动情况，这样研究起来就要理性、快捷得多。

图2中，用实心圆表示原来的三角形，用空心圆表示移动后的倒三角形。两个三角形先用棋子数为4的2层重叠，然后倒三角形逐层上移，直至棋子数为1的2层重叠。两个三角形的重叠部分表示不需要移动的棋子，剩下的实心圆数量就是需要移动的棋子数量。图2（1）到图2（7）中重叠部分的棋子数分别为4、6、7、6、4、2、1颗，则需要移动的棋子数分别为6、4、3、4、6、8、9颗。不难发现，图2（3）中重叠棋子数最多，同时也是需要移动棋子数最少的，只需要移动3颗棋子。图形分析到这里好像已经找到了最少移动棋子的方法，但这种方法无疑会消耗学生较多的时间和精力，虽简单但无趣。

三、数组作模型，简易又形象

《孙子算经》认为数学是天地万物最根本的东西。现代社会的一切信息都可以用“数字化”来表示和加工，推动现代社会进步的也是一系列的数据计算［２］。那么“移拼倒三角形”问题必然可以用数学的方法来探究背后的奥秘。

根据三角形棋子的空间形式和数量关系，可以把移动前的三角形棋子分布抽象得出数组，移拼后的倒三角形也可以表示为数组，接下来只要研究两个数组在重叠层数不同的情况下，重叠的棋子数及需要移动的棋子数，问题就简单多了。图2的7种情况可以用7个新的数组来表示（如图3）：

图3中每个新数组的左列数据表示原来的三角形棋子，右列表示移拼后的倒三角形棋子。当同一行中两列数据都出现，说明两个三角形有重叠的部分，重叠数的大小取两个数据中的较小数。同一行中，当左列数据比右列数据大，说明多出的棋子数就是原三角形需要移动的棋子数。如图3（1）中第一、二、三行（从上往下数，下同）左列数据比右列大，需要移动的棋子数就是：1+2+3=6（颗），图3（5）中，第四、五行左列数据比右列大，需要移动的棋子数就是：3-1+4=6（颗）。这样一来，研究“移拼倒三角形”问题就转化成两个数组在重叠层数不同的情况下，同一行中左列数据大于右列数据的情况，再进行求和，这样，思维效率就提高了很多。

从图3中可以得出：4层结构的三角形移拼成倒三角形，当重叠层数为3时，需要移动的棋子数是：1+4-2=3（颗），最少。因为从图3（5）开始，同一行中左列数据大于右列数据是增加趋势。因此，在图3中，分析4层结构的“移拼倒三角形”问题，当重叠层数达到4层时，后面的情况可以排除，不再分析。

接下来用数组模型研究5层结构的“移拼倒三角形”问题中出现的情况及最少移动棋子数。

从图4（3）可以得到，需要移动的棋子数为：1+2+5-3=5（颗），图4（4）中需要移动的棋子数为：1+4-3+5-2=5（颗），结合图形可以确定，这两种方法都是移动棋子数最少的，棋子的实际分布情况如图4（6）和图4（7），数组模型的结论符合实际情况。

四、数据重整合，效率再提高

数学研究的特点之一是可以进行算法优化，即在获取新的知识或技能后，可以重新组织已有的知识结构使之不断改善自身的性能，实现对数据模型的优化重建。

为了更快地探究不同重叠层数时需要移动的棋子数，对图4（1）到图4（5）的数组进行重建。通过观察不难发现，可以将左边的数列看作是固定的，将右边的数列看作是自下而上的移动，把不同情况的右列数合并在同一数组中，得到图5。

图5中带圆圈的数字表示通过计算后需要移动的棋子数，用这种数组重建的简化方法把求解的效率提高了很多。这种用数组的方法解答“移拼倒三角形”问题很容易推广到6层、7层等结构的三角形。

五、由数回到图，呈现方完美

从上面的数组分析，可以快速得到原三角形与倒三角形存在的重叠层数，以及需要移动的棋子数。笔者以图4（4）的情况为例，示范由数组回到图形，给出最终移动棋子的方法。

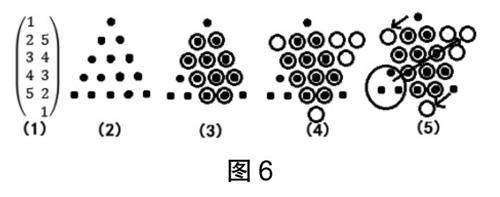
图6（1）是两个三角形的数组模型。在原来的三角形图6（2）中，首先，根据同一行中左列数据比右列数据小，说明左列该行棋子不要移动的原理，圈出图6（3）中的上面第2、3层；其次，根据右列数据比左列数据小，说明右列该行只要这几颗棋子，且尽量居中，呈逐步收缩状排布，圈出图6（3）中的下面2层；第三，根据最终倒三角形棋子的排布，补充出倒三角形需要的棋子，如图6（4）中的空白圆圈；最后，对照原三角形多出的棋子和倒三角形需要补充的棋子，进行移动，最终得出移拼的结果，如图6（5）。

至此，用数组模型解决“移拼倒三角形”问题已全景呈现，这种应用是对图形中数据的抽象与提炼，是图形到数学模型的转化。

六、追根溯源，问题背后的问题

在探究“移拼倒三角形”问题的时候，通过逆向推导发现决定最少移动棋子数的关键变量是两个三角形的重叠层数，即重叠层数决定重叠的棋子数，重叠的棋子数决定需要移动的棋子数。虽然重叠层数是一个变量，总存在着一个重叠层数，可以导出最少的移动棋子数，但图4（6）和图4（7）的情况又与这一结论相悖，因此这一问题的背后一定关联着一个更深或暂且未知的问题。

联想到正弦函数图象及函数极值相关的内容，图4（6）和图4（7）的重叠层数相等，说明这两种情况应该是极值两端的某个相等值，就像图2（2）与图2（4）或图2（1）与圖2（5）。难道5层结构的三角形重叠层数应为3.5（或为其他小数）层？但三角形棋子分布中，3.5层就是中间的空格地带。

仔细推敲一下，人们平时表述的三角形是一个密铺的图形，中间不存在空域。三角形棋子分布只是完整三角形的抽象表达，这样一来整个问题就清晰了：三角形棋子是被局限于整数的原三角形的抽象表达，“移拼倒三角形”问题的原型是两个三角形的最大重叠面积问题。最大重叠面积导致非重叠面积最小，最大重叠面积又是由某个重叠高度所决定，只不过这个重叠高度在一般三角形里表现为唯一值，在三角形棋子中可以表现为这个重叠高度的两个相邻整数。至此，“移拼倒三角形”问题完成了“认祖归宗”。

当然，如果设定参数，用方程或通过编程的方式也能解决倒三角形的移拼问题，在小学阶段暂且探究到这个程度。用数组模型解决“移拼倒三角形”问题的重要性在于：这种思维方式能够培养学生用数学的眼光观察身边事物的习惯，培养学生的模型意识，提高学生用数学模型解决问题的能力，提升学生的数学核心素养。

参考文献：

［１］ 宗晓荣. 试析小学数学教学中数学模型思想的融入［Ｊ］. 天津教育，２０２０（１１）：１７６－１７７.

［２］ 柯黎青. 小学数学教学中融入模型思想的探讨［Ｊ］. 考试周刊，２０１９（１３）：８９.