JAVA稀疏矩阵算法

陈新龙

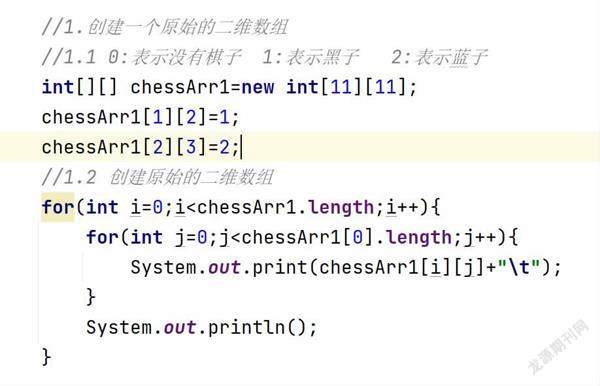
假设我们要编写一个五子棋的程序，过程中需要考虑保存黑棋和白棋的位置，这个时候你会用什么样的解决方法呢？相信很多人第一时间想到的肯定是二维数组（Array[x][y]），因为二维数组本质上是以数组作为数组元素的数组。数组的X坐标正好对应棋盘上的X轴，Y坐标正好对应棋盘上的Y坐标，例如图1中黑色棋子的位置就是（1，2），蓝色棋子的位置就是（2，3）;将对应棋盘中的棋子通过数字的形式存入到二维数组中，0代表不存在任何数字，1代表黑色棋子，2代表蓝色棋子（图1）。

虽然通过二维数组的方法可以保存棋盘的位置，但是保存过程中会出现一个问题，比如数组中的0太多了，因为二维数组中很多值都是默认值0，如果把这些0记录下来就会产生很多没有意义的数组，为了解决重复性的问题，我们可以考虑使用稀疏矩阵数组来解决问题。

什么是稀疏矩阵呢？矩阵是一个由m行和n列组成的二维数据对象，因此一共有m×n个数值。当这个矩阵的绝大部分数值为零，且非零元素呈不规律分布时，则称该矩阵为稀疏矩阵。如上图就是一个11×11的稀疏矩阵，由于稀疏矩阵含有许多数值为零的元素，我们可以运用特定算法做很多重要的事情：比如压缩矩阵对象的内存空间、加速多数机器学习程序等。

存储稀疏矩阵时在普通情况下必须为矩阵中的每个零值位点分配32位乃至64位存储器，这明显是过于浪费内存资源的行为，因为这些零值不包含任何信息。我们可以利用压缩技术使我们需要存储的数据量最小化。稀疏矩阵中有很多零值，我们也知道零乘以任何数还是零，如果依然按照常规办法计算机就会不可避免地进行很多无意义的运算，大大拖延了处理时间。显然，只操作那些返回非零数值的元素才是更加有效率的办法。而稀疏矩阵数组正可以将无意义的零值从运算中剔除出去，因此，任何用到基本数学运算（比如乘法）的算法都能从稀疏矩阵实施中获益。

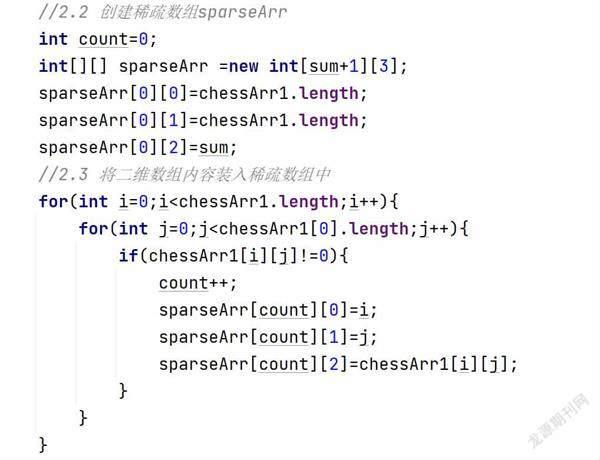
当一个数组中大部分元素为0，或者为同一个值的数组时，可以使用稀疏数组来保存该二维数组。其实稀疏数组的处理方法并没有多么复杂。首先需要记录数组一共有几行几列，并记录数组中一共有多少个不同的数字，其次把不同数值的元素和行列及值记录在一个更小规模的数组中，从而缩小程序的规模。当然这个过程是可逆的，还可以通过稀疏数组还原成原始的二维数组（图2）。

创建一个原始的二维数组（11×11）并给数组中的所有元素赋予初始值0，将棋盘上的黑棋和蓝棋的坐标表示在二维数组中（0：表示没有棋子;1：表示黑棋;2：表示蓝棋）。通过遍历原始的二维数组，我们可以得到有效数据的个数并存入sum中。根据sum的个数可以创建稀疏数组sparseArr int[sum+1][3]。你可能会奇怪sparseArr稀疏数组中Y坐标的值为什么是3，其实这个数字3代表的是row【横坐标】、col【纵坐标】、val【数值】，存放有效数据的数据坐标。通过遍历的方式将有效的数据存入到稀疏数组中即可。

下面给大家展示一下代码核心部分，有兴趣的同学还可以思考一下从稀疏数组转换为原始的二维数组的过程哦（图3、图4）。

當然稀疏数组不仅仅适合用在五子棋中，扫雷、围棋等一系列无效数据较多或矩阵中也可以用，你还能不能举出稀疏数组的案例呢？