广义θ-图和广义梅花图φ的奇异性

马海成, 攸晓杰

(青海民族大学 数学与统计学院, 西宁 810007)

1 引言与预备知识

本文仅考虑有限无向的简单图. 设G是一个n阶图, 它的邻接矩阵A(G)=(aij)n×n定义为

显然,A(G)是一个对角线元素均为0, 其他元素为0或1的实对称矩阵, 其特征值都是实数.A(G)的特征值也称为图G的特征值, 图G的n个特征值构成的全体称为G的谱.在图G的谱中, 非零特征根的个数和零特征根的个数分别称为图G的秩和零度, 分别记为r(G)和η(G), 显然r(G)+η(G)=n.

在化学中, 用图可以表示一个共轭烃分子, 称为分子的分子图.分子图的零度(或秩)在化学中有重要应用[1-6].例如: 图的零度等于0是其所表示分子化学性质稳定的一个必要条件[6].Collatz等[2]提出了刻画所有零度大于零的图问题.如果一个图有0特征值, 即η(G)>0, 则称其为奇异的.文献[2]提出的问题相当于刻画所有奇异图的问题, 是一个非常难的问题.为研究该问题, 已得到了零度(或秩)与图结构之间的许多结果[7-17].

奇异图有许多等价的定义, 一个图是奇异的当且仅当其邻接矩阵的核空间不是零空间; 一个图是奇异的当且仅当以邻接矩阵为系数矩阵的齐次线性方程组AX=0有非零解.文献[18-22]从这个角度研究了图的奇异性, 给出了一个图是奇异图的许多必要条件和充分条件.一个图是奇异的当且仅当存在一个非零的向量X=(x1,x2,…,xn), 用该向量对图上的点赋权, 每个点u∈V(G)满足

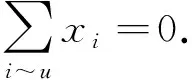
(1)

图1给出了格子图P5×P5和完全二分图Km,n满足式(1)的点上的赋权, 表明格子图P5×P5和完全二部图Km,n(m+n≥3)都是奇异的.

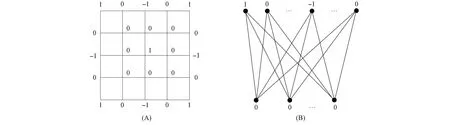
图1 格子图P5×P5(A)和完全二部图Km,n(m+n≥3)(B)上满足式(1)的一种赋权Fig.1 A kind of weight that satisfy equation (1) on lattice graph P5×P5(A) and complete bipartite graph Km,n(m+n≥3) (B)

一个图是奇异的当且仅当其邻接矩阵是奇异的, 即其邻接矩阵的行列式的值为零.基于此, 文献[23-24]给出了几类三圈图奇异的充分必要条件和这些图中奇异图发生的概率.文献[25-28]研究结果表明, 奇异图与数学中有限群的表示理论、 组合数学、 代数几何等均有联系.本文考虑广义θ-图和广义梅花图φ奇异的充分必要条件, 以及其中奇异图发生的概率.

用Pn和Cn分别表示n个点的路和圈.分别连结k条路Pa1+2,Pa2+2,…,Pak+2的起点和终点得到的图称为广义θ-图, 记为θ(a1,a2,…,ak), 这里ai≥0(i=1,2,…,k)且它们中最多有一个为0.连结k条路Pa1+1,Pa2+1,…,Pak+1的起点和终点为一个点得到的图称为广义梅花图, 记为φ(a1,a2,…,ak), 这里ai≥3(i=1,2,…,k).广义θ-图θ(a1,a2,…,ak)和广义梅花图φ(a1,a2,…,ak)如图2所示.用G∪H表示两个图G和H的点不交并图.度数为1的点称为悬挂点, 与悬挂点相邻接的点称为拟悬挂点.本文未说明的记号和术语可参 见 文 献[1].

引理2[1]设图G有一个悬挂点,H是从图G中删除该悬挂点以及和它邻接的拟悬挂点后得到的图, 则η(G)=η(H).等价地, 图G非奇异当且仅当图H非奇异.

每个分支都是孤立边或圈的图称为基本图.图G的包含所有点的基本子图称为图G的基本支撑子图.仅有孤立边组成的基本支撑子图称为图G的完美匹配.显然, 带有完美匹配的图的点数一定是偶数.

引理3[1]设G是n个点的图, 其邻接矩阵为A(G), 则

这里H表示图G的所有基本支撑子图构成的集合,p(H)表示H中分支的数目,c(H)表示H中圈的数目.

2 主要结果

定理1广义梅花图G=φ(a1,a2,…,ak)是奇异的当且仅当下列情形之一成立:

1)G的偶长圈多于一个;

2)G恰有一个偶长的圈, 且该圈的长为4的倍数;

3)G没有偶长的圈, 且长模4余1的圈和长模4余3的圈各占1/2.

证明: 设G=φ(a1,a2,…,ak), 图G可能的基本支撑子图有两类: 一类由一个圈和一些孤立边组成; 另一类由孤立边组成, 即完美匹配.

1) 图G的偶长圈多于一个, 此时图G没有基本支撑子图, 由引理3知,G是奇异的.

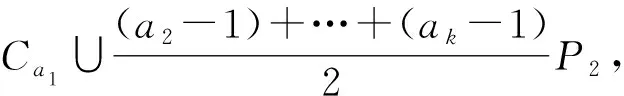
(-1)[(a2-1)+…+(ak-1)]/2+1×2+(-1)[a1+(a2-1)+…+(ak-1)]/2×2=0,

(2)

将式(2)两边乘以(-1)[a1+(a2-1)+…+(ak-1)]/2, 当且仅当(-1)a1/2=1, 当且仅当a1是4的倍数.

将式(3)两边乘以(-1)[(a1-1)+(a2-1)+…+(ak-1)]/2, 当且仅当

(-1)(a1-1)/2+(-1)(a2-1)/2+…+(-1)(ak-1)/2=0,

当且仅当数字a1,a2,…,ak中, 模4余1和模4余3的数各占1/2.证毕.

定理2设A={a1,a2,…,ak}是一些大于等于0的整数组成的可重集, 且其中最多只有一个0, 广义θ-图θ(a1,a2,…,ak)是奇异的当且仅当下列情形之一成立:

1) 集合A中没有奇数, 且模4余0和模4余2的整数各占1/2;

2) 集合A中只有1个奇数, 且其余的数中模4余0和模4余2的整数各占1/2;

3) 集合A中只有2个奇数, 且这两个奇数关于模4同余;

4) 集合A中多于2个奇数.

证明: 设G=θ(a1,a2,…,ak), 图G可能的基本支撑子图有两类: 一类由一个圈和一些孤立边组成; 另一类由孤立边组成, 即完美匹配.

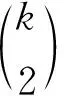
(-1)(a3+a4+…+ak)/2+1×2+(-1)(a1+a4+…+ak)/2+1×2+…+(-1)(a1+a2+…+ak-2)/2+1×2+

(-1)[(a1+2)+a2+…+ak]/2+(-1)[a1+(a2+2)+…+ak]/2+…+(-1)[a1+a2+…+ak-1+(ak+2)]/2=0,

(4)

将式(4)两边乘以(-1)(a1+a2+…+ak)/2+1, 当且仅当

[(-1)(a1+a2)/2+(-1)(a1+a3)/2+…+(-1)(ak-1+ak)/2]×2+k=0,

当且仅当

当且仅当(e-f)2=0, 当且仅当e=f.

2) 集合A中只有1个奇数, 不妨设a1是奇数, 集合A中模4余0的整数有e个, 模4余2的整数有f个,e+f=k-1.图G的基本支撑子图只有一类, 即奇数路和其中的另一条路(包括θ的两个端点X,Y)构成一个圈, 其余路上的点构成完美匹配, 这样的基本支撑子图共有(k-1)个.于是由引理3知,θ(a1,a2,…,ak)奇异当且仅当

(-1)(a3+…+ak)/2+1×2+(-1)(a2+a4+…+ak)/2+1×2+…+(-1)(a2+a3…+ak-1)/2+1×2=0,

(5)

将式(5)两边乘以(-1)(a2+…+ak)/2+1, 当且仅当

(-1)a2/2+(-1)a3/2+…+(-1)ak/2=0,

当且仅当数字a2,a3,…,ak中模4余0和模4余2的整数各占1/2.

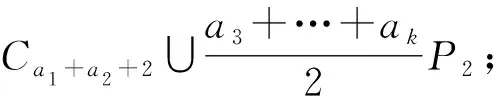
(-1)(a3+…+ak)/2+1×2+(-1)[(a1+1)+(a2+1)+a3+…+ak]/2×2=0,

(6)

将式(6)两边乘以(-1)[(a1+1)+(a2+1)+a3+…+ak]/2, 当且仅当(-1)(a1+a2)/2+1=0, 当且仅当数字a1,a2模4同余.

4) 集合A中多于2个奇数.此时图G没有基本支撑子图, 由引理3知, 图G是奇异的.证毕.

定理3设随机给定一个图G=φ(a1,a2,…,ak)是奇异图的概率为p, 则

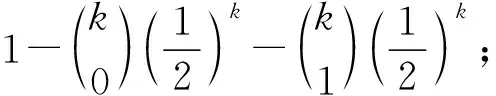
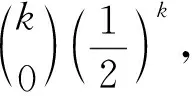
证毕.

定理4设随机给定一个图G=θ(a1,a2,…,ak)是奇异图的概率为p, 则

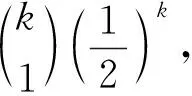
于是由定理2知,

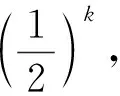
证毕.

文献[25]给出了单圈图、 双圈图以及部分三圈图奇异的判别方法, 如一个圈Cn是奇异的当且仅当4|n.图θ(a1,a2,…,ak)(或φ(a1,a2,…,ak))的某些点上长出一些树, 即若干棵树上的根点和图θ(a1,a2,…,ak)(或φ(a1,a2,…,ak))上的某些点粘结后得到的图的集合记为T(θ)(或T(φ)), 重复使用引理2, 即删除图上的悬挂点和拟悬挂点, 利用定理1、 定理2、 引理1和引理2, 可以确定T(θ)(或T(φ))中的奇异图.