轮图的平衡性

李诗雅，马晓玢

(安徽理工大学数学与大数据学院，安徽 淮南 232001)

0 引言

本文只研究无重边无环的简单图.记G=(V(G),E(G))是一个顶点集和边集分别为V={v1,v2,…,vn}和E=E(G)的n阶简单图.图G的邻接矩阵A(G)=(aij)n×n，其中，若vi,vj相邻，则aij=1；否则aij=0.邻接矩阵A(G)的秩为图G的秩，记为r(G).邻接矩阵A(G)的特征值为图G的特征值.图G的正负惯性指数和零度指其邻接矩阵A(G)所有特征值中正、负和零特征值的个数，分别用p(G),n(G),η(G)表示.正、负惯性指数之差称为符号差，用s(G)表示.若s(G)=0，则称这个图是平衡的.显然，任意二部图是平衡的，但反之不成立.因而一个自然的问题就是刻画所有的平衡图.

记n为一个整数，一个n-圈Cn定义为一个包含n个顶点和n条边的图，其顶点集和边集分别记为V={a1,a2,…,an}，E={e1,e2,…,en}，对于每个i(1≤i≤n)，ei的端点是ai-1和ai.由一个n-圈Cn添加一个新的顶点，并将该顶点与圈的所有n个顶点相连，得到的图称为轮图，记为Wn.

1 相关引理

引理1.1[3]设v是G的任意顶点，则s(G-v)-1≤s(G)≤s(G-v)+1，当且仅当r(G-v)=r(G)或r(G-v)=r(G)-2时，s(G)=s(G-v).

引理1.2[4]令n=4q+r，n≥3，其中，n,r都是正整数，q为非负整数，且3≤r≤6.则

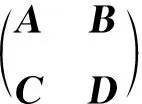
若D为可逆矩阵，则

2 主要结果

记Wn是一个顶点集为V(Wn)={v0,v1,v2,…,vn}，边集为E(Wn)={v0vj|j=1,2,…,n}∪{v1,vn}∪{vjvj+1|j=1,2,…,n-1}的n+1阶的n-轮图.

定理2.1 设Wn是n+1阶的轮图，若n=1(mod4)，则s(Wn)=0，轮图Wn平衡；若n≠1(mod4)，则s(Wn)≠0，轮图Wn不平衡.

证明 首先将n的取值分为下面两种情况：

(i)当n=0(mod2)时，删去度为n的顶点得到圈Cn，根据引理1.1可知，

s(Cn)-1≤s(Wn)≤s(Cn)+1,

(1)

即有

-1≤s(Wn)≤1.

(2)

当n=0(mod4)时，对于邻接矩阵A，存在可逆的n+1阶矩阵P，

使得PAPT=B，计算可得

则矩阵A与矩阵B等价.即当n=0(mod4)时，r(A)=r(B)=n-1，即η(Wn)=2，r(Wn)=n-1.

由等式p(Wn)+n(Wn)=r(Wn)可得，p(Wn)+n(Wn)=n-1.由式(2)可知，n=0(mod4)时，r(Wn)=n-1，s(Wn)≠0.

当n=2(mod4)时，对于邻接矩阵A，也存在可逆的n+1阶矩阵P，

使得PAPT=B，计算可得

即当n=2(mod4)时，r(A)=r(B)=n，η(Wn)=0，r(Wn)=n+1.由等式p(Wn)+n(Wn)=r(Wn)可得，p(Wn)+n(Wn)=n+1.由式(2)可知，当n=2(mod4)时，r(Wn)=n+1，s(Wn)≠0.

(ii)当n=1(mod2)时，将图Wn的邻接矩阵A构造为分块矩阵：

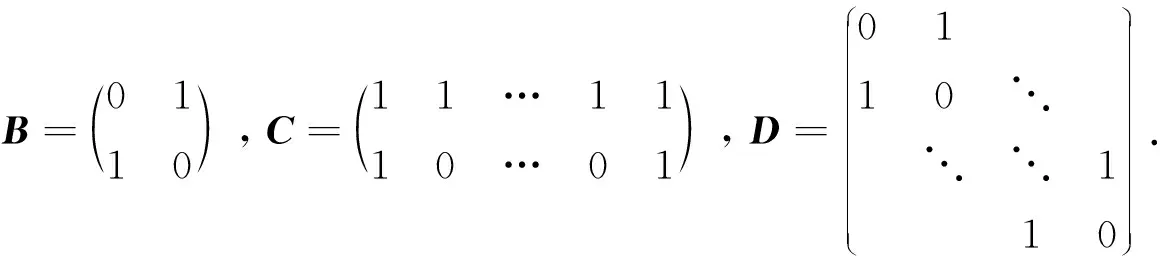
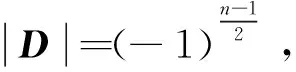
当n=1(mod4)时，矩阵D为n-1阶实对称矩阵，且有

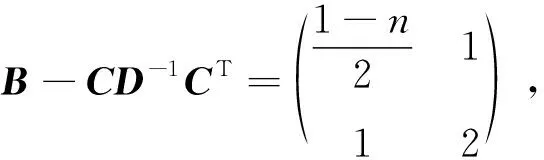
当n=3(mod4)时，矩阵D也为n-1阶实对称矩阵，且有

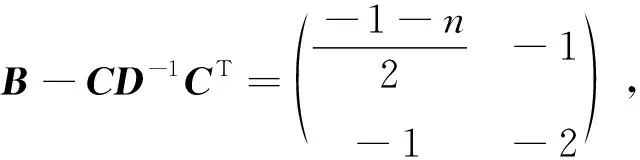
当n=1(mod2)时，删去图Wn中度为n的顶点得到圈Cn，由引理1.2可知，此时r(Cn)=n，即r(Wn)=n+1=r(Cn)+1，则s(Wn)=s(Cn)+1或s(Wn)=s(Cn)-1.而当r(W5)=6=r(C5)+1时，有s(W5)=0≠s(C5)+1.当r(W3)=4=r(C3)+1时，有s(W3)=-2≠s(C3)+1.故s(Wn)=s(Cn)+1不成立，而s(Wn)=s(Cn)-1成立.因此，当n=1(mod4)时，有s(Cn)=1，s(Wn)=s(Cn)-1=0.当n=3(mod4)时，s(Cn)=-1，s(Wn)=s(Cn)-1=-2≠0.

综上所述，当n=1(mod4)时，有s(Wn)=0，则轮图Wn是平衡图；当n≠1(mod4)时，有s(Wn)≠0，则轮图Wn不是平衡图.