Yule-Furry经典δ冲击模型的寿命性质
2024-01-17拉毛措
马 明, 拉毛措, 彭 博, 马 岚, 黄 嫒
(西北民族大学 数学与计算机科学学院, 兰州 730030)
1 引言与预备知识
系统在运行过程中随机受某些外部因素的影响, 如环境温度、 机械参数、 电流等, 这些因素可能导致某些硬件的性能降低从而引起系统故障. 为研究这类系统的可靠性, 本文把这些外部因素视为可能导致系统故障的随机冲击, 通过研究冲击系统的可靠度、 平均寿命、 冲击度等可靠性指标和寿命性质, 预测该系统的寿命, 从而给出相关更换策略, 防止系统突发故障. 因此, 冲击模型在可靠性理论中具有重要意义.δ冲击模型是冲击间隔引起系统失效的冲击模型, 关于δ冲击模型的基础研究目前已有很多结果, 例如: Li等[1]和李泽慧等[2]研究了冲击是按齐次Poisson过程到达的δ冲击模型; 唐风琴等[3]研究了基于时倚Poisson过程的δ冲击模型; Li等[4]将齐次Poisson过程进行一般化, 研究了非齐次Poissonδ冲击模型; Eryilmaz[5]研究了冲击过程为Polya过程的δ冲击模型.关于δ冲击模型的扩展研究目前也有一些成果, 例如: Wang等[6]研究了间隔服从独立同分布的δ冲击模型与极端冲击模型相结合的混合冲击模型; Parvardeh等[7]分别讨论了混合δ冲击模型下模型Ⅰ(当连续两次冲击之间的时间小于阈值δ, 或单个冲击幅度大于阈值γ时, 系统失效)和模型Ⅱ(当连续两次冲击之间的时间小于一个阈值δ, 或累积冲击幅度大于一个固定的阈值γ时, 系统失效)的生存函数和寿命T的Laplace变换; Lorvand等[8]扩展了Parvardeh等[7]的研究, 建立了混合δ冲击模型下具有多状态的系统, 并推导了该系统在完全工作状态下和部分工作状态下的生存函数及相应的前两个矩; Jiang[9]研究了冲击是按照Poisson过程到达的具有多失效阈值的广义δ冲击模型, 分析并推导了平均成本率和平稳可用性, 在可用性约束下, 通过数值计算得到了最优的订货替换策略; Kus等[10]研究了连续冲击之间的到达间隔时间属于一类矩阵指数分布的δ冲击模型的混合δ冲击模型, 得到了系统寿命的Laplace-Stieltjes变换的矩阵形式; Goyal等[11]研究了冲击过程为Poisson广义Gamma过程的δ冲击模型, 推导了生存函数与平均寿命的关系, 并研究了一些相关的随机性质.文献[12-14]给出了相关δ冲击模型的一些新成果.
上述结果都是在冲击间隔服从独立同分布或冲击到达率不变的前提下研究的, 但在实际应用中, 系统遭受的冲击强度并非恒定. 本文将讨论冲击到达率线性变化的Yule-Furry经典δ冲击模型, 建立Yule-Furry经典δ冲击模型, 给出Yule-Furry经典δ冲击模型的系统冲击度及平均冲击度, 给出可靠度的显式表达式及其性质, 并讨论寿命T的矩母函数和Laplace函数, 给出该模型的平均寿命r阶矩, 最后给出该模型的一个实例. 下面给出一些相关定义和引理.
定义1[15]设计数过程{X(t),t≥0}是一个连续时间Markov链, 给定常数λ>0,m=1,2,….若对∀t≥0,h>0,n=m,m+1,…, {X(t),t≥0}满足:
1)X(0)=m;
2)P(X(t+h)-X(t)=1|X(t)=n)=nλh+ο(h);
3)P(X(t+h)-X(t)≥2|X(t)=n)=ο(h).
则称{X(t),t≥0}是一个参数为(m,λ)的Yule-Furry过程, 也称为线性纯生过程, 记作{X(t),t≥0}~YFP(m,λ), 其中λ称为生率系数,mλ称为初始生率.
定义2[16]事件点在时间轴上随机分布的现象称为随机点过程, 简称点过程, 记作Ψ.
给定一个点过程Ψ, 对于∀t>0,n=1,2,…, 用N(t)表示在[0,t)上发生的事件点个数,Sn为第n个事件点发生的时刻,Zn表示第(n-1)个和第n个事件点的时间间隔, 其中Z1表示首次冲击时刻, 则随机过程{N(t),t≥0}, {Sn,n=1,2,…}, {Zn,n=1,2,…}分别称为点过程Ψ的点数过程、 点时过程、 点距过程, 常用点过程的这3种随机过程表征随机点过程Ψ.
定义3[16]设{N(t),t≥0}是点过程Ψ的点数过程, 给定正整数m, 对∀t≥0, 令X(t)=N(t)+m, 如果{X(t),t≥0}~YFP(m,λ), 则称Ψ是一个参数为(m,λ)的Yule-Furry点过程, 记作Ψ~[YFP(m,λ)].
引理1[15]设点过程Ψ~[YFP(m,λ)].{N(t),t≥0}, {Sn,n=1,2,…}, {Zn,n=1,2,…}分别是Ψ的点数过程、 点时过程、 点距过程, 则Ψ有以下性质(其中规定00=1):
1) 对于t≥0, 点数N(t)服从参数为(m,e-λt)的非负值负二项分布, 其分布列为
2) 对于n=1,2,…, 点距Z1,Z2,…,Zn相互独立且Zn服从参数为(n+m-1)λ的指数分布, 即Zn的生存函数为
3) 若m=1, 则对于n=1,2,…, 点时Sn的分布函数为
定义4[17]对于非负随机变量X和Y, 若∀t≥0, 有
P(X>t)≥P(Y>t),
则称X随机地大于Y, 记作X≥stY.
引理2[17]若X≥stY, 则EX≥EY.
2 Yule-Furry经典δ冲击模型
考虑一个在连续时间尺度上运行的系统, 该系统遭受外部随机冲击, 假设冲击按一个参数为(m,λ)的Yule-Furry点过程到达, 如果相邻两次冲击间隔小于给定的正实数δ, 则系统失效(假设首次冲击时刻小于δ, 系统也失效), 这样的模型称为Yule-Furry经典δ冲击模型.该模型定义如下:
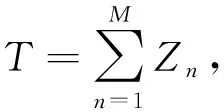

3 冲击度
首先讨论点距Zi(i=1,2,…)与系统失效前总冲击次数M之间的关系.M的分布列通常称为冲击度.
定理1在SM{YFP(1,λ),D(δ)}中, 系统的冲击度和平均冲击度分别为
P(M=n)=(1-e-nλδ)e-n(n-1)λδ/2,n=1,2,…
和
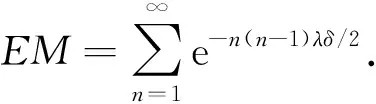
(1)
证明: 首先根据定义5, 可得
P(M=1)=P(Z1<δ)=1-e-λδ.
当n≥2时, 由于
P(M>n)=P(Z1≥δ,Z2≥δ,…,Zn≥δ)=e-n(n+1)λδ/2,
(2)
P(M>n-1)=P(Z1≥δ,Z2≥δ,…,Zn-1≥δ)=e-n(n-1)λδ/2,
(3)
因此由式(2)和式(3)得
P(M=n)=P(M>n-1)-P(M>n)=e-n(n-1)λδ/2-e-n(n+1)λδ/2=(1-e-nλδ)e-n(n-1)λδ/2.
(4)

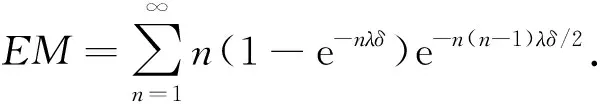
(5)
事实上, 一方面, 由于
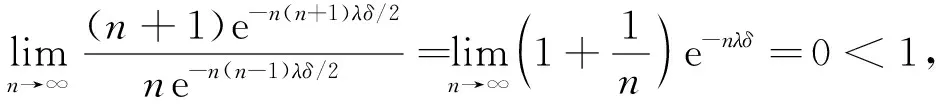
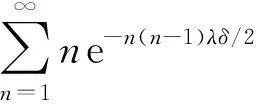
在式(6)中, 由于
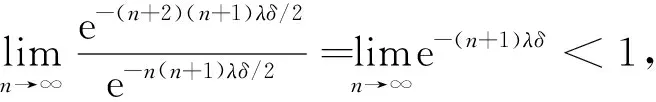

一般将式(2)中的P(M>n)称为系统的累积冲击度.
4 可靠度
下面给出SM{[YFP(1,λ)],D(δ)}系统可靠度的精确表达式.
定理2设T~SM{[YFP(1,λ)],D(δ)}, 则系统可靠度为
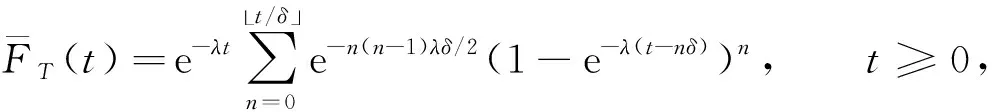
(7)

证明: 对于∀t≥0, 有
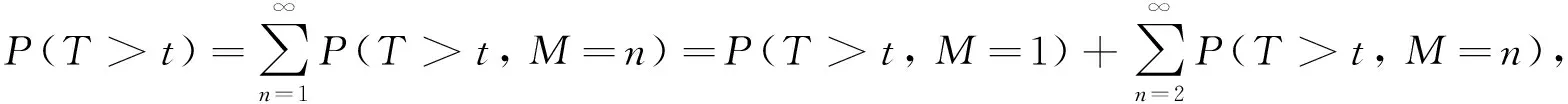
(8)
其中{M=1}表示首次冲击导致系统失效, 即T=Z1≤δ, 则
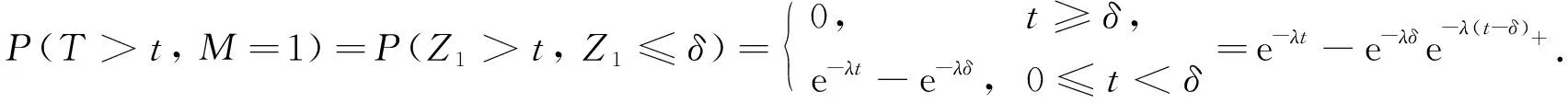
(9)
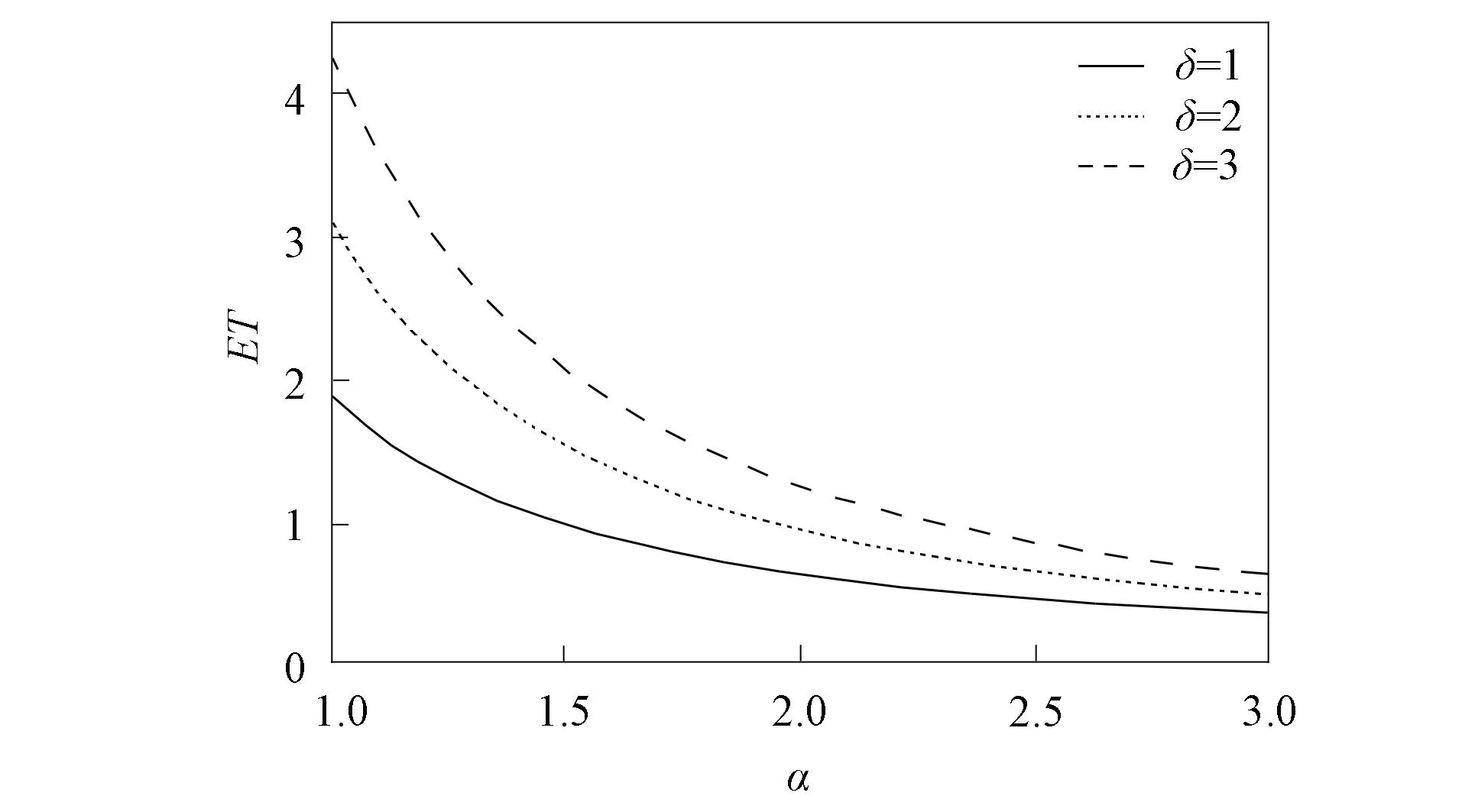
下面考虑n≥2的情形.由于{M=n}={n-1 由于点距Zi(i=1,2,…,n)服从参数为iλ的指数分布, 因此由指数分布无记忆性得 P(Sn>t|M>n-1)=P(Sn>t|Z1≥δ,Z2≥δ,…,Zn-1≥δ)=P(Sn>(t-(n-1)δ)), 根据引理1中3)可得 即 P(Sn>t|M>n-1)=1-(1-e-λ(t-(n-1)δ)+)n. (11) 同理 P(Sn>t|M>n)=P(Sn>t-nδ)=1-(1-e-λ(t-nδ)+)n. (12) 将式(11),(3),(12),(2)依次代入式(10), 得 P(T>t,M=n)=e-n(n-1)λδ/2[1-e-nλδ-(1-e-λ(t-(n-1)δ)+)n+e-nλδ(1-e-λ(t-nδ)+)n]. (13) 式(13)包含了式(9), 即n=1的情形.把式(13)代入式(8)得 (14) 由定理1注意到 e-n(n-1)λδ/2(1-e-nλδ)=P(M=n), 且 (15) 所以 当n=0时, e-n(n+1)λδ/2(1-e-λ(t-nδ)+)n=1, 于是, 式(16)可写为 (17) 对式(17)中的第二项变量替换再合并, 即 由于当t≥0时, 对∀n=1,2,…, 有 因此 证毕. 根据定理2易得如下推论. 推论1若对于0<δ1<δ2,Tδ1~SM{[YFP(1,λ)],D(δ1)},Tδ2~SM{[YFP(1,λ)],D(δ2)}, 则有Tδ1≥stTδ2. 证明: 由式(7)知, 对于∀t≥0, 有 由于0<δ1<δ2, 故有以下关系: e-n(n-1)λδ1/2≥e-n(n-1)λδ2/2>0, (1-e-λ(t-nδ1))n≥(1-e-λ(t-nδ2))n>0, 其中n=0时等号成立.从而 于是对于∀t≥0有 故 P(Tδ1>t)≥P(Tδ2>t). 由定义4知,Tδ1随机地大于Tδ2.证毕. 推论2对于t≥0,n=0,1,…, SM{[YFP(1,λ)],D(δ)}系统的存活概率为 证明: 由于{T>t,N(t)=n}⟺{N(t)=n,M>n}, 因此 由定义5及引理1中1)得 P(N(t)=0,M>0)=P(N(t)=0)=e-λt, 则 (18) 当n=1,2,…时, 由于{N(t)=n,M>n}⟺{Sn≤t P(N(t)=n,M>n)=P(Sn≤t (19) 由于点距Zi(i=1,2,…,n)服从参数为iλ的指数分布, 因此由指数分布无记忆性及引理1中1)得 将式(20)和式(2)代入式(19)可得 P(N(t)=n,M>n)=e-n(n+1)λδ/2e-λ(t-nδ)+(1-e-λ(t-nδ)+)n, (21) 从而对于n=1,2,…, ∀t≥0, 由式(21)和引理1中1)得 易见, 式(22)包含了式(18)即n=0的情形, 所以式(22)对n=0,1,…都满足.证毕. 下面给出SM{[YFP(1,λ)],D(δ)}系统寿命T的矩母函数. 定理3设T~SM{[YFP(1,λ)],D(δ)}, 则寿命T的矩母函数为 (23) 且在任意区间(-∞,a]上是一致收敛的, 其中0 证明: 由定义5可得 (24) 由于点距Zk(k=1,2,…)服从参数为kλ的指数分布, 因此当n=1时, (25) 当n>1时, (26) 由指数分布的无记忆性得 (27) (28) 将式(27),(28)代入式(26)得 (29) 式(29)包含了式(25)即n=1的情形, 将式(29),(4)代入式(24)可得式(23). e-(nλ-2t)(n-1)δ/2≤e-λ(n-2)(n-1)δ/2, 1-e-δ(nλ-t)<1. 而对∀n≥2, 有 所以 由于寿命T的Laplace变换LT(t)和矩母函数φT(t)有以下关系: LT(t)=φT(-t), 所以由定理3易得如下推论. 推论3寿命T的Laplace函数为 (30) 其中0 定理3表明, 矩母函数φT(t)的级数形式在(-∞,a]上一致收敛, 由于矩母函数的存在域(-∞,a]包含0, 所以φT(t)在该存在域内的各阶导数存在, 且T的各阶矩都存在. 定理4设T~SM{[YFP(1,λ)],D(δ)}, 则系统失效前平均寿命为 (31) 下面用3种方法证明式(31)成立. (32) 设A>0, 式(32)等号右边可写成 (33) 0 (34) ln|f(x)|=xln(1-e-λ(t-xδ)), (35) 对式(35)两边求导可得 下面讨论函数g(t)≜e-λte-n(n-1)λδ/2(1-e-λ(t-nδ)+)n在[0,A]上的连续性.对于 首先, 在t∈(-∞,nδ)和t∈(nδ,∞)内,g(t)各段都是由初等函数构成的, 所以在各自区间内g(t)连续; 然后, 考虑点t=nδ处的连续性, 对于∀n≥1, 由于 即g(t)在点t=nδ处连续, 因此g(t)在t∈(-∞,∞)上连续. (36) 对于n=0,1,…, 有 (37) 将式(37)代入式(36), 再代入式(33),(32)得 (38) 将其代入式(38)得 2) 取条件法.由双期望公式得 易知 (40) 当n>1时, 给定条件Zi≥δ(i=1,2,…,n-1)下点距Zi的条件期望为 则 于是 (41) 将式(41),(40),(4)代入式(39)得 由式(5)和式(1)易知, 则 (43) 则式(43)等价于 (44) (在式(44)等号右边级数也收敛的条件下).再由式(3),(4)易知 (45) 从而由式(43)~(45)易得 3) 矩母函数法.对式(23)表示的矩母函数φT(t)关于t逐项求导, 可得 则 由于φT(t)的存在域包含0, 所以φT(t)在0点处可导, 于是 这与式(42)等价.证毕. 由推论1和引理2易得平均寿命关于失效参数的单调性. 推论4设T~SM{[YFP(1,λ)],D(δ)}, 则ET关于δ单调递减. 实际上, 设0<δ1<δ2, 则对∀k=1,2,…, 有 其中k=1时等号成立.因此, 由定理4也可立得推论4. 下面讨论寿命T的任意阶矩. 推论5设T~SM{[YFP(1,λ)],D(δ)}, 则寿命T的r阶矩为 (46) |tr-1e-[n(n-1)δ+2t]λ/2|≤Ar-1e-n(n-1)δλ/2, (47) (48) 所以 将式(50)代入式(49)得 所以 又由于 证毕. 易知, 当r=1时, 式(46)可约简为 (51) 式(51)与式(31)一致. 本文结合SM{[YFP(1,λ)],D(δ)}模型的构造, 给出了该模型系统的可靠度、 冲击度、 平均寿命等可靠性指标. 下面给出该模型的一个应用实例. 癌症是一种常见的慢性病, 一般由内源因素导致基因损伤, 使早期癌细胞生长并侵害正常细胞, 最终导致癌症. Chen等[19]发现了另一种引发癌症细胞的细胞机制——细胞分裂速度, 即细胞增殖速度过快会导致细胞癌变. 假设细胞增殖按Yule-Furry过程进行分裂,Sn为细胞第n次分裂的时刻,Zn表示细胞第(n-1)次与第n次分裂的时间间隔, 常数δ为正常细胞分裂周期所需的最小时间.当首次存在某个n, 使得Zn<δ(即该细胞分裂的第n个时间间隔小于δ)时细胞癌变.在细胞分裂过程中有许多酶参与, 而内部因素会影响酶活性, 酶活性越强, 细胞分裂速度越快.假设酶的活性为α(α>0), 则细胞分裂速率λ=f(α), 其中f(α)是单调递增函数, 设T表示直到癌变为止细胞的寿命, 则细胞寿命T服从一个Yule-Furry经典δ冲击模型, 由定理4知该细胞的平均寿命ET为 下面数值模拟f(α)=α时细胞的平均寿命.本文对酶的活性α和时间δ取几个特殊值观察平均寿命ET的变化情况, 结果分别如图1和表1所示.由图1和表1可见,ET关于参数α和δ都单调递减.说明细胞分裂中参与的酶活性越强, 细胞分裂周期所需的时间越长, 细胞分裂速度越快, 越容易癌变. 表1 参数α和δ取特殊值时ET的值 图1 ET关于参数α和δ的变化趋势Fig.1 Changing trend of ET with parameters α and δ 下面对Poisson经典δ冲击模型(SM{[HPP(0,λ)],D(δ)})与Yule-Furry经典δ冲击模型的寿命性质进行比较, 结果列于表2. 由表2可见, 这两类模型的平均寿命都关于失效参数δ单调递减, Poisson经典δ冲击模型的存活概率与冲击到达率λ无关, 而Yule-Furry经典δ冲击模型中, 冲击到达率是线性变化的, 所以其寿命指标均与冲击到达率有关. 表2 Poisson经典δ冲击模型与Yule-Furry经典δ冲击模型的寿命指标 综上所述, 本文研究了冲击参数为(1,λ)的Yule-Furry经典δ冲击模型, 分别用取条件法、 概率法、 矩母函数法给出了系统可靠度、 平均寿命和矩母函数的显式表达式, 验证了可靠度和平均寿命关于失效参数δ单调递减的性质, 并证明了寿命的任意矩均存在且可以用级数形式显式表示. 最后, 将该模型的平均寿命应用于癌细胞的病例研究中, 发现酶的活性与细胞的平均寿命成反比关系, 即细胞分裂过程中参与酶的活性越强, 细胞的平均寿命越短, 导致该细胞癌变.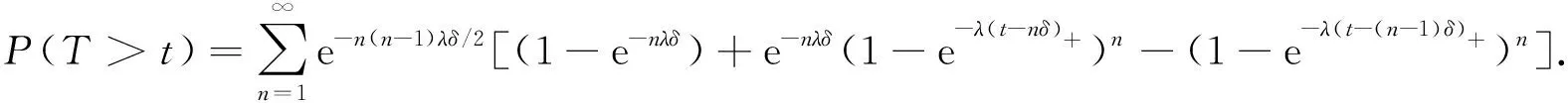

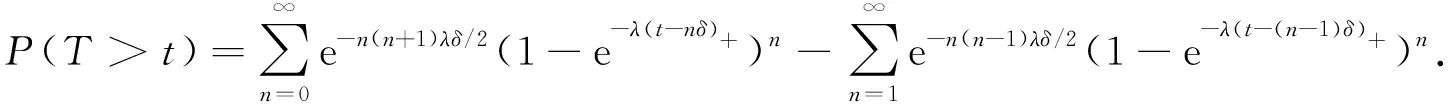

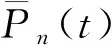
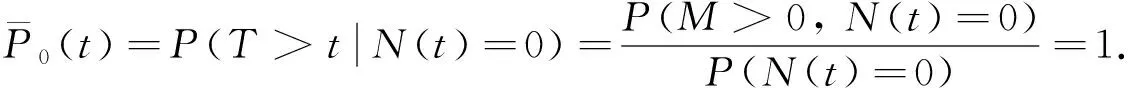
5 矩母函数
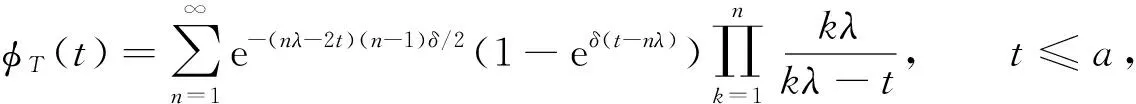
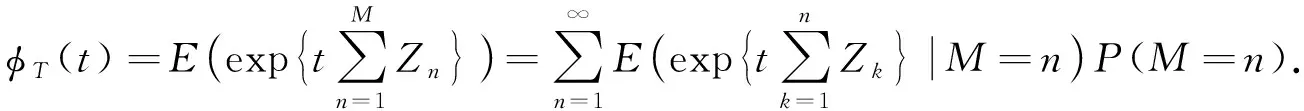

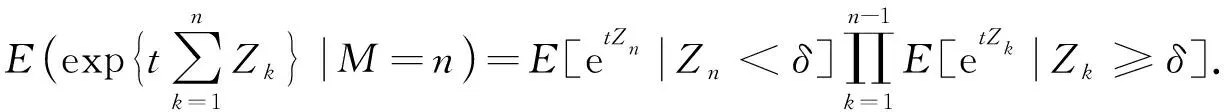
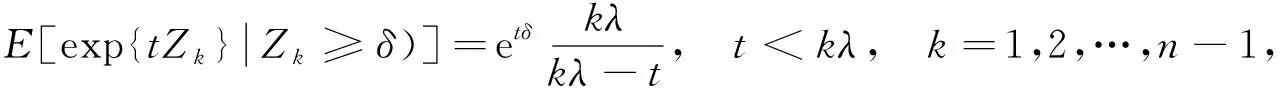
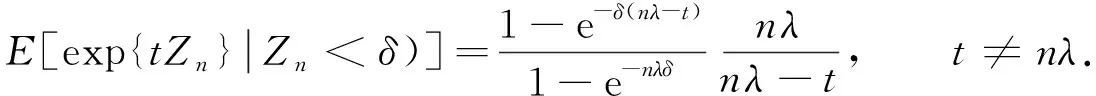

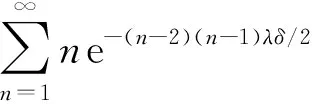

6 寿命的矩
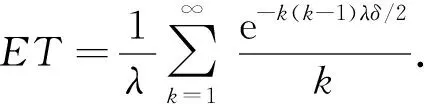

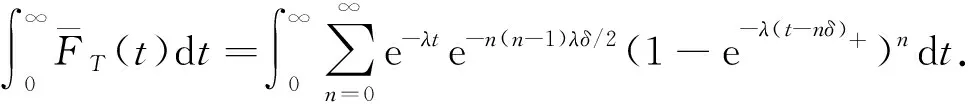
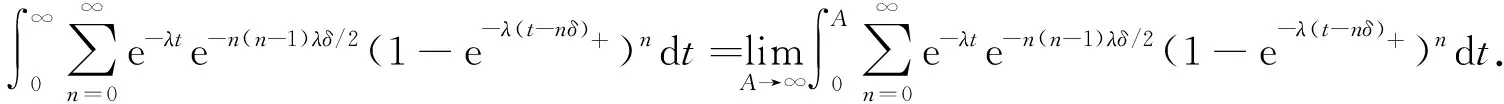

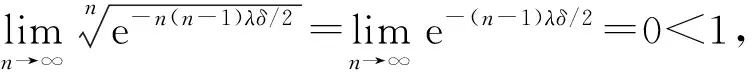



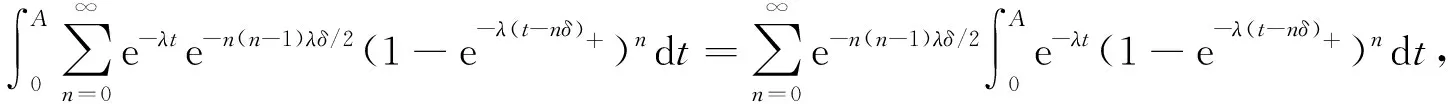




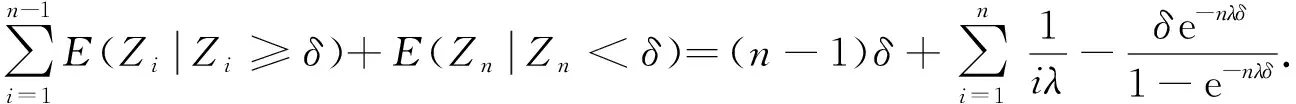
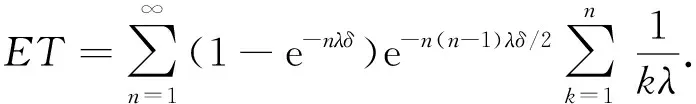

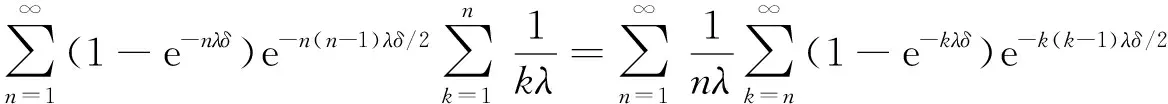




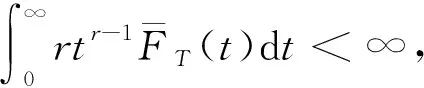
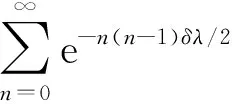




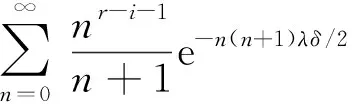
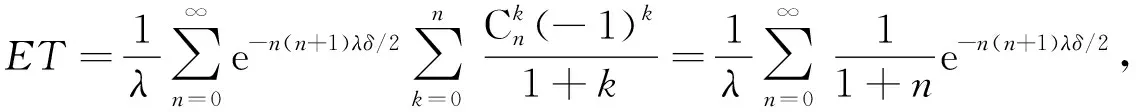
7 实 例