阻尼系统的特征

田红亮 郑金华 方子帆 朱大林

（三峡大学 机械与动力学院，湖北 宜昌 443002）

将式（4）代入式（7）得

1 有阻尼多自由度系统对激励的响应

冲量为U（量纲是N·s）的脉冲力［1］为

物体动量的增量等于它所受合外力的冲量

将式（4）代入式（7）得

当t＞0＋时，脉冲力作用已结束，故t＞0＋时得

将式（11）和式（12）代入式（9）得

将式（15）代入式（13）得

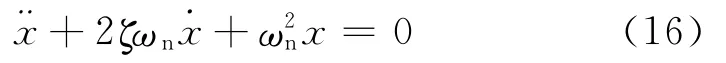
二阶常系数齐次微分方程（16）的特征方程［2］为

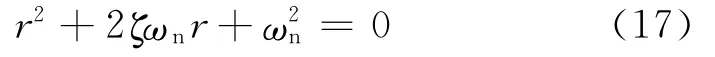
特征方程（17）的两个根为

方程（16）的通解［2］为

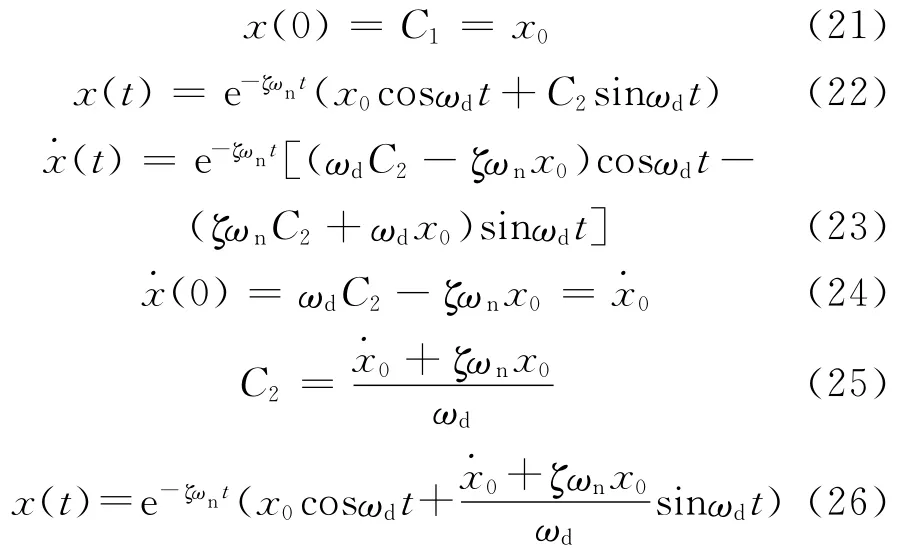
P（t）在t＝τ的冲量为U＝P（τ）dτ，脉冲响应为

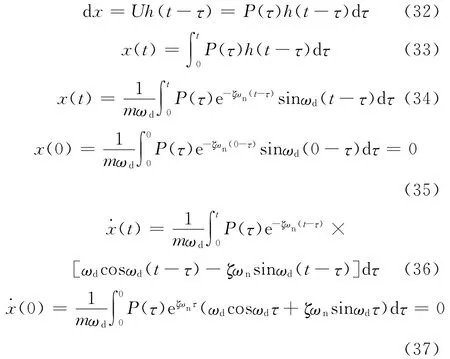
＋＋kx＝P（t）在x0及下的响应为

若y＝y1（x）＋iy2（x）是微分方程y″＋py′＋qy＝f1（x）＋if2（x）的解，则y1（x）与y2（x）分别是微分方程y″＋py′＋qy＝f1（x）与y″＋py′＋qy＝f2（x）的解，其中y1（x）、y2（x）、f1（x）、f2（x）都是x的实函数.

由式（18）可得方程（41）特征方程的根r1，2＝－ζωn±iωd，故iω不是根.方程（41）具有形如以下特解［2］

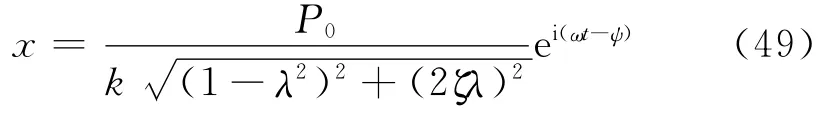
则方程（40）的特解为

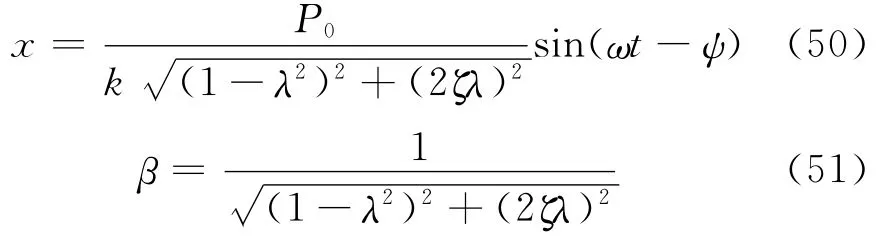
根据式（20）和式（53）可得方程（40）的通解为

将式（60）代入式（57）可得方程（40）的通解为

将式（51）代入式（50）可得方程（40）的稳态响应

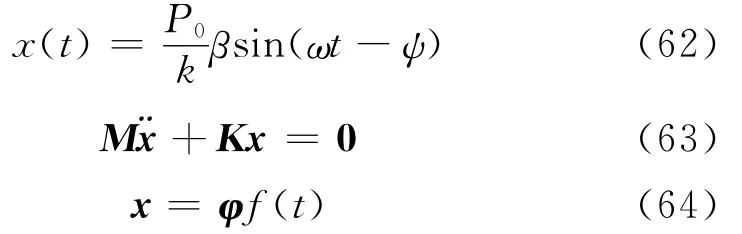
式中，φ＝［φe1φe2…φen］T为特征向量.

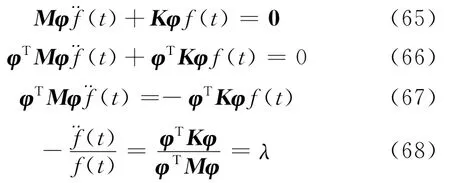
只有当系统中存在无惯性自由度时，才会出现半正定的情况［3］.假设K为半正定实对称矩阵，φTKφ≥0，M为正定实对称矩阵［4］，φTMφ＞0.λ是非负数.

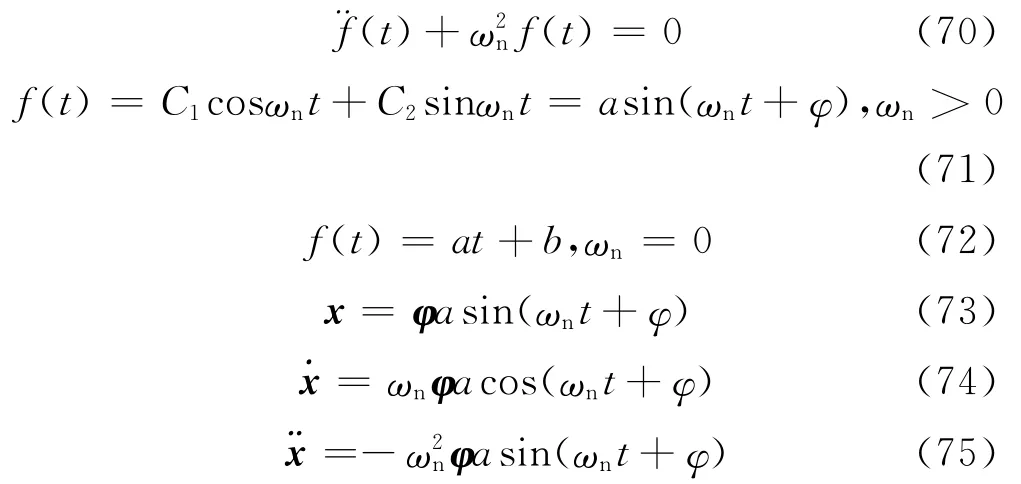
将式（75）和式（73）代入式（63）得

方程（76）存在非零解（至少2组解）φ的条件是［5］

根据式（76）可得第i个特征向量φi满足

当是特征多项式的单根时，式（80）的n个方程中有一个且只有一个是不独立的，不妨设最后一个方程不独立，将它划去，且将含有φi的某个元素（例如φen）的项全部移到等号右端，得

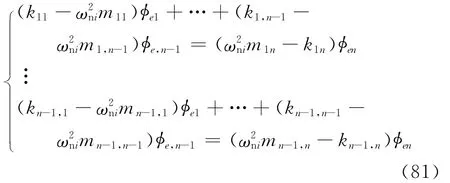
式（81）不同于文献［1］.若方程组（81）左端的系数行列式不是零，则此方程组有且仅有唯一组解［5］，可以解出用φen表示的φe1，φe2，…，φe，n－1；否则应将含φi的另一个元素（如φe，n－1）的项移到等号右端再解方程组.使计算简单，让φen＝1，第i阶主振型为

根据式（73）可得第i阶主振动为

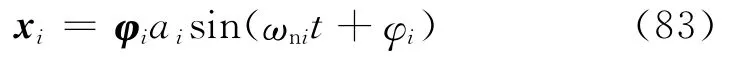
故方程（63）的通解［2］为

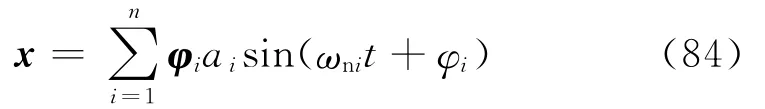
由式（76）得

若i≠j时，ωni≠ωnj，由式（94）得

当j＝i，式（95）和式（96）分别为2个实二次型

将式（95）和式（97）代入式（102）得

将式（96）和式（98）代入式（104）得

由式（86）得

将式（101）代入式（106）得

将式（100）代入式（119）得

根据式（103）和式（113）得

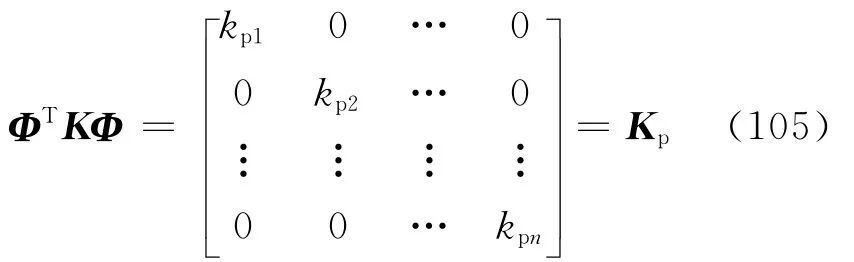
根据式（105）、（120）和式（108）得

式（84）可改写为

将式（95）和式（97）代入式（125）得

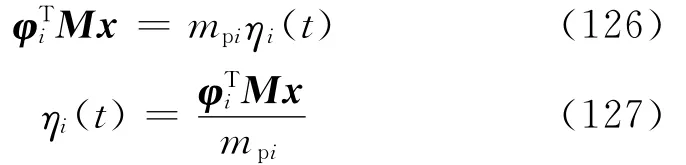
将式（101）代入式（124）得

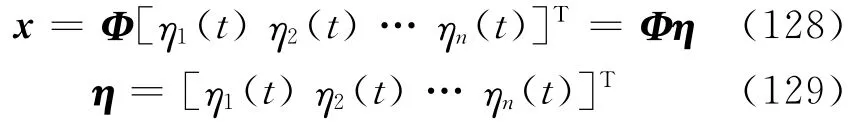
将式（128）代入式（63）得

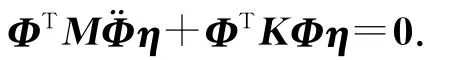
用正则振型矩阵作坐标变换矩阵，式（128）成为

将式（133）代入式（63）得

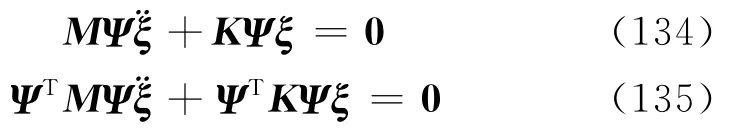
将式（122）和式（123）代入式（135）得

将式（15）代入式（11）得

由式（62）可得方程（151）的稳态响应为

将式（152）代入式（124）得

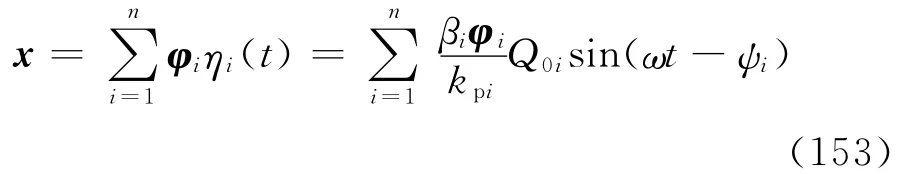
将式（101）代入式（144）并考虑简谐激振力得

2 传递函数与复频响应函数

初始条件为零［6］，对式（139）作Laplace变换

根据式（157）得

式（162）不同于文献［1］中的式（4.227）G（s）＝

将式（101）、（103）、（145）和式（105）代入式（164）得

将式（161）中的s用iω取代后，可得频率特性［7］

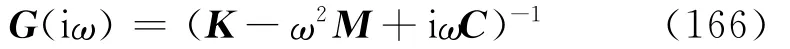
对式（139）两边作Fourier变换［6］得

式（148）除以式（100）得

将φi＝［φ1iφ2i…φri…φni］T和＝［φ1iφ2i…φsi…φni］代入式（177）可得H（ω）的第r行第s列元素［5］

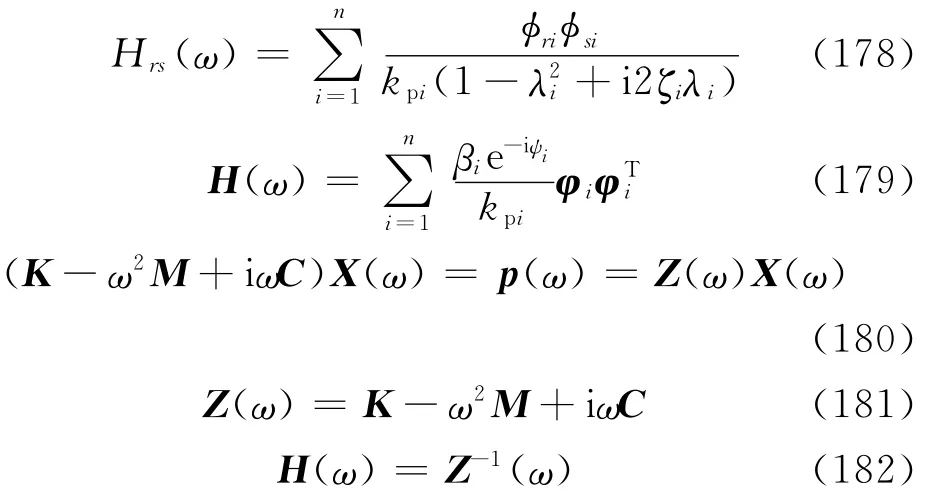
由式（42）与式（47）可得单自由度的复频响应函数

当k＝1N／m，图1示出单自由度复频响应函数.

图1 单自由度系统的复频响应函数

3 工程实例与结果分析

3.1 固有频率相差较大时的情况

图2中m＝1kg，其单位符号kg不同于文献［8］中的 Kg，k＝987N／m，k′＝217N／m，c＝0.628 4N·s／m，c′＝0.062 8N·s／m，P1（t）＝P01sinωt.

图2 有阻尼两自由度系统

代入式（76）得

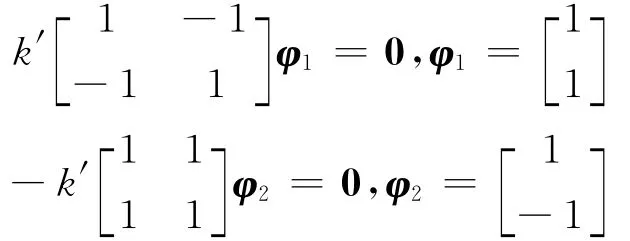
＝987（rad／s）2，ωn1＝31.42rad／s，fn1＝＝6Hz.fn2比fn1大20%.由式（108）和式（101）得

由式（103）和式（143）得

由式（110）和式（148）得

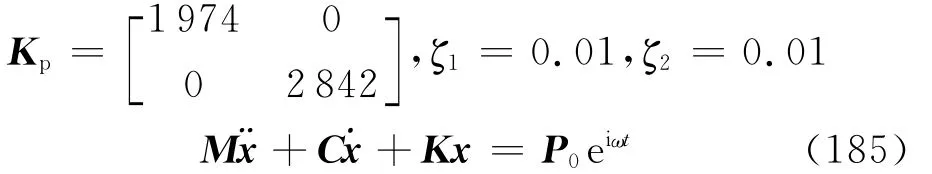
设方程（185）具有形如以下特解

将式（179）代入式（187）得

将式（188）代入式（186）得

故方程（184）的特解为

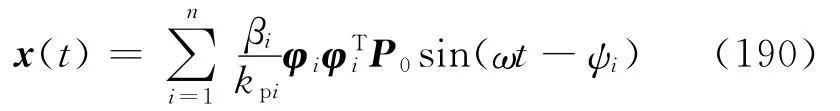
式（190）与式（156）相同.将式（187）展开得

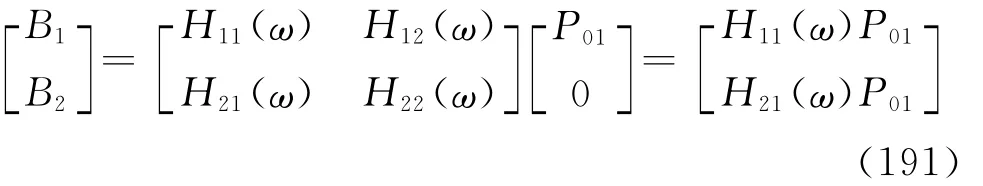
由式（178）得

图3示出有阻尼二自由度系统复频响应函数.

图3 固有频率相差大时二自由度系统的复频响应函数

3.2 固有频率差距较小时的情形

将第3.1节中的两个参数改变为：k′＝10N／m，c′＝0.003 1N·s／m，其它参数不变.

ω2n1＝987（rad／s）2，ωn1＝31.42rad／s，fn1＝5Hz，ω2n2＝100 7（rad／s）2，ωn2＝31.73rad／s，fn2＝5.05Hz.fn2比fn1仅大1%，相当接近.由式（108）和式（101）得

由式（103）和式（143）得

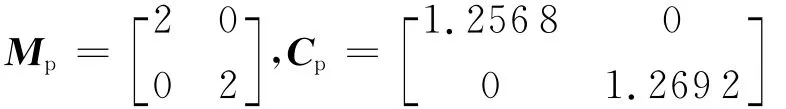
由式（110）和式（148）得

由式（178）得

式（192）不同于文献［1］的下面具体数据

图4示出有阻尼二自由度系统复频响应函数.

图4 固有频率偏差小时二自由度系统的复频响应函数

［1］ 倪振华.振动力学［M］.西安：西安交通大学出版社，1988：61，82，185，203，243－253.

［2］ 同济大学数学系.高等数学（上册）［M］.6版.北京：高等教育出版社，2011：325－326，332－335，341－342.

［3］ 程耀东，李培玉.机械振动学（线性系统）［M］.修订版.杭州：浙江大学出版社，2006：99－107，159.

［4］ 诸德超，邢誉峰.工程振动基础［M］.北京：北京航空航天大学出版社，2005：67.

［5］ 姚慕生，高汝熹.高等数学（二）第一分册线性代数［M］.2版.武汉：武汉大学出版社，2000：46，53，59－60.

［6］ 张元林.工程数学积分变换［M］.4版.北京：高等教育出版社，2004：34，81－82.

［7］ 杨叔子，杨克冲，吴 波，等.机械工程控制基础［M］.5版.武汉：华中科技大学出版社，2006：120.

［8］ 毛宽民，陈天宁，黄协清.外力冲击二级隔离系统参数设计 DEM 研究［J］.应用力学学报，2000，17（2）：100－104.