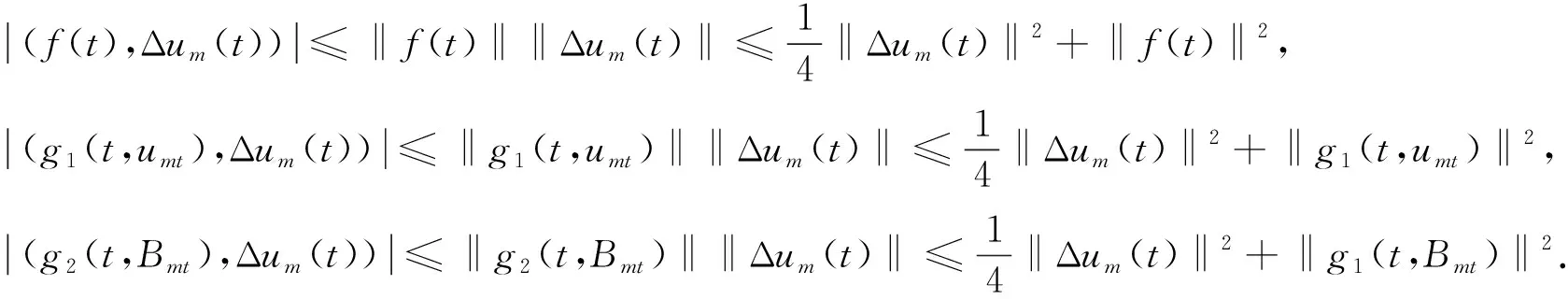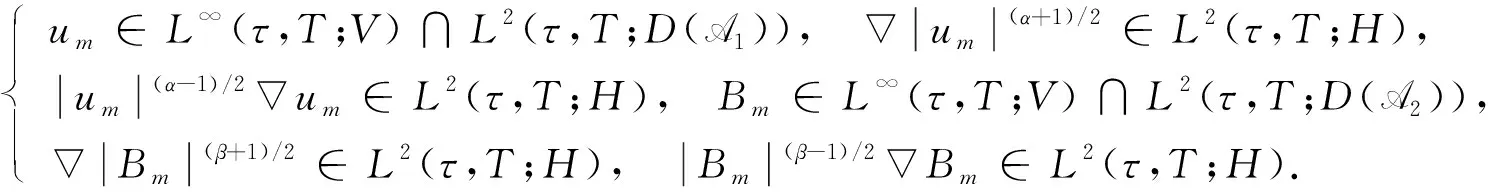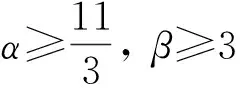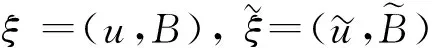带阻尼项和时滞项的三维磁流体方程解的适定性

张明娇, 宋小亚, 李晓军

(河海大学 数学学院, 南京 211100)

磁流体方程是流体力学中Navier-Stokes方程和电动力系统中Maxwell方程的耦合. 磁流体动力学在等离子体物理、 天体物理及控热核聚变和工业新技术中应用广泛. 文献[1-2]研究有界区域上磁流体方程的适定性, 证明了二维磁流体方程弱解和全局强解的存在唯一性, 并得到了三维磁流体方程局部强解的存在唯一性、 弱解的存在性和全局强解的唯一性.

三维不可压磁流体方程弱解的唯一性和强解的全局存在性目前尚未得到证明. 因此, 带阻尼项的三维磁流体方程受到研究者的广泛关注, 并从不同角度进行了研究. 阻尼项主要用于描述各种物理现象, 如阻力、 摩擦效应、 多孔介质流动和一些耗散机制等[3-4]. 关于带阻尼项的三维磁流体方程的研究已取得了丰富成果, 例如, 在满足下列条件之一时:

1)α≥4,β≥4;

文献[5]证明了带阻尼项的三维磁流体方程强解的适定性; 文献[6-7]研究表明, 临界指数3至关重要, 文献[6]对上述条件进行了优化, 在满足下列条件之一时:

4)α≥4,β≥1.

得到了带阻尼项的三维磁流体方程强解的适定性.上述结果表明, 带阻尼项的三维磁流体方程强解适定性的临界指数是α≥3, 而不是α>3.

为更真实描述物理学与生物学等领域内的自然现象, 关于三维磁流体方程本文引入了时滞项.时滞效应主要用于描述物理和生物等领域内的时间延迟效应, 时滞效应的影响通常体现为: 当想通过施加外力控制系统时不仅要考虑到系统的当前状态而且还要考虑系统的历史状态.与不带时滞项的三维磁流体方程相比, 该模型中g1(t,ut),g2(t,Bt)的非自治固有性会导致一些困难, 尤其是紧性方面的困难.例如: 文献[8]证明了带时滞项的二维磁流体方程强解的适定性; 当B=0时带时滞项的磁流体方程简化为带时滞项的Navier-Stokes方程, 文献[9]研究了带时滞项的二维Navier-Stokes方程强解的适定性. 基于此, 本文主要考虑带阻尼项与时滞项的三维磁流体方程, 证明其解的存在性和唯一性, 同时确定阻尼项中的最优指数. 所以本文的研究结果不仅丰富了无穷维动力系统的内容, 而且在流体动力学模型后续的研究中具有促进作用.

1 预备知识

考虑有界域上具有非线性阻尼和时滞项的三维磁流体方程:

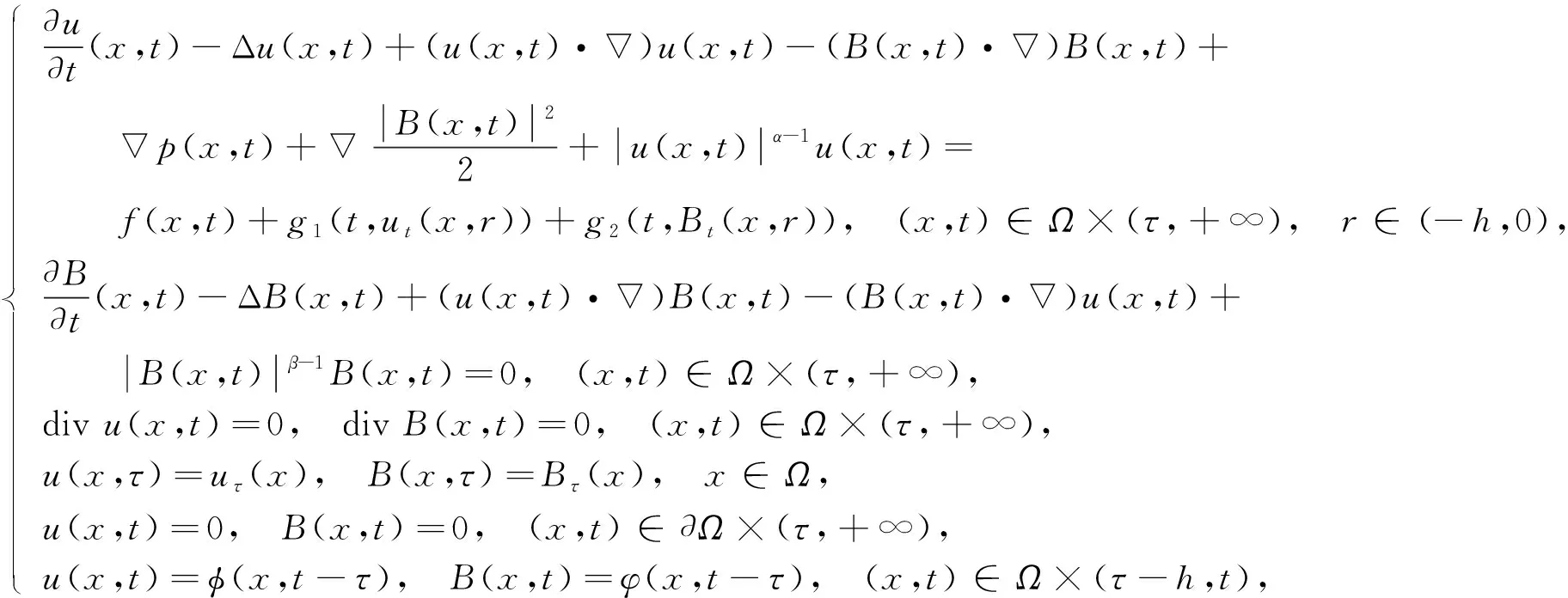
(1)

其中Ω⊂3为有界开集,α≥1,β≥1为正常数,u(x,t),B(x,t)分别表示速度场和磁场,p(x,t)表示压力场,f(x,t)表示外力,g1(t,ut),g2(t,Bt)表示时滞项.

令1≤p≤∞, 下面引入一些函数空间和算子:

通过考虑通常的抽象空间, 可将系统(1)进行简化, 令

定义H,V空间上的内积如下:

并且

V=V×V, H=H×H,V*是V的对偶空间.

则有V⊂H=H*⊂V*, 并且其中的映射是连续且稠密的.

下面定义3个算子A1,A2∈L(V,V*),A∈L(V,V*):

可将A1,A2,A视为(H,H,H)上的无界算子, 定义域为

D(A1)={u∈V,A1u∈H},D(A2)={B∈V,A2B∈H},D(A)=D(A1)×D(A2).

由文献[1]可得

D(A1)=H2(Ω)∩V,D(A2)=H2(Ω)∩V,D(A)=H2(Ω)∩V.

下面引入三线性形b:

可知三线性形b在空间(H1(Ω))3上是连续的, 且有

b(u,v,v)=0, ∀u∈V, ∀v∈H1(Ω),

b(u,v,w)=-b(u,w,v), ∀u∈V, ∀v,w∈H1(Ω).

引理1[10]对任意的u=(u1,u2,u3)∈3, 记F(u)=u, 则F(u)在3中连续可微, 并且

则F(u)是正定的, 且有

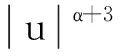
其中正常数c仅依赖于Ω.

引理2[10]以下事实成立:

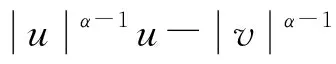
下面对时滞项进行适当的假设[9,11].设(X,Y)是Banach空间,g:×CX→Y且下列条件成立:

(i) 对所有的u∈CX, 映射t∈→g(t,u)∈Y是可测的;

(ii) 对于每个t∈,g(t,0)=0;

(iii) 存在Lg>0, 使得∀t∈及∀u,v∈CX, 有

‖g(t,u)-g(t,v)‖Y≤Lg‖u-v‖CX.

(iv) 存在θ0≥0,Cg>0, 使得对∀θ∈[0,θ0], ∀τ∈t及∀u,v∈C0([τ-h,t];X), 有

下面针对时滞项引入一些空间:

其对应的范数分别为

2 强解的存在性及唯一性

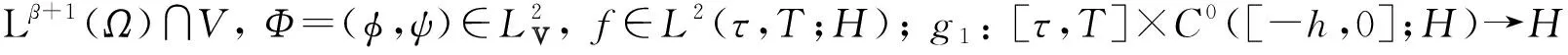
4)α≥7,β≥3.

则有

ξ=(u,B)是系统(1)的强解且唯一.

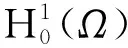
对每个固定的正整数m, 设

(2)

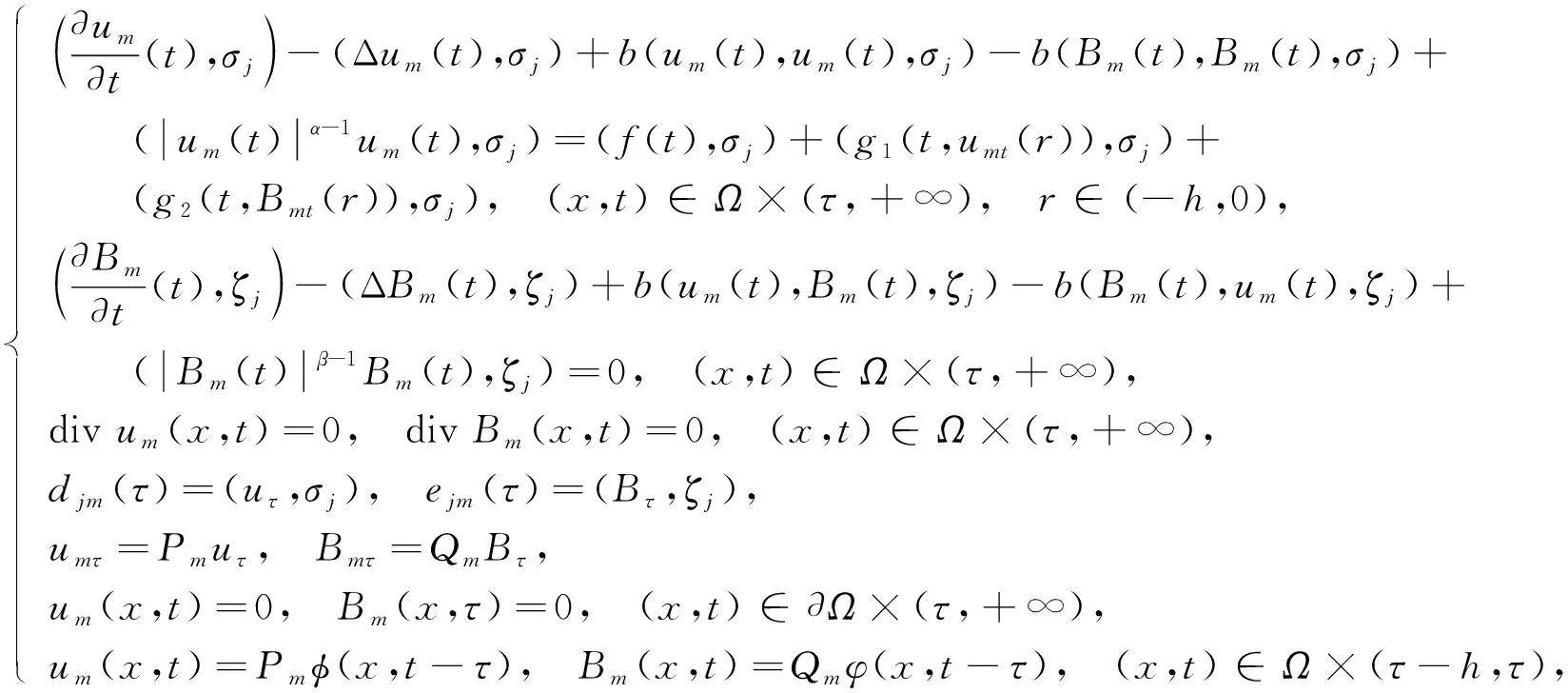
(3)

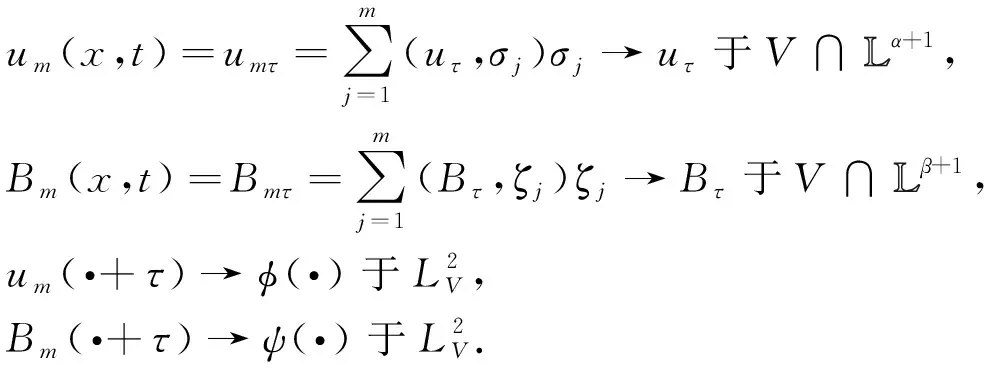
(4)

由常微分方程解的存在性和唯一性性质可知, 对每个整数m=1,2,…, 均存在式(2)满足式(3)定义在区间[τ,Tm](τ

下面给出解ξm(x,t)=(um(x,t),Bm(x,t))的一些先验估计.

1) 对式(3)中第一式和第二式分别乘djm(τ),ejm(τ), 再对j=1,2,…,m进行求和, 得

由于

b(um(t),um(t),um(t))=0,b(um(t),Bm(t),Bm(t))=0,

b(Bm(t),Bm(t),um(t))=-b(Bm(t),um(t),Bm(t)),

因此通过Hölder不等式、 Young不等式、 Poincaré不等式, 可得

在先秦儒家的叙事里，男女之别往往等同于内外、公私与主从之别，主要体现于以下方面：一是生活空间上的隔离，二是社会活动领域上的区分，三是社会角色与道德教化上主从关系的确立。

进一步可得

‖um(t)‖2+‖Bm(t)‖2≤K1, ∀t∈[τ,T].

(7)

利用式(4),(6),(7)可推出

综上可得

(8)

2) 对式(3)中第一式和第二式分别乘δjdjm(t),κjejm(t), 再对j=1,2,…,m进行求和, 得

其中

进一步, 有

由Hölder不等式和Young不等式, 可得

(10)

下面分两种情形讨论.

情形① 由Young不等式和引理2, 可得

下面对其他项进行估计:

结合式(12)及Hölder不等式, 可得

由Gagliardo-Nirenberg不等式和Sobolev嵌入定理, 得

再由上述估计及Young不等式, 可得

将式(10),(11),(13)代入式(9), 可得

(15)

情形②

由Hölder不等式, 可得

由Gagliardo-Nirenberg不等式, 可得

‖um(t)‖L2(α+1)/(α-1)≤C‖um(t)‖(α-2)/(α+1)‖2um(t)‖3/(α+1),α≥2.

由上述估计及Young不等式, 可得

将式(10),(16)代入式(9), 可得

综上可知, 当α≥3, 4≤β≤5或α≥4,β≥1时, 有式(15).

由Young不等式, 可得

由上述结果可得

对式(18)中t在区间[τ,t]上进行积分, 可得

(19)

4) 由式(15),(19)以及文献[12]中的一些插值结果, 得

ξm∈C0([τ,T];V).

(20)

5) 由式(4),(15),(19),(20)可知, 可找到序列ξm的子列ξmk(其中ξmk={umk,Bmk}), 具有以下性质:

①ξmk在空间L2(τ,T;D(A))中弱收敛到ξ;

②umk在空间L∞(τ,T;V)∩L∞(τ,T;Lα+1(Ω))中弱*收敛到u;

③Bmk在空间L∞(τ,T;V)∩L∞(τ,T;Lβ+1(Ω))中弱*收敛到B;

④ξmk在空间L2(τ-h,T;V)中强收敛到ξ.

由ξmk于空间L2(τ-h,T;H)强收敛到ξ及假设条件(iv)可知,g1(·,um)于空间L2(τ,T;H)强收敛到g1(·,u),g2(·,Bm)于空间L2(τ,T;H)强收敛到g2(·,B).

下面证明解的唯一性.

故有

由引理2可得