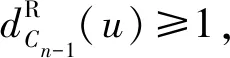临界完全图Ramsey数

李 燕， 李雨生

(同济大学 数学科学学院， 上海 200092)

1 研究背景

文中研究的图均为简单图.设G和H是任意的两个图.Ramsey数r(G,H)定义为最小的正整数r，使得图Kr的任意红蓝二边着色或存在单色的红色子图G，或存在单色的蓝色子图H.实际上，在Ramsey数的研究中，并不需要完全图的所有边即可找到单色的红色子图G或单色的蓝色子图H.因此，Hook等[1]首先在文献[1]中提出临界星图Ramsey数r*(G,H)并确定了一些临界星图Ramsey数.下面给出临界星图Ramsey数的定义.

定义1设r=r(G,H)为Ramsey数，临界星图Ramsey数r*(G,H)定义为最小的正整数n，使得图Kr-K1,r-1-n的任意红蓝二边着色或存在单色的红色子图G，或存在单色的蓝色子图H.

临界星图Ramsey数是在完全图中删掉最大星图的导出子图中寻找单色红色子图G或单色蓝色子图H.进一步发现，在寻找Ramsey数的过程中，完全图Kr的边可以在删掉星图后继续减少，仍然可能存在单色红色子图G或单色蓝色子图H.

定义2设r=r(G,H)为Ramsey数，临界完全图Ramsey数为最大的正整数n，使得图Kr-Kn的任意红蓝二边着色或存在单色的红色子图G或存在单色的蓝色子图H.

2 主要结果的证明

引理1[5]当整数n≥5，r(W1,n,K3)=2n+1.

引理2[6]当整数n≥4，r(Cn,K3)=2n-1.

引理3[2]当整数n≥3，r*(Cn,K3)=n+1.当整数n≥5，r*(W1,n,K3)=n+3.