一类带次线性中立项和分布时滞的三阶阻尼微分方程的振动性
2024-01-17林文贤
林 文 贤
(韩山师范学院 数学与统计学院, 广东 潮州 521041)
0 引 言
考虑具有分布时滞和阻尼项的三阶中立型微分方程:
的振动性, 且满足下列条件:
(H1) 0<μ≤1,κ≥1,μ,κ均为两个正奇数之商;
(H6)G(x,ξ,v)∈C([x0,∞)×[a,b]×(0,∞),(0,∞)),m(x,ξ)∈C([x0,∞)×[a,b],(0,∞)),G(x,ξ,v)/vκ≥m(x,ξ);
令
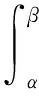
(2)
若函数y(x)满足方程(1)及y(x)∈C1([Ty,∞),(-∞,+∞)),p(x)[z(x)(w′(x))κ]′∈C1[Ty,∞),Ty≥t0, 则称y(x)是方程(1)的一个解.若y(x)既非最终为正, 也非最终为负, 则称y(x)在[Ty,∞)上振动; 否则, 称y(x)是非振动的.
由于中立型微分方程广泛应用于自然科学和应用技术等领域, 因此关于三阶中立型微分方程解的振动性和渐近性研究备受关注[1-12].文献[3]研究了三阶方程
(a(x)(b(x)(y(x)+py(x-τ))′)′)′+q(x)f(y(x-σ))=0
的振动性; 文献[7]研究了具连续分布滞量的三阶微分方程
的振动性; 文献[8]研究了方程(1)当μ=κ=1及Z(x)恒为1时特例的振动性; 文献[10]研究了三阶阻尼微分方程
[r(t)([x(t)+p(t)x(τ(t))]″)α]′+m(t)([x(t)+p(t)x(τ(t))]″)α+q(t)f(x(σ(t)))g(x′(t))=0
的振动性; 文献[11]研究了方程(1)当μ=κ=1时特例的振动性, 得到了若干解的振动性定理.
本文受文献[7-10]的启发, 考虑中立型方程(1)当0<μ≤1和κ≥1时更广泛的情形, 给出该方程的振动性条件及实例.
1 引 理
引理1若y(x)是方程(1)的正解, 则当x≥x1≥x0时有下列两种可能:
1)w(x)>0,w′(x)>0, (z(x)[w′(x)]κ)′>0;
2)w(x)>0,w′(x)<0, (z(x)[w′(x)]κ)′>0.
证明: 首先, 设y(x)是方程(1)在[x0,∞)上的一个正解, 由条件(H4)和(H5)知, 存在x1>x0, 使得当x≥x1时, 有y(τ(x,t))>0,y(σ(x,ξ))>0.于是由式(2)和条件(H3)有w(x)>y(x)>0.
其次, 由方程(1)和条件(H6)有
因此可得
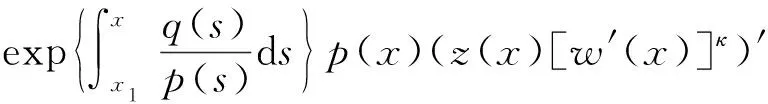
(z(x)[w′(x)]κ)′<0或(z(x)[w′(x)]κ)′>0.
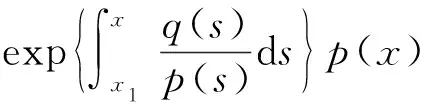
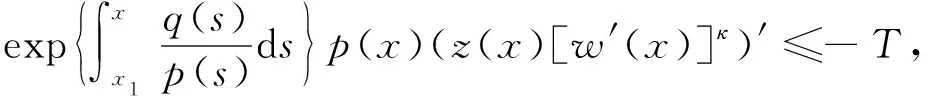
(3)
将式(3)从x2到x积分得
令x→∞, 由条件(H1)得z(x)[w′(x)]κ→-∞.因此由(z(t)[w′(x)]κ)′≤0, 可知当x≥x3≥x2时,
z(x)[w′(x)]κ≤z(x3)[w′(x3)]κ<0,
从而有

(4)
对式(4)从x3到x积分, 有
令x→∞, 由条件(H2)可得w(x)→-∞, 与w(x)>0矛盾, 进而有(z(x)[w′(x)]κ)′>0.证毕.
引理2设y(x)是方程(1)的最终正解,w(x)满足引理1中结论2), 若
在信息网络、社交网络和价值网络组合效应之下,互联网内容创作模式主要演化为三种形式。主要包括PGC(精英生产内容)、UGC(用户生产内容)和OGC(机构生产内容)模式。PGC和OGC模式是融媒体内容生产的主流,但互联网平台鼓励UGC模式,这也是缩减平台内容生产成本、保持平台长久生命力的主要策略。融媒体中心内容体系建设需要有机组合三者,从中整合筛选出符合主流价值观的内容。这就要求中心能够为内容生产者提供更具活力的创作环境,给予网民更多的包容。
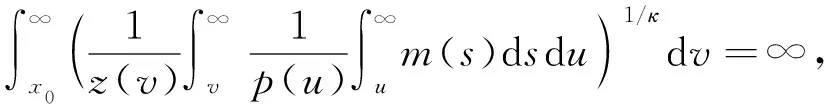
(5)

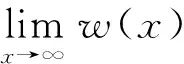


(α(x)p(x)(z(x)[w′(x)]κ)′)′≤-Kκα(x)wκ(σ(x,b))m(x).
(7)
对式(7)在(x,+∞)上积分, 有

再注意到w(σ(x,b))>j和w′(x)>0, 有
从而
进而有

(8)
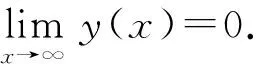
引理3[13]设0<λ≤1, 则:
1)Xλ+Yλ≤21-λ(X+Y)λ,X,Y为非负实数;
2) (1+X)λ≤1+λX, 其中1+X>0.
2 主要结果
下面利用Riccati变换和文献[14]中的一些估计, 证明方程(1)的一些新的振动性结果. 记
E={(x,s)|x≥s≥x0},E0={(x,s)|x>s≥x0}.
如果函数J(x,s)∈C(E,R)具有下列性质, 则称J(x,s)属于Y类, 记作J∈Y:
(i)J(x,x)=0,x≥x0,J(x,s)>0, (x,s)∈E0;
(iii) 存在函数f(x,s)∈C(E,R), 使得
定理1设式(5)成立, 且存在函数J∈Y和ψ∈C1([x0,∞),(-∞,+∞)), 使得

(9)

(10)
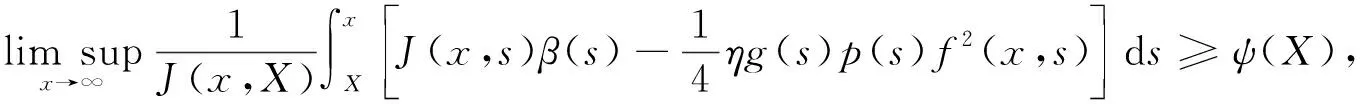
(11)
其中

(12)
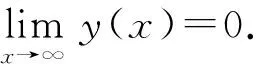
证明: 设y(x)是方程(1)的一个非振动解, 不失一般性, 设y(x)>0,x∈[x1,∞).由条件(H4),(H5)有
y(τ(x,t))>0, (x,t)∈[x1,∞)×[α,β],y(σ(x,ξ))>0, (x,ξ)∈[x1,∞)×[a,b].
当w(x)满足引理1中结论1)时, 由条件(H4),(H5), 有
由引理1中结论1)知,w(x)>0,w′(x)>0, 所以
w(σ(x,a))≥w(σ(x1,a))=k1,x≥x1.
(14)
从而由条件(H6),(H7)和上述不等式, 有


(16)
将式(16)两边乘以J(x,s), 并在[x2,x]上积分, 得
从而
于是
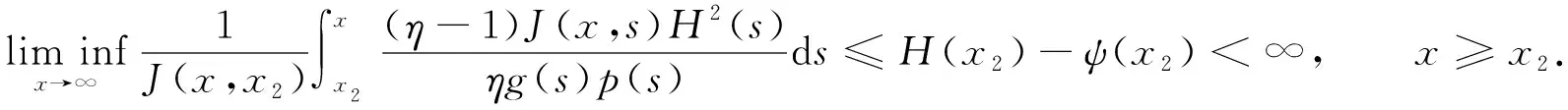
(18)


进而
于是


定理2设式(5)成立, 若存在函数J∈Y和B(x)∈C([x0,∞),(-∞,+∞)), 使得对x≥X≥x0, 满足

(19)


(20)
证明: 设y(x)是方程(1)的一个非振动解, 不失一般性, 设y(x)>0,x∈[x1,∞).由条件(H4),(H5)有
y(τ(x,t))>0, (x,t)∈[x1,∞)×[α,β],y(σ(x,ξ))>0, (x,ξ)∈[x1,∞)×[a,b].
当w(x)满足引理1中结论1)时, 令
于是


(22)
其中A(x)来自式(20).将式(22)两边乘以J(x,s), 并在[X,x]上积分得
从而有
与式(16)矛盾.

注1若方程(1)中取μ=κ=1, 则定理1和定理2即为文献[10]的振动结果, 进而改进并推广了文献[7-9]的相应结果.
3 实 例
例1考虑三阶阻尼微分方程

于是满足条件(H1)~(H7).进一步, 令
利用定理1, 有
因此满足定理1的所有条件.故由定理1知, 方程(23)的任意解振动或趋于0.
例2考虑三阶阻尼微分方程

因此满足定理2的所有条件.故由定理2知, 方程(24)的任意解振动或趋于0.
