七阶非线性薛定谔方程的调制不稳定性以及周期背景上的怪波解

姜冬竹，扎其劳，2，3

（1.内蒙古师范大学 数学科学学院，呼和浩特 010022；2.内蒙古自治区应用数学中心，呼和浩特 010022；3.无穷维哈密顿系统及其算法应用教育部重点实验室，呼和浩特 010022）

这里Φ=(ϕ1，ϕ2)T。近年来，对非线性演化方程周期怪波解的研究得到了学者们越来越多的关注。在雅可比椭圆函数［2］的背景下，利用雅可比椭圆函数展开法，结合达布变换［3］与谱问题的非线性化［4］的方法，许多非线性演化方程的周期怪波解被构造。如高阶修正Korteweg-de Vries （mKdV）方程［5］、Hirota 方程［6］、NLS 方程［7-8］。因此，本文重点是分析方程（3）的调制不稳定性。在此基础上，构造其在雅可比椭圆函数dn 和cn背景上的两类不规则的周期怪波解。

1 调制不稳定性分析

首先给出方程（3）的平面波种子解

这里A为实常数，ω表示背景频率，κ表示波数。将式（7）代入方程（3）中，可得

在式（7）中加入一个小的扰动参数ε，则扰动解可以表达成如下形式

这里r1和r2都是小参数。将式（9）代入方程（3）中，可以得到关于r1和r2的齐次线性方程组。如果令r1和r2的系数行列式结果为零，并求解关于Ω的方程组，则可求得MI 增益G为

其中

由式（10）可得，在|K|<2A的条件下G会存在虚部，则扰动函数r（x，t）呈指数增长，从而破坏了系统的稳定性并产生怪波。MI 波的宽度与参数A呈正相关，如图1 所示。

图1 方程（3）在α=-0.1，β=0.1，γ=0.1，δ=0.2 时的调制不稳定性分析Fig.1 The MI analysis of equation （3） with α=-0.1，β=0.1，γ=0.1，δ=0.2

2 雅可比椭圆函数解

3 dn 周期波和cn 周期波的特征值

4 周期特征函数与非周期解

4.1 Lax 对的周期特征函数

通过计算可得

根据式（18）、（33）、（29）和（36），得

式（38）取正或负的平方根，则以下关系可以被推出

根据式（29）和（31），以下关系可以被推导出

其满足

4.2 Lax 对的非周期解

假设Φ=(ϕ1，ϕ2)T是Lax 对式（4）-（5）在λ=λ1时的周期解，为推导怪波解，需要通过(ψ1，ψ2)T构造非周期解，其表示为Lax 对式（4）—（5）的二阶线性无关解，其形式为

其中θ=θ(x，t)是待定函数，将式（42）代入式（4），可得

根据式（12）和式（31），可以将式（43）改写为

根据式（34）和式（35），式（44）可以退化为

对式（44）关于x进行积分，得

其中θ0(t)是与t相关的积分常数。将式（42）代入式（5），利用雅可比椭圆函数展开法，得

其中

通过计算可得Δ1=0，因此

这里η是积分常数。将式（49）代入式（46）得到

5 周期背景上的怪波解

根据文献［3］，方程（3）的一重达布变换如下

其中(ϕ11，ϕ21)T为Lax 对式（4）—（5）在λ=λ1时的非零解。基于式（51）和3.1 节，应用雅可比椭圆函数dn和cn，方程（3）在周期背景上的怪波解如下

图2 当取 α=1， β=3，γ=3，δ=3，η=0 时方程（3）在dn 周期背景上的怪波解Fig.2 Rogue wave solution on the dn-periodic background of equation （3） with α=1， β=3，γ=3，δ=3，η=0

分别在k=0.5 和k=0.99 时描述方程（3）在dn 周期背景上的怪波解。特别地，当k=0 或k=1 时，可以得到dn 周期背景上的退化怪波解（见图2―5）。分别在k=0.5 和k=0.99 时描述方程（3）在cn 周期背景上的怪波解。特别地，当k=1 时，可以得到cn 周期背景上的退化怪波解（见图5―7）。

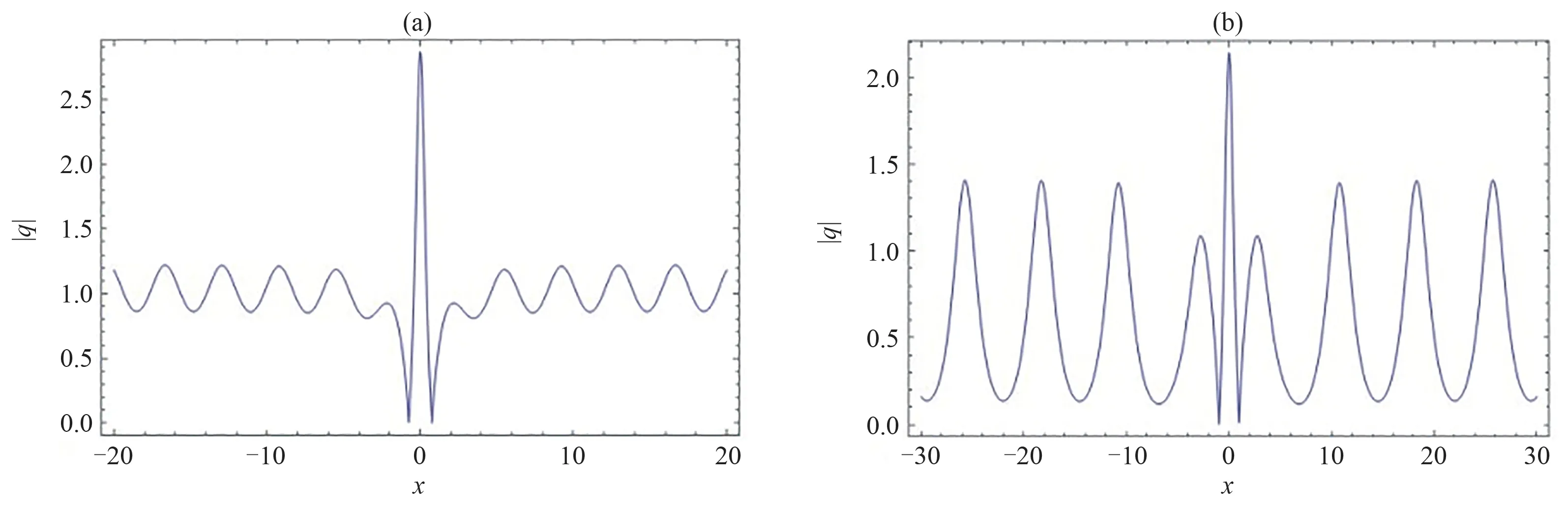
图3 当取t =0 时方程（3）在dn 周期背景上沿x 轴传播的怪波Fig.3 The wave propagation along the x-axis of rogue wave solution on the dn-periodic background of equation （3） at t =0

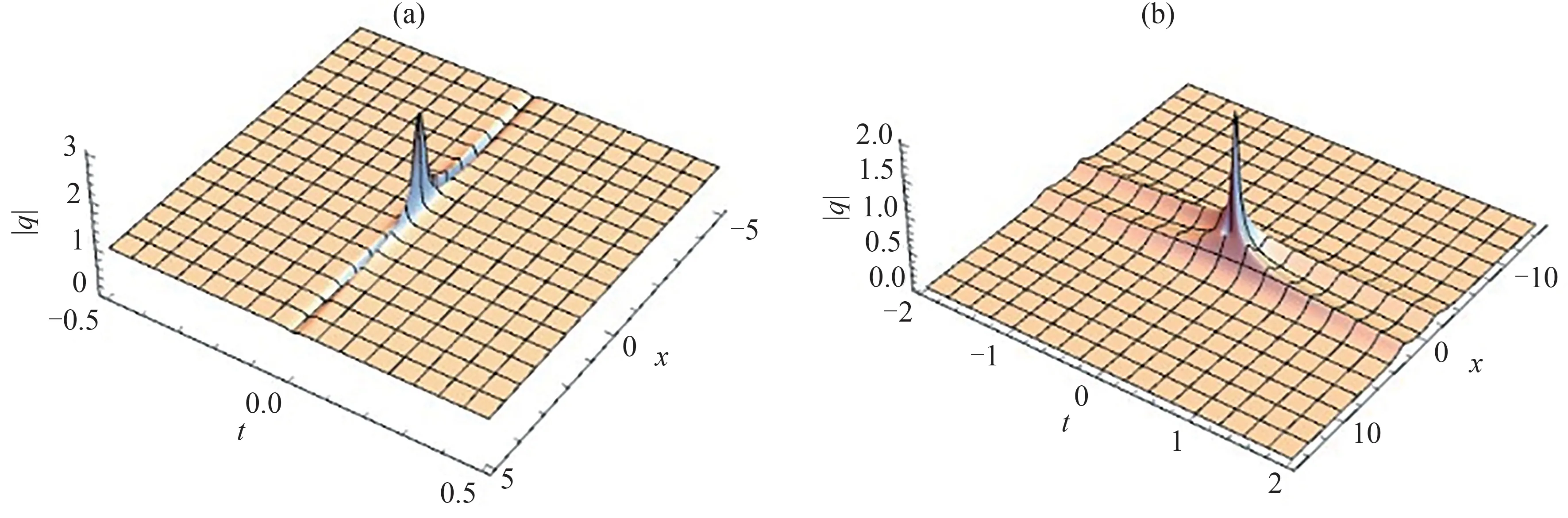
图4 当取 α=1， β=3，γ=3，δ=3，η=0 时方程（3）在dn 周期背景上的退化怪波解Fig.4 Degenerate rogue wave solution on the dn-periodic background of equation （3） with α=1， β=3，γ=3，δ=3，η=0

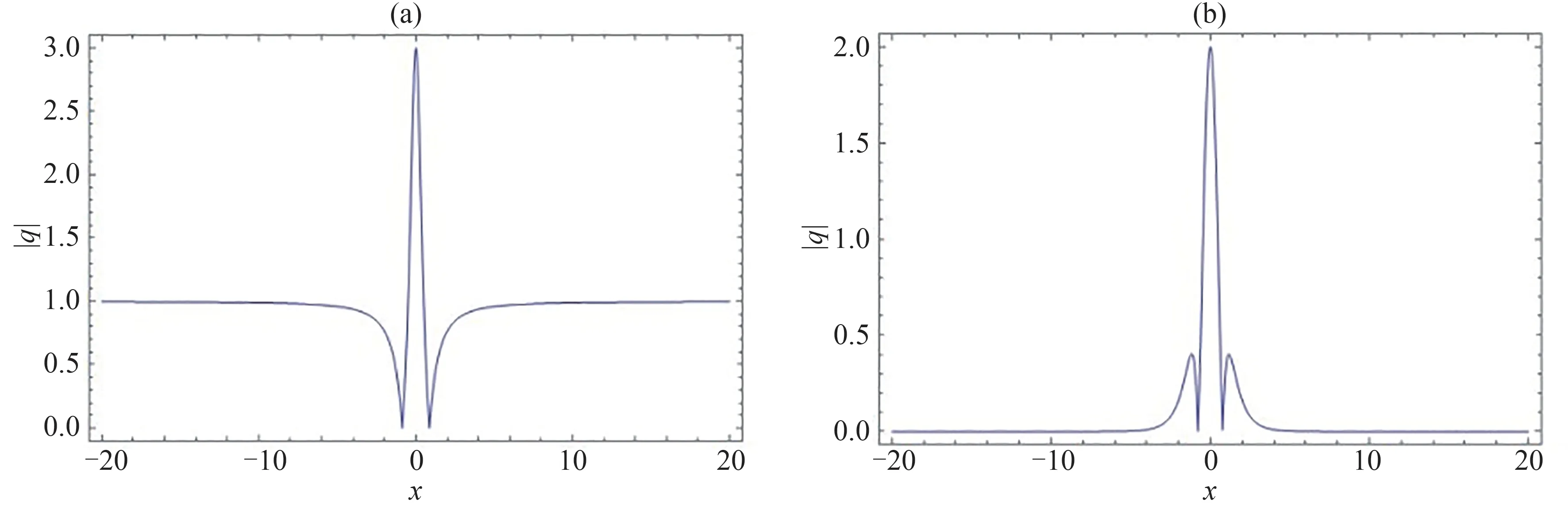
图5 当取t=0 时方程（3）在dn 周期背景上沿x 轴传播的退化怪波Fig.5 The wave propagation along the x-axis of degenerate rogue wave solution on the dn-periodic background of equation （3） at t =0

图6 当取α=1， β=3，γ=3，δ=3，η=0 时方程（3）在cn 周期背景上的怪波解Fig.6 Rogue wave solution on the cn-periodic background of equation （3） with α=1， β=3，γ=3，δ=3，η=0

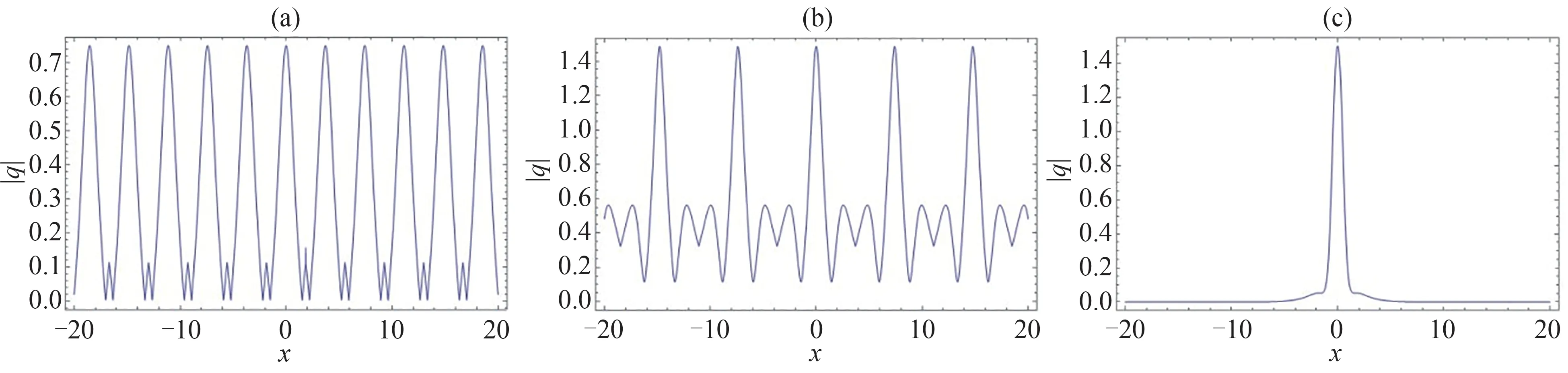
图7 当取t =0 时方程（3）在cn 周期背景上沿x 轴传播的怪波Fig.7 The wave propagation along the x-axis of degenerate rogue wave solution on the cn-periodic background of equation （3） at t =0

6 结论

本文在分析调制不稳定性的基础上，通过引入巴格曼约束，利用谱问题的非线性特性和达布变换方法，构造七阶非线性薛定谔方程在dn 和cn 背景上的不规则周期怪波，并通过图像显示了它们的动力学特性。此外，在雅可比椭圆函数的背景上，雅可比椭圆函数展开法简化了推导过程，显示了该方法在计算过程中的便捷性。