关于不定方程x2-3y4=p(p=13,37,61,73)
2023-02-26管训贵
管训贵
(泰州学院 数理学院,江苏 泰州 225300)
0 引言
设D,M为给定的整数,且D>0为非平方数,N(D,M)表示不定方程
x2-Dy4=M
(1)
的正整数解的个数。
文献[1]首先证明了N(5,44)=1,N(5,11)=2,N(5,-44)=3。后来,文献[2]证明了N(3,46)=2;文献[3]证明了N(3,22)=2;文献[4]证明了N(3,97)=1;文献[5]证明了N(3,166)=2;文献[6]证明了N(3,286)=2;文献[7]证明了N(7,93)=2;文献[8]证明了N(2,17)=2,N(2,41)=0,N(2,73)=0,N(2,89)=2,N(2,97)=0。当N(D,M)≥1时,文献[1-8]均给出了方程(1)的全部正整数解。
1 主要结论
本文对D=3,M=p为奇素数且p<100的情形进行探究,发现仅当p=13,61,73和97时,式(1)有正整数解,对于其他的p,式(1)均无正整数解。由于p=3,5,11,17,23,29,41,47,53,59,71,83,89时,模3知不可能;p=7,19,31,43,67,79时,方程x2-3y2=p无基本解;且p=97已在文献[4]中解决。故只需考虑p=13,37,61,73的情形。
利用递归序列、同余式以及平方剩余的有关性质,证明了如下结果。
定理1N(3,13)=2;(x,y)=(4,1),(16,3)。
定理2N(3,37)=0。
定理3N(3,61)=2;(x,y)=(8,1),(44,5)。
定理4N(3,73)=2;(x,y)=(11,2),(29,4)。
2 定理的证明
2.1 定理1的证明
设相应的不定方程为
x2-3y4=13。
(2)
易知,方程X2-3Y2=13的一般解可由以下2个非结合类给出:
或
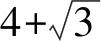
若式(2)有整数解,必有n使得
y2=±(un+4vn)或y2=±(un-4vn)=±(u-n+4v-n),
当n≥0时,un+4vn>0;当n<0时,un+4vn<0。因此可归结为
y2=un+4vn,n≥0
(3)
或
y2=-un+4vn,n>0。
(4)
容易验证下列关系:
un+2=4un+1-un,u0=1,u1=2;
(5)
vn+2=4vn+1-vn,v0=0,v1=1;
(6)
un+r=unur+3vnvr,vn+r=unvr+vnur;
(7)
(8)
(9)
un+2kr≡(-1)kun(modur),vn+2kr≡(-1)kvn(modur)。
(10)
先讨论式(3)。(为节省篇幅,下文中的“T”表示取模后所得剩余序列的周期)
当式(3)成立时,利用(5)、(6)两式对式(3)取模4得T=4,且当n≡1,2,3(mod 4)时,un+4vn≡2,3,2(mod 4)均为4的平方非剩余,故排除,剩n≡0(mod 4)。
对式(3)取模5得T=3,且当n≡2(mod 3)时,un+4vn≡3(mod 5)为5的平方非剩余,故排除,剩n≡0,1(mod 3),即n≡0,1,3,4,6,7,9,10,12,13(mod 15)。
对式(3)取模29得T=15,且当n≡4,7,10(mod 15)时,un+4vn≡2,11,19(mod 29)均为29的平方非剩余,故排除,剩n≡0,1,3,6,9,12,13(mod 15)。
对式(3)取模19得T=5,且当n≡3(mod 5)时,un+4vn≡10(mod 19)为19的平方非剩余,故排除n≡3,13(mod 15),剩n≡0,1,6,9,12(mod 15),结合n≡0(mod 4),得n≡0,16,36,24,12(mod 60)。
对式(3)取模61得T=60,且当n≡12,16,36(mod 60)时,un+4vn≡18,23,43(mod 61)均为61的平方非剩余,故排除,剩n≡0,24(mod 60),从而n≡0(mod 3),即n≡0,3,6(mod 9)。
对式(3)取模53得T=9,且当n≡3,6(mod 9)时,un+4vn≡33,19(mod 53)均为53的平方非剩余,故排除,剩n≡0(mod 9),结合n≡0(mod 4),得n≡0(mod 36)。
若n≠0,令n=0+2×3t(6l±2)(t≥2),并取m=3t,此时m≡9(mod 18),则由式(3)结合式(10)得
y2=un+4vn≡-(u∓2m+4v∓2m)≡-(u2m∓4v2m)(modu3m)。
(11)


当式(4)成立时,利用(5)、(6)两式对式(4)取模4得T=4,且当n≡0,1,3(mod 4)时,-un+4vn≡3,2,2(mod 4)均为4的平方非剩余,故排除,剩n≡2(mod 4),即n≡2,6,10,14,18,22,26(mod 28)。
对式(4)取模2 521得T=28,且当n≡6,10,18,26(mod 28)时,-un+4vn≡1 769,321,2 394,2 498均为2 521的平方非剩余,故排除,剩n≡2,14,22(mod 28),从而n≡2,0,1(mod 7)。
对式(4)取模71得T=7,且当n≡0(mod 7)时,-un+4vn≡70(mod 71)为71的平方非剩余,故排除,剩n≡1,2(mod 7),即n≡1,2,8,9,15,16(mod 21)。
对式(4)取模2 017得T=21,且当n≡8,15,16(mod 21)时,-un+4vn≡435,1 580,819(mod 2 017)均为2 017的平方非剩余,故排除,剩n≡1,2,9(mod 21)。
对式(4)取模5得T=3,且当n≡1(mod 3)时,-un+4vn≡2(mod 5)为5的平方非剩余,故排除n≡1(mod 21),剩n≡2,9(mod 21),从而n≡2(mod 7)。结合n≡2(mod 4)得n≡2(mod 28)。
若n≠2,令n=2+2×2×7×3t(3l±1)(t≥0),并取m=2×7×3t,此时m≡14,42(mod 56),则由式(4)结合(7)、(10)两式得
y2=-un+4vn≡±(-u2∓2m+4v2∓2m)≡±(-9u2m±16v2m)(modu3m),
于是有
(12)


综上,方程(2)仅有正整数解(x,y)=(4,1),(16,3)。
2.2 定理2的证明
设相应的不定方程为
x2-3y4=37。
(13)
易知,方程X2-3Y2=37的一般解可由以下2个非结合类给出:
或

若方程(13)有整数解,必有n使得
y2=±(2un+7vn)或y2=±(2un-7vn)=±(2u-n+7v-n)。
当n≥0时,2un+7vn>0;当n<0时,2un+7vn<0。因此可归结为
y2=2un+7vn,n≥0
(14)
或
y2=-2un+7vn,n>0。
(15)
当式(14)成立时,利用(5)、(6)两式对式(14)取模5得T=3,且当n≡0,2(mod 3)时,2un+7vn≡2(mod 5)为5的平方非剩余,故排除,剩n≡1(mod 3),即n≡1,4,7(mod 9)。
对式(14)取模53得T=9,且当n≡4,7(mod 9)时,2un+7vn≡3,39(mod 53)均为53的平方非剩余,故排除,剩n≡1(mod 9),即n≡1,10(mod 18)。
对式(14)取模17得T=18,且当n≡1,10(mod 18)时,2un+7vn≡11,6(mod 17)均为17的平方非剩余,故排除,因此式(14)不成立。
当式(15)成立时,利用(5)、(6)两式对式(15)取模5得T=3,且当n≡0,1(mod 3)时,-2un+7vn≡3(mod 5)为5的平方非剩余,故排除,剩n≡2(mod 3),即n≡2,5,8(mod 9)。
对式(15)取模53得T=9,且当n≡2,5(mod 9)时,-2un+7vn≡14,50(mod 53)均为53的平方非剩余,故排除,剩n≡8(mod 9),即n≡8,17(mod 18)。
对式(15)取模17得T=18,且当n≡8,17(mod 18)时,-2un+7vn≡11,6(mod 17)均为17的平方非剩余,故排除,因此式(15)不成立。
综上,方程(13)无正整数解。
2.3 定理3的证明
设相应的不定方程为
x2-3y4=61。
(16)
易知,方程X2-3Y2=61的一般解可由以下2个非结合类给出:
或

若方程(16)有整数解,必有n使得y2=±(un+8vn)或y2=±(un-8vn)=±(u-n+8v-n)。当n≥0时,un+8vn>0;当n<0时,un+8vn<0。 因此可归结为
y2=un+8vn,n≥0
(17)
或
y2=-un+8vn,n>0。
(18)
当式(17)成立时,利用(5)、(6)两式对式(17)取模8得T=4,且当n≡1,2,3(mod 4)时,un+8vn≡2,7,2(mod 8)均为8的平方非剩余,故排除,剩n≡0(mod 4),即n≡0,4,8(mod 12)。
对式(17)取模3得T=6,且当n≡4(mod 6)时,un+8vn≡2(mod 3)为3的平方非剩余,故排除n≡4(mod 12),剩n≡0,8(mod 12)。
对式(17)取模37得T=36,且当n≡8,20,32(mod 36)时,un+8vn≡20,35,19(mod 37)均为37的平方非剩余,故排除n≡8(mod 12),剩n≡0(mod 12)。
若n≠0,令n=0+2×3t(6l±2)(t≥1),并取m=3t,此时m≡3,9(mod 12),则由式(17)结合式(10)得
y2=un+8vn≡-(u∓2m+8v∓2m)≡-(u2m∓8v2m)(modu3m)。
(19)


当式(18)成立时,利用(5)、(6)两式对式(18)取模8得T=4,且当n≡0,1,3(mod 4)时,-un+8vn≡7,6,6(mod 8)均为8的平方非剩余,故排除,剩n≡2(mod 4),即n≡2,6(mod 8)。
对式(18)取模7得T=8,且当n≡6(mod 8)时,-un+8vn≡3(mod 7)为7的平方非剩余,故排除,剩n≡2(mod 8)。
又由n≡2(mod 4)得n≡2,6,10(mod 12)。
对式(18)取模3得T=6,且当n≡0(mod 6)时,-un+8vn≡2(mod 3)均为3的平方非剩余,故排除n≡6(mod 12),剩n≡2,10(mod 12),即n≡2,10,14,22,26,34(mod 36)。
对式(18)取模37得T=36,且当n≡10,22,26,34(mod 36)时,-un+8vn≡20,19,22,35(mod 37)均为37的平方非剩余,故排除,剩n≡2,14(mod 36),故n≡2(mod 3),结合n≡2(mod 8)得n≡2(mod 24)。
若n≠2,令n=2+2×3×2t×(2l+1)(t≥2),并取
此时,m≡1,4(mod 5),则由式(18)结合(7)、(10)两式得
y2=-un+8vn≡±(-u2+2m+8v2+2m)≡±(25u2m+44v2m)≡±44v2m(modu2m)。
(20)
注意到4|m时,u2m≡um≡1(mod 8),um≡1(mod 3),结合(8)、(20)两式给出

综上,方程(16)仅有正整数解(x,y)=(8,1),(44,5)。
2.4 定理4的证明
设相应的不定方程为
x2-3y4=73。
(21)
易知,方程X2-3Y2=73的一般解可由以下2个非结合类给出:
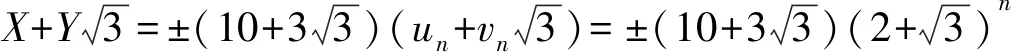
或

若方程(21)有整数解,必有n使得
y2=±(3un+10vn)或y2=±(3un-10vn)=±(3u-n+10v-n),
当n≥0时,3un+10vn>0;当n<0时,3un+10vn<0。 因此可归结为
y2=3un+10vn,n≥0
(22)
或
y2=-3un+10vn,n>0。
(23)
当式(22)成立时,利用(5)、(6)两式对式(22)取模5得T=3,且当n≡0(mod 3)时,3un+10vn≡3(mod 5)为5的平方非剩余,故排除,剩n≡1,2(mod 3),即n≡1,2,4,5(mod 6)。
对式(22)取模3得T=6,且当n≡4,5(mod 6)时,3un+10vn≡2(mod 3)为3的平方非剩余,故排除,剩n≡1,2(mod 6),即n≡1,2,7,8,13,14,19,20(mod 24)。
对式(22)取模193得T=24,且当n≡2,7,8,14,19,20(mod 24)时, 3un+10vn≡61,39,76,132,154,117(mod 193)均为193的平方非剩余,故排除,剩n≡1,13(mod 24)。
对式(22)取模7得T=8,且当n≡5(mod 8)时,3un+10vn≡5(mod 7)为7的平方非剩余,故排除n≡13(mod 24),剩n≡1(mod 24)。
若n≠1,令n=1+2×3×2t×(4l±1)(t≥2),并取m=3×2t,此时m≡12,9,3,6(mod 15),则由式(22)结合(7)、(10)两式得
y2=3un+10vn≡3u1±2m+10v1±2m≡16u2m±29v2m≡±29v2m(modu2m)。
(24)
又4|m时,um≡1(mod 4),u2m≡1(mod 8),设2s‖vm,则有
由式(24)得

当式(23)成立时,仿式(22)的讨论,对式(23)分别取模5,排除n≡0(mod 3);取模3,排除n≡4,5(mod 6);取模193,排除n≡2,7,8,14,19,20(mod 24);取模7,排除n≡13(mod 24),最后剩n≡1(mod 24)。
若n≠1,令n=1+2×3×2t×(4l±1)(t≥2),并取
此时m≡1,4(mod 5),则由式(23)结合(7)、(10)两式得
y2=-3un+10vn≡-3u1±2m+10v1±2m≡4u2m±11v2m≡±11v2m(modu2m)。
(25)


综上,方程(21)仅有正整数解(x,y)=(11,2),(29,4)。
