Mg80Sc20 合金非线性形变的计算研究

赵继颖，周 游，孙霖评，武晓霞，那日苏，2

（1.内蒙古师范大学 物理与电子信息学院，内蒙古 呼和浩特 010022；2.内蒙古自治区功能材料物理与化学重点实验室，内蒙古 呼和浩特 010022）

金属结构材料的高强度和优异延展性是两个重要的力学特性。因此，研究人员一直致力于开发具有良好延展性的高强度结构材料。在实际应用中，这些材料的强度和延展性往往受到位错、裂纹和晶界等缺陷相关的复杂微观结构特征的影响［1］。如果这些缺陷不存在，材料的强度会受到应力的限制。当施加足够大的应力时，晶格会变得不稳定，而晶格所能承受的最大应力即为理想强度。理想强度是材料的一种固有性质，它提供了材料强度的理论上限，是理想单晶可能达到的最大强度。理想强度可以通过实验测量并使用第一性原理方法计算，它可以揭示化学键与晶体对称性之间的关系，同时也是少数可以用来描述单晶材料的基本力学参数之一［2-4］。

镁合金的密度较低，是最轻的实用合金。镁具有较高的比强度和比刚度，阻尼性能良好，有强大的电磁屏蔽能力，并且在铸造和切削加工方面性能优越，一直受到广泛关注［5］。然而，传统镁合金由于其六方密排（hcp）结构，具有较高的塑性各向异性，在室温下塑性较差，限制了其实际应用。相比之下，含有少量稀土元素的二元镁合金，如MgCe 和MgY 合金，伸长率要高得多，但强度与纯镁一样低［6］。这些事实表明，具有hcp 结构的镁合金不能同时表现出高强度和高塑性。因此，开发具有各向同性晶体结构的镁合金是必要的。在所有Mg-X 二元体系中，只有MgLi 和MgSc 合金具有体心立方（bcc）结构的β相［6-7］。由于bcc 结构中存在更多的滑移系，因此能够在各个方向上表现出更好的塑性变形能力。

Ogawa 等［8］发现β相Mg-20.5 at.% Sc 合金由应力诱导的马氏体相变而表现出形状记忆效应和超弹性等形状记忆特性。这种镁合金密度约为2 g/cm3，比TiNi 形状记忆合金低三分之一。Mg-20.5 at.% Sc 合金的最大超弹性应变约为4.4%，但仅在约-150oC 的低温下才能实现，从而限制了该合金的实际应用。研究表明，马氏体相变温度与Sc 含量密切相关，且随Sc 含量的降低而升高。Yamagishi 等［9］研究Mg-18.7 at.% Sc的应力应变行为，将合金材料在室温下通过循环拉伸实验，在Mg-18.7 at.% Sc 中发现了室温超弹性。Raghuraman等［10］研究了纯Nb 和Mo 沿［001］晶向的拉伸性质，所施加工程应变范围为-10%～70%。发现开始拉伸时，bcc结构的Nb 和Mo 首先转变为四方结构，随着进一步的拉伸，对称性被打破，结构发生正交转变，最后在工程应变为41.4% 时又转回了bcc 结构。Li 等［11］研究了面心立方（fcc）结构的Fe45Co25Ni10V20高熵合金在低温下的拉伸变形行为，发现其具有高达1.1 GPa 的抗拉强度，同时保持82% 的超高断裂伸长率，并阐明这种现象是由变形诱导的fcc 到bcc 马氏体转变引起的。Yamagishi 等［12］研究了bcc MgSc 合金在室温下的变形行为，发现当Sc 含量从19.4% 增加到19.8% 时，MgSc 合金在室温下的变形行为由超弹性转变为相变诱导塑性（TRIP），这是由于Sc 的加入稳定了合金的β相。由超弹性转变为TRIP 效应的Sc 含量阈值为19.5 at%，且TRIP MgSc合金的断裂应变范围在45%～66% 之间，极限抗拉强度可达220 MPa 以上。由于多晶样品在经历大拉伸时，局域晶粒可能会发生非常大的拉伸或塑性形变。因此，本文研究bcc MgSc 合金在大拉伸变形下的性质，评估其强度和塑性特性。

1 理论基础与计算方法

1.1 理想强度计算方法

首先，需要通过弛豫计算得到材料在基态结构下的平衡晶格参数；其次，需沿特定方向施加应力，对应每个应变值，垂直于施加应力的方向进行充分弛豫，充分考虑各向异性泊松效应；最后，对数据进行拟合即可得到能量-应变曲线。通过对能量-应变关系进行相关计算，可以获得应力-应变曲线。应力可根据

计算得到［13］。其中E为单原子能量；Ω(ϵ)为给定应变下单原子的体积；ϵ为沿特定轴拉伸时的工程应变，其定义为

其中l0和l分别表示晶格常数c在初态和末态下与外力平行方向上的长度［14］。

1.2 能量计算方法

采用密度泛函理论的从头计算方法［15-17］，使用广义梯度近似的PBE（perdew-burke-ernzerhof，PBE）泛函［18］来处理交换关联效应，利用EMTO［19-21］（exact muffin-tin orbital，EMTO）方法求解Kohn-Sham 方程。利用相干势近似（coherent potential approximation，CPA）［22］处理合金中的化学无序问题，并通过全电荷密度（full charge density，FCD）技术修正总能量，确保计算结果的准确性［21-22］。对垂直于施加应力方向弛豫过程中，K点取值均为11×11×14，能量收敛标准为10-8Ry。

2 结果与讨论

MgSc 合金结构如图1 所示，其中图1（a）为体心立方（bcc）结构的Mg80Sc20的合金图，A，B，C向量分别与bcc 晶胞的［100］、［010］和［001］晶向平行。将bcc 结构Mg80Sc20合金沿［001］晶向拉伸时有两种可能的 形 变 路 径，一 种 是 体 心 四 方（body-centered tetragonal，bct）［23］，另 一 种 是 面 心 正 交（face-centered orthorhombic，fco）。其中bct 路径假定A，B向量的夹角γ恒为90°，探究在拉伸过程中A，B向量之间的夹角是否会发生变化，故在拉伸过程中，采用fco 路径来描述形变。在不施加应变的情况下，Mg80Sc20合金fco晶胞的晶格常数满足。沿着 ［001］ 晶向对bcc Mg80Sc20合金进行单轴拉伸，应变范围从-5% 到55%。

图2 为bcc Mg80Sc20合金晶格常数a，b随施加工程应变的变化关系图。所施加应变为零时，晶格常数a，b，c满足，它们的值分别为：a＝b＝5.084，c＝3.595。随着所施加应变的增加，晶格常数c增大，晶格常数a，b则发生不同程度的减小，但几乎是相等的，此时Mg80Sc20合金近似为四方结构，即在此阶段Mg80Sc20合金由bcc 结构转变为四方结构。在应变为25% 时，通过结构分析可以确定此时晶体的C/A比值为（此时a＝b＝c），即晶体从bct 结构转变为fcc 结构。在应变大于25% 之后，a逐渐增大，b逐渐减小，结构发生正交转变，此阶段Mg80Sc20合金结构为fco。在应变为41.4%（c/c0＝）时，对应晶格常数的值为：a＝5.087，b＝3.594，c＝5.083。将应变为零时的晶格常数值与应变为41.4% 时的晶格常数值进行对比，发现晶格常数值a基本不变，b、c值互换，bcc Mg80Sc20合金在经过41.4% 的拉伸之后似乎回到了最初的bcc 结构。图1（b）和图1（c）给出了转变前后结构的平面示意图，当沿［001］晶向拉伸至应变为41.4%时，C向量变为原来的倍。对垂直于拉伸的方向充分弛豫时，A，B向量变短，在垂直方向上观察，如图1（c）所示，经过拉伸bcc Mg80Sc20合金又回到了bcc 结构，原本的［001］轴变为［］，［110］轴变为［001］，［］轴变为［］。

图2 晶格常数随应变的变化关系Fig.2 Strain dependent changes of lattice constant

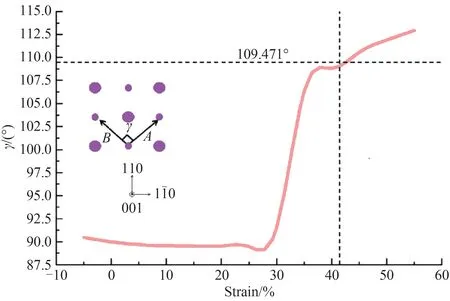
图3 γ 随应变的变化关系Fig.3 Strain dependence changes of γ

图3 为A，B向量之间的夹角γ随所施加工程应变的变化图。起初由于Mg80Sc20合金处于bct 结构，故γ一直稳定在90°左右。在应变大于25% 之后，γ快速增大，结构发生正交转变。应变为41.4% 时，γ近似为109.471°［arccos（-1/3）］，这是bcc 原始向量（连接体心原子与顶点原子的向量）之间的角度，进一步证明在拉伸过程中，bcc Mg80Sc20合金经过一系列结构变化，最终在应变为41.4% 时又回到了bcc 结构。

图4 为bcc Mg80Sc20合金的单原子能量随施加工程应变的变化关系图及对应的应力随施加工程应变的变化关系图。由图4（a）可知，应变为零时，Mg80Sc20合金的单原子能量为-0.225 5 Ry（此为约化能量）。随着沿［001］晶向的拉伸，能量会达到峰值后逐渐减小并形成一个极小值，此时形变晶胞的C/A=，晶体从bcc 转变为fcc 结构，但是这个fcc 结构不稳定。在应变为41.4% 时，Mg80Sc20合金的单原子能量与应变为零时bcc 结构的能量相同，表明此时正交结构已经恢复为bcc 结构。在整个拉伸过程中，Mg80Sc20合金首先由bcc 结构转变为四方结构，然后经历一次不稳定的fcc 转变，形成正交结构，最后又重新转回bcc结构。

应力-应变曲线上的第一个最大值定义为理想强度值。由图4（b）可知，Mg80Sc20合金在应变为6.84%左右时具有最大应力值为0.763 GPa，即为bcc Mg80Sc20合金沿［001］晶向拉伸的理想强度。随着进一步拉伸，将导致应力降低，这意味着机械不稳定［24］。当拉应力不变时，c轴会不连续地从6.84% 跳到近44%，应变范围高达37%，这也导致晶格常数的离散跳跃。

图5 电子态密度随应变的变化关系Fig.5 Variation of electronic density of states with strain

当沿［001］晶向对Mg80Sc20合金进行拉伸时，晶格结构会发生变形，电子态密度也会随之发生改变。图5 为费米能级上的电子态密度（DOS）随所施加工程应变的变化。应变为零时，费米能级上的DOS 为9.923 states/Ry，此时Mg80Sc20合金为bcc 结构，随着所施加工程应变的增加，DOS 逐渐增加，达到峰值后逐渐减小并在应变为25% 时形成一个极小值。根据以上分析可知，此极小值的出现是由于Mg80Sc20合金由bcc 结构转变为fcc 结构。应变大于25% 后，DOS 随着应变的增加而增加，在应变为41.4% 时发现此时的DOS 与应变为零时的DOS 相同，进一步证明Mg80Sc20合金在应变为41.4% 时和应变为零时合金结构相同，均为bcc 结构。通过分析DOS 随应变的变化，同样可以证实在拉伸过程中，bcc Mg80Sc20合金经历了bcc-fcc-fco-bcc 转变。

3 结论

本文通过第一性原理计算，研究了Mg80Sc20合金的非线性拉伸形变性质。详细描述在沿［001］晶向对bcc 结构Mg80Sc20合金施加单轴应变后，合金结构的转变过程。最初由bcc 结构转变为体心四方，在应变为25% 时，体心四方转变为fcc 结构，但fcc 结构并不稳定。随着所施加工程应变的继续增大，结构发生正交转变，晶格常数a≠b≠c。直到所施加工程应变达到41.4% 时，发现此时合金的能量与应变为零时的能量相等，A，B向量之间的夹角达到109.471°，同时应变为零时费米能级上的电子态密度与应变为41.4% 时费米能级上的电子态密度相等。由此证明，沿［001］晶向对bcc 结构Mg80Sc20合金进行拉伸后，当应变达到41.4% 时Mg80Sc20合金的结构经过一系列转变，又回到了bcc 结构。在多晶合金经历大拉伸形变时，个别晶粒会产生很大的形变，这些形变是通过局部晶粒的相转变实现的，发现bcc 至bcc 的转变引起非线性形变是其中一类相变引起的非线性形变。