毛管力对油藏水驱特征影响分析

2024-01-05吴桐李保柱钱其豪李冠林黎镇东

科学技术与工程 2023年34期

吴桐, 李保柱*, 钱其豪, 李冠林, 黎镇东

(1.中国石油勘探开发研究院油田开发研究所, 北京 100083;2.油气资源与探测国家重点实验室(中国石油大学(北京)石油工程学院), 北京 102249)

注水开发是目前油田最主要的开采方式之一[1]。一些油田步入特高含水期后,存在水驱无效循环现象[2]。低效无效循环过程是油藏内压力、重力和毛管力综合作用的外在表现[3]。研究揭示油水运动作用力的演化规律,明确驱油界面形成与发展的内在机理,可以为厚油层的挖潜提供明确的理论指导[4]。而对于低渗透油藏,毛管力对油水渗流规律的影响不容忽视[5]。

近些年中外针对毛管力的研究主要集中在以下两方面:一是对湿相和非湿相流体界面达到平衡状态的静态毛管力的研究,以洪世铎[6]为代表的学者研究认为,静态毛管力值受界面张力、岩石的表面润湿性及孔隙尺寸影响;二是对流体界面未到平衡状态时的毛管力研究[7],以 Hassanizadeh等[8]为代表的学者研究认为,毛管力在非稳态流动阶段会持续改变,即受到湿相流体饱和度的影响,还与湿相流体饱和度变化率相关。近些年针对毛管力对低渗储层注水开发的作用方面的研究也颇受关注,田树宝等[9]结合实验测定和数值模拟结果,探究低渗储层油水两相毛管力的动态效应,研究结果表明低渗储层毛管力的动态效应极其明显,研究结果还表明毛管力动态效应会影响对多个开采指标,其中包括水驱油前缘推进速度、沿程压力分布、见水时间、产油量和采出程度等。杨悦等[10]综合考虑了低渗油藏中启动压力梯度及毛管力影响,建立了非稳态油水相对渗透率计算方法,研究表明启动压力梯度作为油水渗流阻力,对油水相对渗透率的影响更为显著。舒卫兵等[11]利用某低渗储层23个岩心渗流曲线的数值拟合分析结果,研究表明低渗储层内存在显著的毛管力动态效应,研究结果还表明动态系数与储层的原有渗透率负相关,与润湿相的内摩擦系数正相关。马旭等[12]不仅研究了特低渗储层油水两相渗流中毛管力的动态效应同时分析了动态毛管力的影响因素,从定量角度分析了动态毛管力对储层油水两相渗流的作用,搭建并求解了特低渗储层一维水驱油模型和渗流微分方程,计算结果显示动态毛管力效应对特低渗储层的驱替效果影响显著,动态毛管力越大,驱油效果越差[13]。张振涛等[14]通过建立数值模拟理论模型,研究了动态毛管力对油藏开发动态的影响,结果表明动态毛管力造成亲油油藏含水率上升变快,产油量下降,起到阻力作用。刘广峰等[15]通过铸体薄片、恒速压汞、X衍射、核磁共振及渗流实验等多种实验手段,分析得出孔喉结构是影响致密砂岩储层渗流特征的主要因素,其中喉道半径、孔喉比及连通性等是决定储层渗流能力的关键。大喉道主要提供储层的渗流能力,而中-小孔喉则对储集能力的贡献更大。乔嘉骥[16]做了致密岩心压汞实验测量毛管力,结果表明,致密岩心微孔与中孔、大孔串联配置,孔喉细小,孔隙连通性差,进汞、退汞体积差异较大,退汞效率低,渗流空间狭小,毛管力增大,不利于致密油的渗流。Mohammed[17]采用渗透率和孔隙度几乎完全一样的岩心,采用压汞法和孔板法分别23测量其毛管力,结果表明在压力较低的区域两种方法测得的毛管力是一致的,而在压力较高的区域,由于岩心对气和水湿润性不同,所测得的结果存在差别。

油藏内注入水流动方向及波及面积与其所受合力的方向及大小有关[18]。在注水开发过程中,储层不同部位的流体所受作用力不同,不同含水时期作用力也会发生变化。现采用数值模拟方法,研究油藏各网格内流体受力状况,确定注入水在油藏内的流动特征和波及范围,从而判断出在注水开发各阶段油藏内剩余油分布特征[19]。

1 数值模拟模型及流体受力表征方法

1.1 数值模拟模型及参数设置

建立如图1和图2所示正韵律正方形储层模型,模型参数取值如表1所示,油藏顶部深度900 m,油层厚度15 m,其中上部低渗透段厚度4.5 m,渗透率30 mD;下部高渗透段厚度10.5 m,渗透率824 mD。模型外边界为封闭,无边底水侵入,在对角线布置一注一采两口井,井距175 m,注采平衡。油藏内原始含水饱和度0.34,油水密度比0.834。假设油藏内流体与岩石骨架均不可压缩,水相为润湿相,油相为非润湿相。

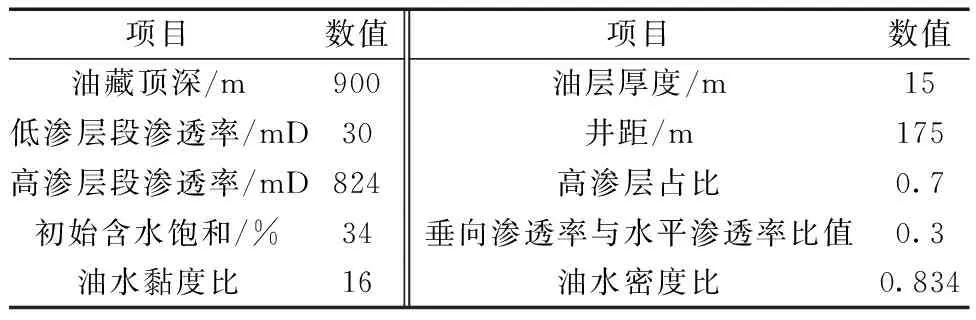
表1 模型参数表Table 1 Model parameter table

图1 模型三维示意图Fig.1 3D schematic diagram of model

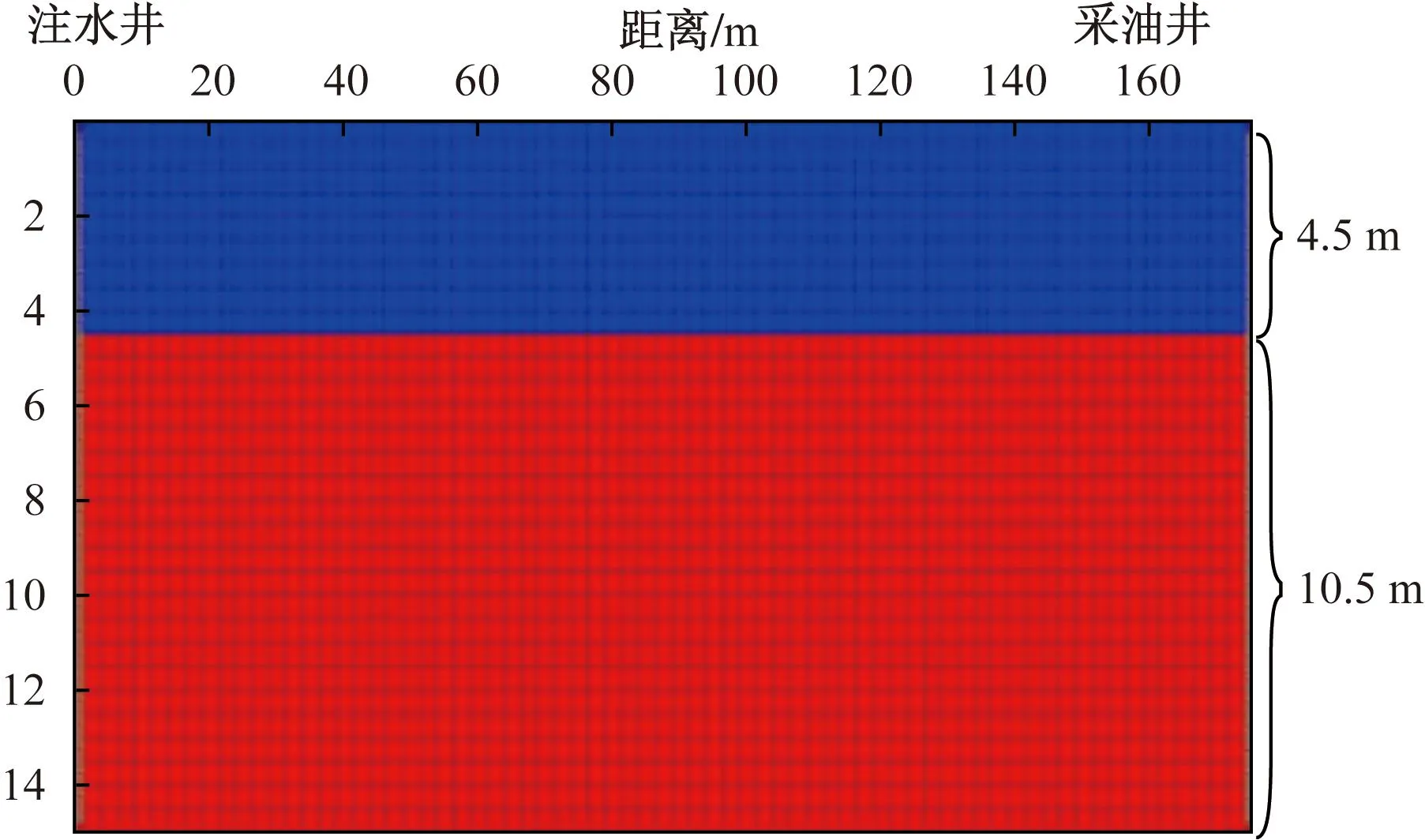
图2 模型剖面示意图(沿注采井对角线方向)Fig.2 Schematic diagram of model section (along the diagonal direction of injection production well)

1.2 储层网格流体受力表征

如图3所示,以上述模型中单元格内流体为研究对象,流体受力包括储层压力(注入水压力)Po、重力Gw和毛管力Pc。基于渗流力学理论,利用数值模拟方法,计算上述模型中各网格内流体所受作用力的大小和方向,然后利用矢量叠加得到各作用力合力的大小和方向,实现层内任意网格油水渗流作用力的定量表征,在此基础上进一步实现层内作用力场的数学描述和定量表征。

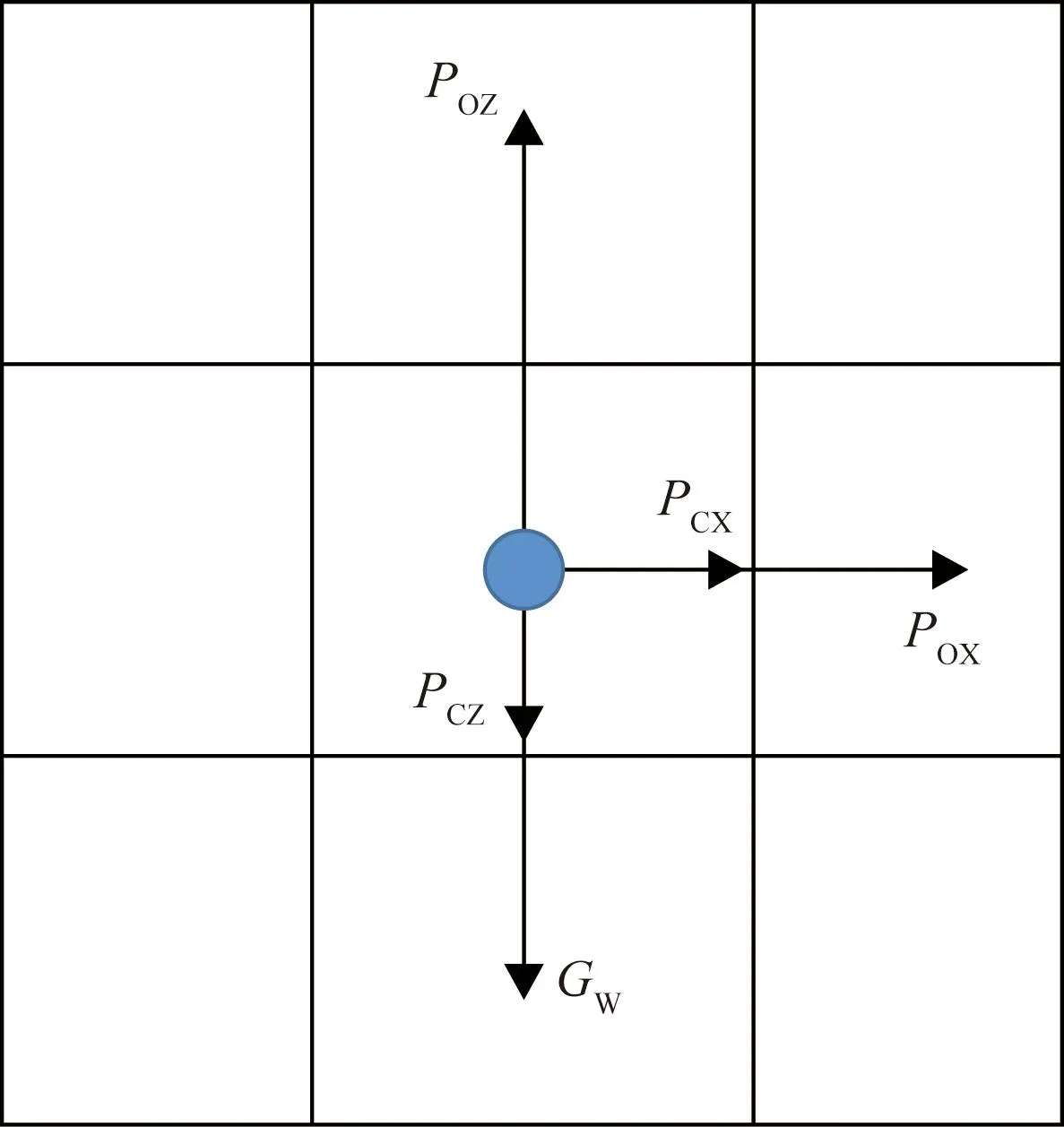
图3 储层中水质点受力示意图Fig.3 Schematic diagram of water quality point stress in reservoir

1.2.1 储层压力梯度分布表征方法

在注水开发过程中,储层压力峰值出现在注入井处,在采油井处最低,由此压力梯度在注入井与采油井之间形成,压力梯度的大小和方向由层内某点与其附近压力的相对大小决定。在数值模型中, 根据某一网格与其相邻网格的压力数值,在不同网格方向上分别求取压力梯度,基于此实现储层内各网格压力分布的数学描述[20]。

以图1中注水井所处的低渗透层角点为坐标原点,建立如图4所示坐标系,位置为(x,y,z)的单元格尺寸表示为Δx、Δy、Δz,网格面①的压力为Po·i,j,k,网格面②的压力为Po(i+1), j,k,则网格面①与②之间X方向的压力梯度可以为

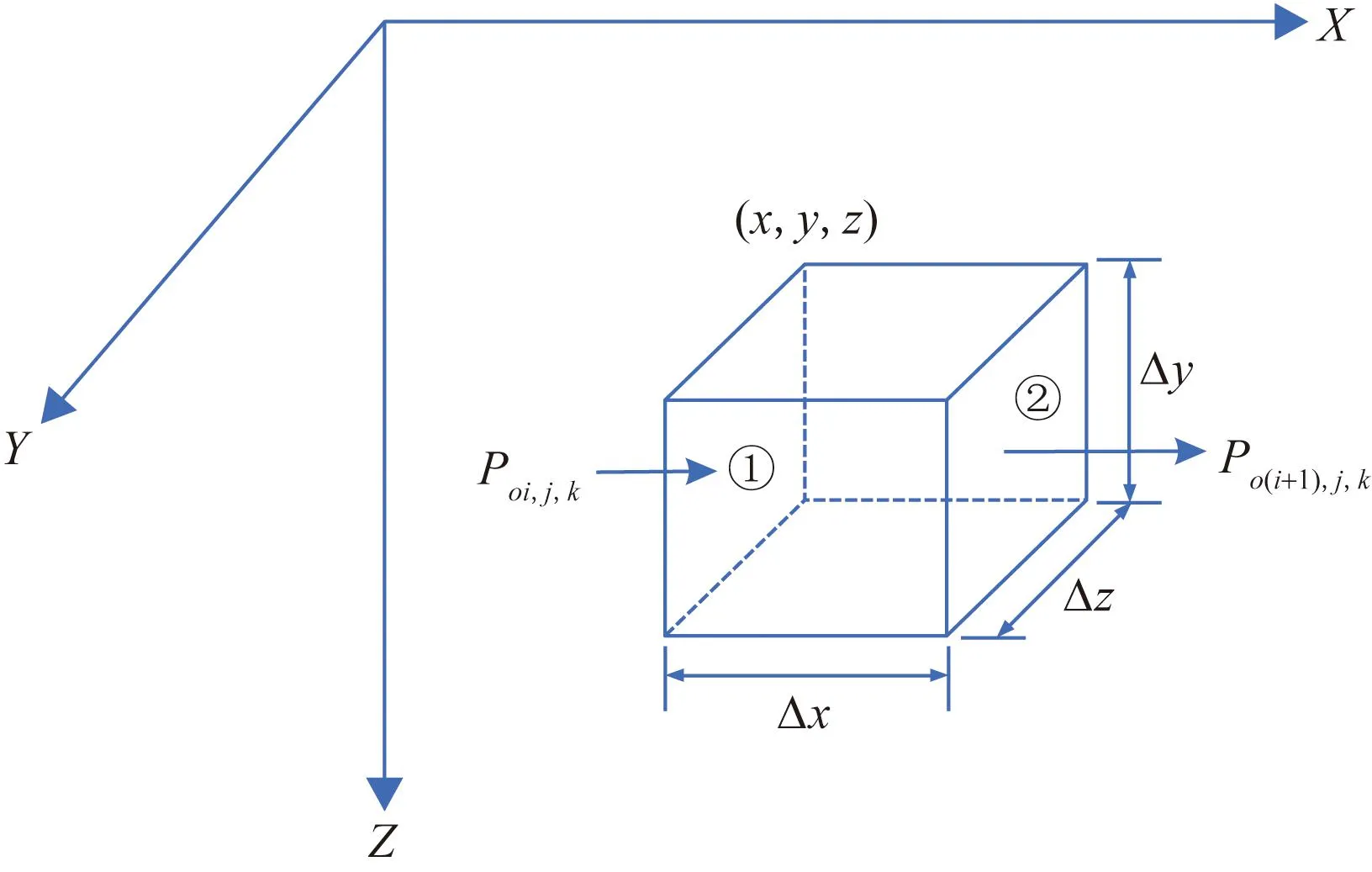
图4 X方向网格面所受压力示意图Fig.4 Schematic diagram of pressure on grid surface in X direction

(1)

同理,Y方向的压力梯度可以表示为

(2)

Z方向的压力梯度可以表示为

(3)

1.2.2 毛管力梯度分布表征方法

由于储层内各点物性及含油饱和度不同,导致其具有不同的毛管力大小和方向,从而形成层内毛管力梯度。毛管力梯度的大小和方向由层内某点与其附近毛管力的相对大小决定。在数值模型中,根据某一网格与其相邻网格的毛管力数值,在纵向和横向分别求取毛管力梯度,实现毛管力梯度分布的数学描述。

如图5所示,网格面①的毛管力为Pci,j,k,网格面②的压力为Pc(i+1),j,k,则网格面①与②间X方向的毛管力梯度可以表示为

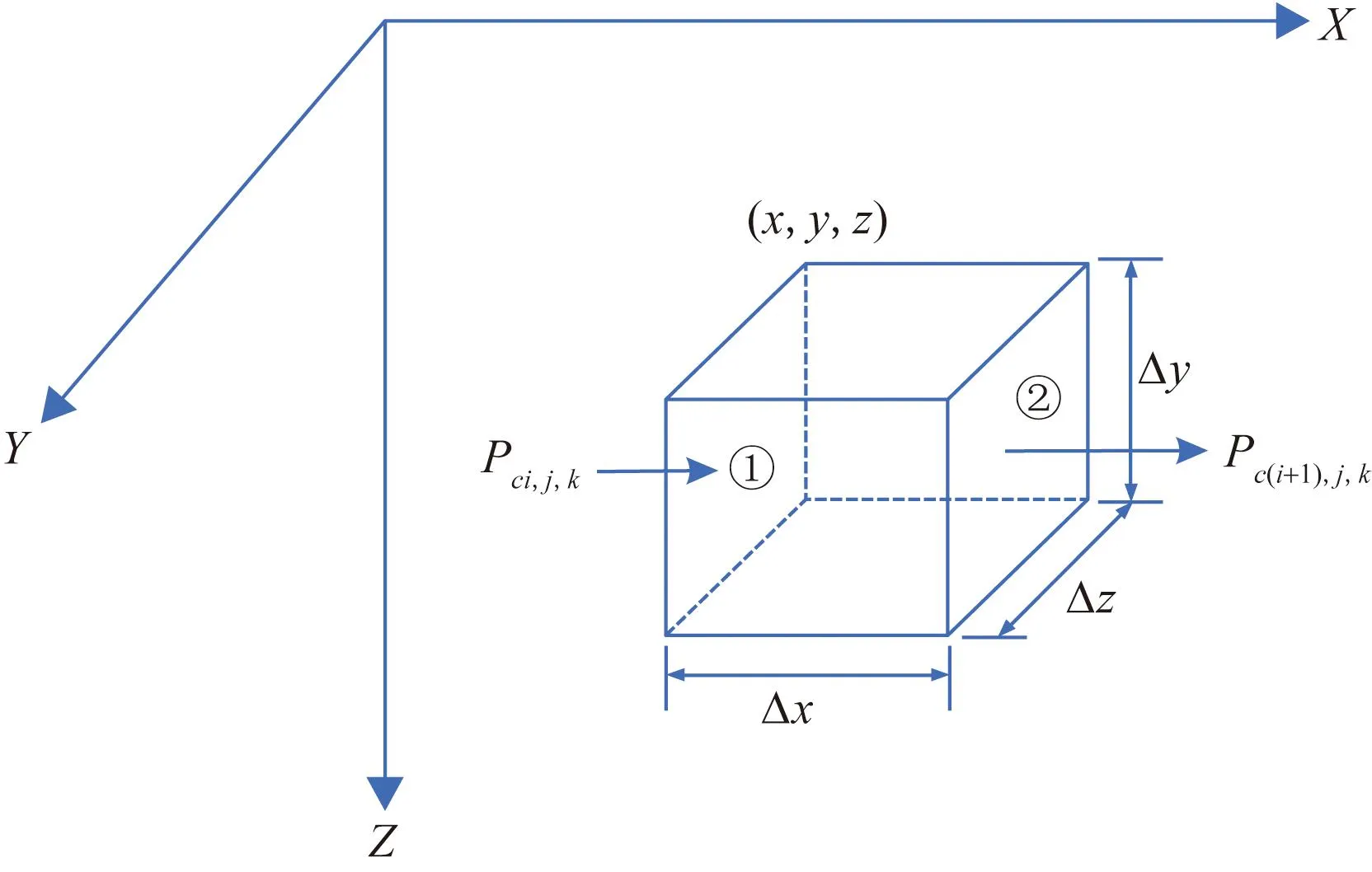
图5 X方向网格面所受毛管力示意图Fig.5 Schematic diagram of capillary force acting on grid surface in X direction

(4)

同理,Y方向的毛管力梯度可以表示为

(5)

Z方向的毛管力梯度可以表示为

(6)

1.2.3 储层网格内流体重力表征方法

油水渗流过程中,流体会受到重力作用。重力梯度的方向竖直向下,其大小由纵向上相邻点处的流体密度决定。在本文数值模型中,根据某一网格面与其纵向上相邻网格面处的流体密度,可以求取重力梯度的大小,实现重力分布的数学描述。位置为(x,y,z)的单元尺寸表示为 Δx、Δy、Δz,则网格流体的重力可以表示为

(7)

1.3 储层内流体渗流连续性表征

在水驱油藏中,存在油水两相渗流。由于油水的黏度、比重和润湿性等存在差异,导致两者在储层中受力、渗流速度和渗流方向也存在差异,使油水两相存在相对流动。对其中一相来讲,另一相可以看成是地层骨架的增加,使渗流孔隙缩小,渗流阻力增大,渗透率变小,油水两相流体渗透率之和小于单相流体在储层中流动的渗透率,但是储层孔隙体积基本不变,油水两相渗流必须满足连续性方程。

油水两相渗流的运动方程分别为

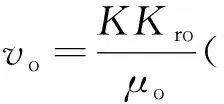
(8)

式(8)中:vo为油相的渗流速度,m/d;K为岩石的渗透率,μm2;Kro为油相的相对渗透率,D;μo为油相的黏度,cp;po为油相压力,MPa;g为重力加速度,m/s2;ρo为油相密度,kg/m3;D为深度,m。

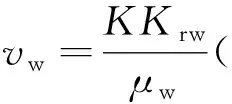
(9)

式(9)中:vw为水相的渗流速度,m/d;Krw为水相的相对渗透率,D;μw为水相的黏度,cp;pw为水相压力,MPa;ρw为水相密度,kg/m3。

油水两相渗流连续性方程为

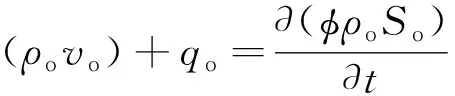
(10)

式(10)中:qo为阶段产油量,104t/a;φ为孔隙度,frac;ρo为油相的密度,kg/m3;So为油相的饱和度,%;t为时间,s。

10-苯基-6,7,8,10-四氢化环戊基并[b]吡咯并[3,2-f]喹啉-9(3H)-酮·DMF的合成和晶体结构

(11)

式(11)中:qw为阶段产水量,104t/a;ρw为水相的密度,kg/m3;Sw为水相的饱和度,%。

2 有无毛管力条件下模型层内作用力分布演化对比

2.1 储层网格选取

如图6所示,基于上述正韵律正方形储层模型沿注水井和采油井对角线的纵向剖面,分别截取低渗层中心和高低渗层交界处的两排网格,应用上述模型网格内流体受力定量表征方法,分别计算各网格内流体在有毛管力影响和无毛管力影响条件下在纵向及横向所受合力的大小,绘制出压力分布图,进行对比。鉴于所选取均为水平网格,网格间重力无变化,在分析时不考虑重力影响,即各网格设置相同的顶部深度。

图6 储层网格选取位置示意图Fig.6 Schematic diagram of selected location of reservoir grid

2.2 有无毛管力情况下单元格受力特征对比

2.2.1 低渗层单元格受力特征

取图6中低渗层中心线处网格,基于表1所示模型参数,应用上文所述储层网格内流体受力定量表征方法,分别计算产液总体含水率在 20%、80%、90%和95%时单元格各表面受力情况,从而得出单元格在纵向和横向所受合力的大小。各单元格在纵向上所受合力计算结果如图7所示,在横向上所受合力计算结果如图8所示。按照图4和图5所示坐标系,纵向上作用力为负值表示方向向上,横向上作用力为正值表示方向向左(即指向采油井方向)。

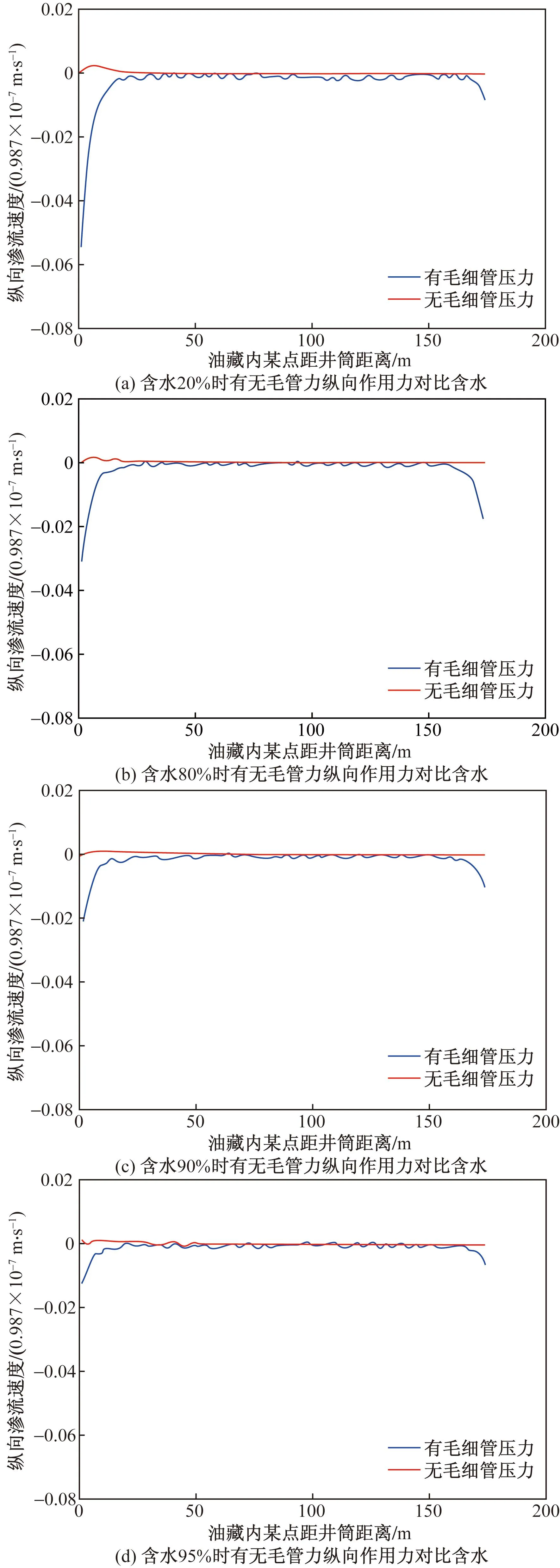
图7 不同含水率有无毛管力纵向作用力对比Fig.7 Different water content with or without capillary force, longitudinal force compared with water content

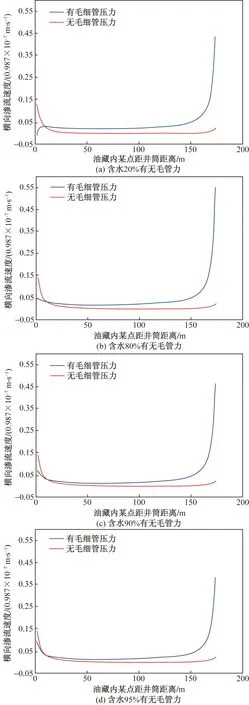
图8 不同含水率状况下有无毛管力横向作用力对比Fig.8 Different water content with or without capillary force, lateral force compared with water content

由图7可以看出,在正韵律低渗透储层中计算流体质点所受纵向作用力时,考虑毛管力影响与未考虑毛管力影响两种情况下计算结果存在较大差别。考虑毛管力影响时,在注水井及采油井附近存在明显的、方向向上的合力,说明该处油藏内流体具有明显向上流动趋势。油藏内含水率越低,毛管力影响越明显,流体向上流动趋势越大。在油藏内含水饱和度逐渐增加的过程中,毛管力影响逐渐减小,流体向上流动趋势减弱。另外,注水井及采油井附近毛管力影响大于油藏中部,这是因为在注水井及采油井附近流体渗流速度大于油藏中部流体渗流速度。而未考虑毛管力影响时,纵向上合力大小基本为0,注入水不具有向上流动趋势[21]。

由图8可以看出,在正韵律低渗透储层中计算流体质点所受横向作用力时,考虑毛管力影响与未考虑毛管力影响两种情况下在采油井附近计算结果存在较大差别,而在注水井附近及油藏中部区域差别不大。在考虑毛管力影响时,在采油井附近存在明显的、方向向上的合力,这是因为在采油井附近含油饱和度高,毛管力影响显著增大,在油藏中部流体渗流速度变慢,毛管力影响也相对较小。随着油藏内含水饱和度增加,在横向上毛管力影响变化不大,主要原因是在油藏中部流体渗流速度变慢,毛管力影响小,即使含水饱和度增加,毛管力影响幅度变化不大,而在水驱作用下,原油向采油井附近聚集,采油井附近含油饱和度仍保持较高水平,因而毛管力影响幅度变化也不大。

2.2.2 高渗层与低渗层交界处单元格受力特征

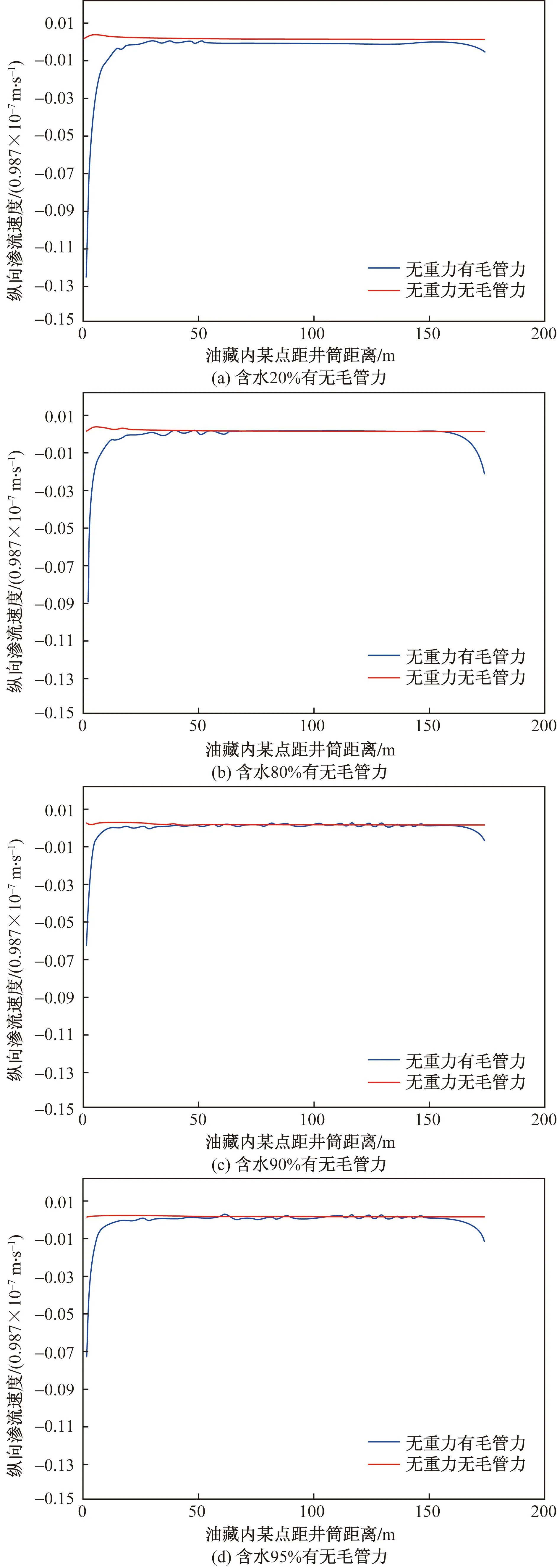
图9 不同含水率状况下有无毛管力纵向渗流速度对比Fig.9 Differentwater content with or without capillary force, longitudinal seepage velocity compared with water content

图10 不同含水率状况下有无毛管力横向渗流速度对比Fig.10 Differentwater content with or without capillary force, lateral seepage velocity compared with water content

从图9可以看出,在图1所示正韵律油藏高渗层与低渗层界面处计算流体质点所受纵向作用力时,考虑毛管力影响与未考虑毛管力影响两种情况下计算结果存在较大差别。考虑毛管力影响时,在注水井附近存在明显的、方向向上的合力,说明在注水井附近流体具有明显向上流动趋势,而在油藏中部及采油井附近毛管力影响较小。而未考虑毛管力影响时,纵向合力基本保持恒定。随着油藏内含水饱和度增加,注水井附近毛管力影响出现小幅减小,但纵向力合力仍然较显著,在油藏中部及采油井附近毛管力影响基本不变。可见,在正韵律油藏水驱开发中,当毛管力的影响增大到一定程度,会出现高渗层向低渗层窜流,导致低渗层底部含水饱和度升高,提高了上部低渗透段驱油效率。

由图10可以看出,在正韵律低渗透储层高渗层与低渗层界面处计算流体质点所受横向作用力时,考虑毛管力影响与未考虑毛管力影响两种情况下,在采油井附近计算结果存在较大差别,而在注水井附近及油藏中部区域差别不大。主要原因是注水井附近含油饱和度低,毛管力影响小,在油藏中部区域渗流速度慢,毛管力影响小亦不明显,而在采油井附近含油饱和度高且流速度快,因而毛管力影响显著。

2.3 纵向渗流速度计算

取图6中低渗层中心线处剖面,选择距注水井井口水平距离16.25 m、垂直距离906.75 m的正方体单元格,单元格边长0.5 m,其他数模参数如表2所示。应用上文所述储层网格内流体受力表征方法,计算单元格内流体纵向渗流速度。

表2 单元格数值模拟参数表Table 2 Cell numerical simulation parameter table

油藏压力梯度对单元格内水相流体纵向渗流速度的贡献为

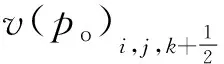
(12)

毛管力梯度对单元格内水相流体纵向渗流速度的贡献为

(13)

重力对单元格内水相流体纵向渗流速度的贡献为

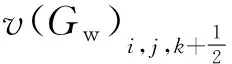
(14)

由此可得,单元格内水相纵向总的渗流速度为

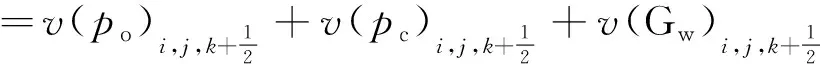
(15)

3 水驱特征模拟

基于上述分析,应用数模软件计算图1所示模型在水驱开发过程中各单元格所受的纵向力和横向力,单元格所受合力的大小和方向反映了单元格内流体的流动趋势,依据式运动方程式(8)、式(9)和连续性方程式(10)、式(11),可以计算出在任意时刻模型内各单元格含水率状况,提取模型纵向剖面,可以观察到注入水在该剖面的主流线特征。为了观察毛管力对注入水主流线剖面的影响,在模型数值设置时将所有网格顶深设置为同一个值,即不考虑重力的影响,然后分别计算无毛管力影响和有毛管力影响时的注入水主流线剖面。

3.1 无毛管力影响时的注入水主流线剖面

提取图1中沿注水井和采油井对角线的纵向剖面,利用上面提到的计算方法,分别计算每个网格的水平渗流速度与纵向渗流速度的数值,导入Tecplot 360可视化处理软件,即可绘制油藏内渗流速度场图。图11分别是综合含水率为20%、80%和95%时,未考虑毛管力影响时该剖面内注入水渗流速度场特征[22]。

图11 不同含水率下正韵律油藏无毛管力影响时注入水主流线剖面Fig.11 Profile of water mainline when capillary force is not affected by capillary force in positive rhythm reservoirwith different water content

由图11可以看出,模型中低渗透及高渗透储层段在无毛管力影响时,注入水大部分进入下部高渗透储层,对高渗透储层内原油进行了有效的驱替,相比高渗层,低渗层水驱前缘突进速度较慢,至产液含水率达到95%时,上部低渗透储层仍具有较高的含油饱和度[23];在匀质的高渗透层段和低渗透层段内,注入水驱油剖面呈现明显活塞驱替形态,在高低渗透层界面处不存在注入水从高渗透层段向低渗透层段渗流现象;在注水井附近渗流速度最大,随着渗流面积增大,渗流速度逐渐减小,越过注水井与采油井连线中点后,渗流速度又逐渐增大[24]。

3.2 有毛管力影响时的注入水主流线剖面

仍取图1中沿注水井和采油井对角线的纵向剖面,考虑毛管力的影响,综合含水率分别为20%、80%和95%时注入水在该剖面内的渗流速度场特征如图12所示。

图12 不同含水率下正韵律油藏有毛管力影响时注入水主流线剖面Fig.12 Positive rhythm reservoir injected water mainline profile when capillary force is affected with different water content

由图12可以看出,在有毛管力影响且到达一定程度时,由于在注水井附近的高低渗透层段界面处存在方向向上的纵向渗流速度,在低渗透层段底部注水剖面出现“舌进”现象[25];随着含水率的上升,低渗层内水驱趋向均衡,开发效果要好于高渗层;当产液含水率达到95%后,此时剩余油主要分布在下部高渗透层段,而非上部低渗透层段[26]。