考虑中间主应力与渗流作用的巷道稳定理论解

刘宇奋, 荣传新*, 王彬, 王松青, 牛宾, 杨明, 黎明镜

(1.安徽理工大学土木建筑学院, 淮南 232001; 2.中煤第三建设(集团)有限责任公司市政工程分公司, 合肥 230000)

煤炭作为中国的主要能源和工业物资,关系到社会发展的稳定,因此煤炭供应的安全问题也是中国能源安全中重要的一环。然而煤炭开采过程中,巷道(隧道)往往穿越地下水充沛的地层,工作面稍有扰动便导致巷道突水事件发生,造成重大损失[1]。在地下工程施工过程中,富水地层的巷道开挖使岩体应力重分布,引起巷道周边围岩塑性变形和损伤,由于岩石的多孔多相材料特征与软化特性使得在复杂地应力场和渗流场下原生裂隙扩展、充水,固、液相之间相互作用即流固耦合作用[2],该作用亦是突水事件重要原因之一。

为了探清地下水渗流与岩石损伤对圆形巷道围岩稳定性的影响,中外学者在理论方面进行了广泛的研究。最开始由Fenner[3]基于理想弹塑性介质提出的Fenner公式,随后Kastner[4]修正为Kastner公式,给出了一种巷道围岩应力和变形的弹塑性分析方法,奠定了圆形隧洞基本计算理论的基础;荣传新等[5]考虑岩石的损伤特性,采用Bui弹塑性损伤模型,分析了巷道的力学状态和失稳准则;贾善坡等[6]将塑性损伤演化与渗流相耦合并通过Mohr-Coulomb破坏准则分析岩石损伤演化机制,再在大型有限元软件Abaqus平台进行了2次开发,建立了相应的有限元损伤数值分析模型并应用于实际工程中,结果良好;Alkan[7]通过统计学和体视学方法评估岩样的微裂缝性质并对微裂缝孔径进行半经验估计,再利用立方定律对全连通渗透率进行建模,将该模型与渗流模型耦合,建立了一种新的渗流模型-逾渗模型,用于预测开挖损伤区中扩容引起的渗透性增加,为流固耦合理论的发展提供了新思路;潘继良等[8]针对受渗流影响的深埋圆形巷道提出一种统一形式的屈服方程,并综合探讨强度准则效应、围岩的剪胀特性等方面影响下相关参数的合理选取;高召宁等[9]在考虑渗流作用对岩体应变软化、扩容等方面的影响,推导出承压水作用下巷道围岩的应力和位移解析解。

但这些研究多是基于理想的弹塑性模型且在研究中大多选用Mohr-Coulomb强度理论,抑或未考虑渗透作用。虽然Mohr-Coulomb强度理论形式简洁但其忽略了中间主应力的影响,在计算围岩稳定性时所得出的结果偏于保守,不能真实反映围岩应力变化特征。Sainoki等[10]和许文松等[11]的研究表明,中间主应力是影响Lode参数、黏聚力和内摩擦角的根本因素与围岩的变形、破坏关系密切,在实际工程中,合理考虑中间主应力的区间效应,可以充分释放岩石材料的强度,减少隧道工程在支护方面的投资,这是对岩石中间主应力效应及其应用的重要推动。

由此可见,针对渗流引发的巷道稳定性问题,亟须研究围岩在应力-渗流-损伤耦合效应的情况下的变化特征。基于此,在考虑中间主应力作用的情况下,现基于Drucker-Prager强度理论,对渗流作用下圆形巷道围岩的稳定性进行分析。

1 理论模型

1.1 Drucker-Prager屈服准则

Drucker-Prager屈服准则(以下简称D-P准则)是在米赛斯屈服准则的基础上考虑平均压力推导得出。由于表述简单且数值计算效率很高,在岩土工程领域应用广泛[12]。D-P准则的屈服函数可以表示为

(1)

式(1)中:I1为应变张量第一不变量;J2为应力偏量第二不变量;α和β为物性参数且均为正的常数。

在关联流动法则下推导出平面应变状态下与Mohr-Coulomb准则匹配D-P准则,即M-C内切圆准则。郑楚键等[13]和刘金龙等[14]的研究表明在平面应变条件的关联流动法则下采用M-C内切圆准则,结果比较契合。其α、β的表达式为

(2)

(3)

式中:c、φ为岩土材料的黏聚力及内摩擦角。

根据赵春风等[15]、张小波等[16]和陈梁等[17]的研究,引入中间主应力系数n使D-P准则改写成类似M-C准则的形式进而简化计算。n的表达式为

(4)

式(4)中:σ1、σ2、σ3分别为最大主应力、中间主应力和最小主应力。由于σ1≥σ2≥σ3,故n的取值范围为0≤n≤1。

式(4)可写成σ2=nσ1+(1-n)σ3,将σ2代入I1、J2中,可得

(5)

(6)

将式(5)和式(6)代入式(1)中,可得

(m-nα-α)σ1-(m-nα+2α)σ3-β=0

(7)

σ1=Aσ3+B

(8)

1.2 巷道围岩理想力学模型

为简化计算,可视为平面应变问题。假设巷道整体水平深埋于地下,横截面为圆形,巷道围岩为连续、均质、各向同性介质,忽略计算范围内岩石的自重,考虑到本文应用的隧道工程的埋深,设侧压力系数[18]λ=1。建立如图1所示的巷道模型:巷道半径为r0,塑性损伤区半径为r1,计算区域半径为r2,原岩应力σ0和孔隙水压力P0都是均匀应力场。巷道断面上的切向应力σθ、径向应力σr和巷道轴向应力σz两两正交,且一般σθ最大、σr最小,考虑到应力大小关系得σ1=σθ,σ2=σz,σ3=σr。

图1 理想力学模型Fig.1 Ideal mechanical model

假设巷道围岩物性参数如下:渗透系数为k,有效孔隙率为φ,弹性模量为E,泊松比为μ。

考虑到岩石的破坏特征及损伤后岩石力学强度的损失,采用Bui弹塑性损伤模型,单轴压缩下其应力-应变曲线简化为如图2所示的图形。当岩石未达到抗压强度前处于线弹性状态,忽略抗压强度前岩石的初始损伤;当岩石达到抗压强度后开始进入塑性损伤软化状态,即超过峰值后为线性各向同性损伤演化。巷道围岩屈服前为弹性,屈服后符合D-P准则。

图2 Bui弹塑性损伤模型Fig.2 Bui Elasto-plastic damage model

单轴压缩条件下一维损伤演化方程为

(9)

式(9)中:εs为最大弹性应变。

根据伊留申假设,若将一维扩展到三维,即三向应力情况下的损伤演化方程只需用等效应变代替单轴情况下一维损伤方程中的ε。设三维情况下主应变为ε1、ε2、ε3,则等效应变εe为

(10)

代替后得三维情况下的损伤演化方程为

(11)

式(11)中:G为降模量;σs为岩石吸水后的单轴抗压强度。

2 巷道围岩稳定性的理论解

2.1 物性方向的确定与孔隙水压分布规律

应力方向以受压为正,因此应变以减小为正,位移以坐标轴负方向为正。

假设渗流以径向渗流为主,忽略计算区域内水的自重和渗流体积力中的浮力,渗流过程符合达西定律。在地层中孔隙水和岩石骨架共同承担地应力的作用,如图3所示。

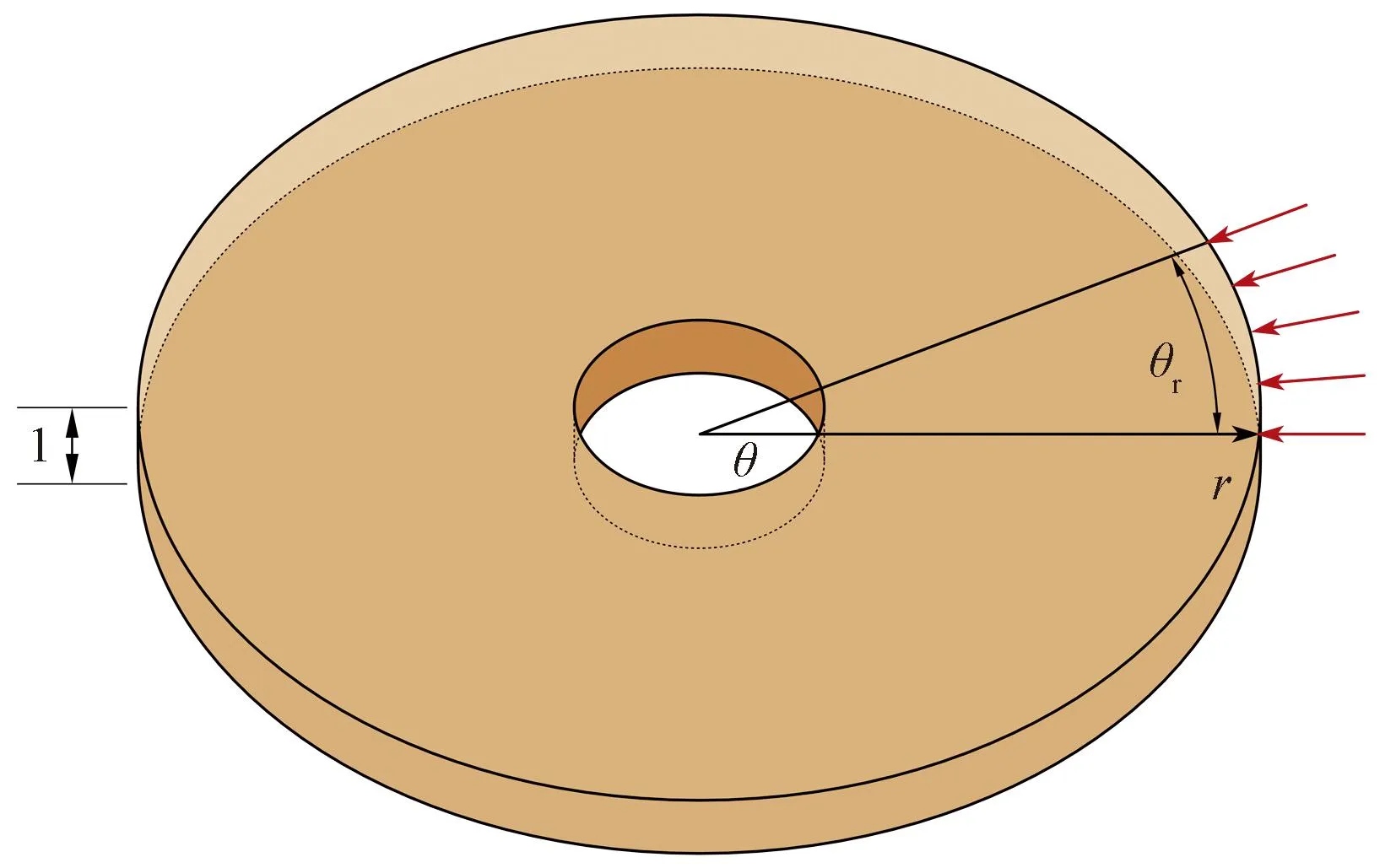
图3 孔隙水压分布图Fig.3 Pore water pressure distribution

由达西定律q=[kδ(P2-P1)]/ηL,其中δ为水流过的截面积,η为水的黏度,L为水流过的距离,则水流过半径为r的单位长度空心柱体的流量为

(12)

由边界条件P|r=r0=0、P|r=r2=P0得孔隙水压力沿半径方向的分布规律为

(13)

2.2 基本方程

平衡方程为

(14)

几何方程为

(15)

式(15)中:εr为径向正应变;εθ为环向正应变;γrθ为切应变;u为径向位移。

弹性区的本构关系(平面应变问题)为

(16)

由式(8)可得塑性损伤区的本构关系为

σ′θ=Aσ′r+B

(17)

式(17)中:σ′θ为塑性区切向应力;σ′r为塑性区径向应力。

边界条件为

(18)

2.3 巷道围岩弹性区应力

将式(13)、式(15)和式(16)代入式(14)得一欧拉方程,解得

(19)

通过边界条件式(18)确定积分常数并解得弹性区的应力分布为

(20)

(21)

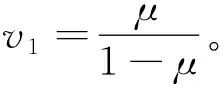
2.4 巷道围岩塑性损伤区应力

假设围岩为各向同性损伤,则

(22)

将式(22)代入式(17)中,得

σθ=Aσr+(1-D)B

(23)

(24)

由式(13)、式(14)、式(23)和式(24),通过积分,结合边界条件式(18)解非齐次线性微分方程,得巷道围岩塑性区的径向应力分布为

(25)

2.5 孔隙水压力关于塑性区损伤半径的关系式

巷道围岩塑性损伤区一侧由式(25)得

(26)

巷道围岩弹性区一侧也满足式(23)。由式(24)得D=0。将之与式(20)和式(21)代入式(23)得

(27)

(28)

根据极值点失稳理论(第二类失稳):因结构存在初始缺陷,结构在荷载作用下保持平衡,随着荷载的增加其变形不断增加,结构保持平衡状态,当荷载增加到极限荷载时,即使荷载不再增加,结构将丧失稳定性。对于巷道围岩,掘进前岩体在地应力作用下处于初始稳定状态,掘进后巷道围岩部分应力重新分布,变相为外荷载增加,塑性区失衡,在可变塑性区内存在某个极值点。故巷道围岩失稳判别准则为:dP0/dr1=0。

3 工程案例分析

工程案例选择位于陕西省榆林市小纪汗乡的可可盖井田主副斜井,按倾角5.6°下山施工,斜长5 304 m(不包括煤巷段)。其中,设计明槽开挖段264 m,掘进机施工法段4 953 m。主要承担矿井提煤、进风任务,兼做安全出口。

主副斜井掘进断面直径7 130 mm,采用锚网索喷支护;自上而下穿过第四系风积沙和黄土(厚约45 m)、白垩纪下统洛河组(厚约221.4 m)、侏罗系中统安定组(厚约62.7 m)、侏罗系中统直罗组(厚约135.8 m);其中洛河组是主要含水层。施工时,每500 m斜长设置临时水仓一个,如果涌水较大,可根据实际需要增设临时水仓。

白垩纪下统洛河组岩性单一,主要为中～细粒弱胶结砂岩(图4),质地疏松,孔隙度较大,地下水的渗流条件较好,适合作为本次研究分析的对象。

图4 洛河组弱胶结砂岩Fig.4 Weakly cemented sandstone of the Luohe Formation

根据实际工况可知巷道半径r0=3.5 m,计算半径取r2=20 m。取地下175 m左右的泥岩,原岩应力测试结果如表1所示。

表1 地下175 m左右的白垩纪下统洛河组泥岩相关参数Table 1 Parameters of 175 m underground Cretaceous Lower Luohe Formation sandstone

采用D-P准则,中间主应力系数n取0.8时,孔隙水压力P0随塑性区半径r1的变化如图5所示,并于MC准则做对比。

图5 不同准则下孔隙水压力P0与塑性区半径r1的示意图Fig.5 Diagram of pore water pressure P0 and plastic zone radius r1 under different criteria

根据计算绘出的孔隙水压力P0与塑性损伤区半径r1的关系曲线可知,图5中的极值点即为巷道围岩稳定的临界点。因此当中间主应力系数n=0.8时临界水压力为10.0 MPa,而采用MC准则时临界水压力为8.4 MPa。巷道围岩中的孔隙水压力接近临界水压时,巷道围岩处于非稳定平衡状态,在此情况下巷道围岩如受到轻微的扰动即将发生突水事故。因此需要加强支护等方法提高塑性损伤区承载力,抑制塑性区的发展。

取中间主应力系数n对应的孔隙水压力极值点绘制成临界水压力Pe的变化图并与基于MC准则的临界水压做对比,结果如图6所示。

图6 中间主应力系数n与临界水压力Pe的关系曲线图Fig.6 Curves of intermediate principal stress coefficient n and critical water pressure Pe

事实上,临界水压力为负值有悖于实际。一方面,本文研究中岩石的抗剪强度参数均由常规三轴压缩试验得出,而Hajiabdolmajid等[19]和栾茂田等[20]指出,现场应力条件不同于土工三轴试验中轴对称应力条件,平面应变状态下采用三轴试验的抗剪强度参数偏于保守。另一方面,按照刘金龙等[21]的研究:根据对参数α的区间有效性的分析,中主应力系数n既有对强度指标的放大效应又有在定义域上区间效应即某区间段无解,该结论与本文结果相一致。综上所述,中间主应力系数应根据实际工程去选择。

在去除无物理意义的点后,图6表明,采用D-P准则时中间主应力系数与临界水压力的关系曲线表现为类抛物线形式。当n=0.35时临界水压力最小为0.08 MPa,n=0.35～0.8时临界水压力逐渐增加,在n=0.8时达到最大值10.0 MPa,n=0.8～1时临界水压力逐渐减小,当n=1时临界水压力为7.34 MPa。同时表明采用MC准则计算结果较大,意味着在考虑中间主应力时D-P准则与之相比更能反映岩石多向受载作用下力学性能。

可可盖井田主斜井采用本文理论解析解,在过洛河组段支护参数优化为:锚杆采用HRB400钢筋,Φ22 mm×2 800 mm的高强度螺纹钢锚杆;顶帮部间排距900 mm×900 mm,菱形布置。锚索选用Φ17.8 mm×7 300 mm钢绞线进行支护,有效长度7 050 mm,每排3根,间排距1 800 mm×2 700 mm。工程实践表明,支护方案能够保障洛河组弱胶结砂岩含水层在渗流条件下的围岩稳定。

4 结论

(1)考虑地下水渗流与不同程度的中间主应力对巷道围岩的影响,应用弹塑性损伤力学理论,基于Drucker-Prager屈服准则,推导得出巷道围岩的应力分布规律以及巷道损伤区半径与孔隙水压力之间的关系式。

(2)当巷道围岩中的孔隙水压力接近临界值时,巷道围岩处于非稳定平衡状态,在此情况下如受到轻微的扰动,则巷道围岩因失稳而坍塌,从而发生突水事故,因此需要安装衬砌等方法提高塑性损伤区承载力,有效抑制塑性区的发展,使其减少临界水压的到来。

(3)分析表明,中间主应力对临界水压力有较大影响,采用D-P准则时中间主应力系数与临界水压力的关系曲线表现为类抛物线形式。在n=0.8时达到最大值10.0 MPa,与MC准则做对比,其临界水压力计算结果较小为8.4 MPa。意味着在考虑中间主应力时D-P准则与MC准则相比更能反映岩石多向受载作用下力学性能,应用于实际工程中效果良好。