混沌线程池与GPU优化的批量图像加密算法
2024-01-05潘明华王一涵谷盛民孙绍华
潘明华, 王一涵, 谷盛民, 孙绍华
(1.桂林电子科技大学广西密码学与信息安全重点实验室, 桂林 543000; 2.桂林电子科技大学人工智能学院, 桂林 543000)
数字图像是一种重要的信息获取方式。随着互联网的发展,恶意第三方攻击可能会使得图像信息遭受到威胁,尤其可能涉及个人、企业、国家的隐私和财产甚至生存的安全。数字图像加密是保护图像信息安全的重要途径之一,大量的学者和企业投入了相关加密算法的研究。随着图像采集设备的迭代更新、大数据的发展以及人们日趋复杂的需求,大规模数字图像的传输引起了广泛关注。在保证传输速率的同时,如何对大批量图像进行加密传输是一个亟需解决的问题。
混沌系统具有对起始参数值敏感、随机性强、可无限遍历等特点,其行为表现为不确定性、不可重复、不可预测。因此,基于混沌系统的图像加密技术成为数字图像加密领域的常用方法之一[1-3]。例如,Chai等[4]提出基于DNA序列和混沌系统进行图像加密;Kumar等[5]提出结合二维Logistic映射和Lorenz-Rossler混沌系统的图像加密;刘思聪等[6]提出二维余弦混沌系统,引入指数和高次幂非线性项构造新型混沌映射。最近发展的量子图像领域中,Zhou等[7]提出了利用Lorenz系统进行量子图像加密和解密;刘瀚扬等[8]提出利用量子随机行走和多维混沌对图像加密。
图形处理器(graphics processing unit, GPU)是一种图像和图形相关运算工作的微处理器。GPU提供多个并行计算的基础结构,可以执行海量数据的并行计算;同时,拥有更高的访存速度和更高的浮点运算能力。随着GPU性能的不断提高,GPU已不仅仅运用于图像、图形处理[9-10],也广泛被运用于通用计算中[11-15]。例如,郭良琛等[13]提出利用GPU进行网络功能虚拟化(network function virtualization, NFV)系统架构的设计和性能优化。胡蓉等[14]提出了一种基于GPU的并行Sinkhorn-WMD算法并通过实验展示了其显著的优化性能。丁光耀等[15]提出了面向GPU的模型共享技术,在任务之间共享同一份模型数据,实现了一个支持大规模推理负载的分布式原型系统。
随着采集设备的迭代更新、大数据的发展与日趋复杂的需求,数字图像信息的大规模传输已成为主流。为了保护这些图像信息,需要在传输前进行批量图像的高速加密。针对该需求,现设计一种基于Lorenz混沌的线程池与GPU组合优化批量图像加密算法,为了简单起见,后续简称为组合优化批量图像加密算法(combinatorial optimization of batch image encryption algorithm,CBIE)。为了检验算法性能,将在抵抗暴力攻击、差分攻击以及统计攻击等方面对算法的安全性进行分析,同时对比组合优化前后的图像读取和加解密处理的效率进行分析。
1 相关技术
1.1 Lorenz混沌系统
Lorenz混沌系统是最早发现的呈现混沌运动的耗散系统,其动力学方程为
(1)
式(1)中:α、β、ρ为3个正实数,代表Lorenz系统参数。
参数的选择对系统是否进入混沌状态起着重要的作用。一般地,取α=10、β=8/3,将ρ作为变量且当ρ>24.74时,Lorenz系统进入混沌状态。当ρ=28时,Lorenz系统进入理论最佳混沌状态;此时只要给系统x、y、z设定一个初值,对t进行指定步长的迭代就能不断生成关于x′、y′、z′的混沌序列。
1.2 加密图像的安全性评估指标
安全性是评估一幅加密图像效果的关键指标。主要评估加密后的图像在受到异常攻击时的对抗能力。下面介绍抵抗差分攻击和统计攻击中常见的指标[1]。
1.2.1 差分攻击
差分攻击是指攻击者对原始明文图像I0进行细微的改变得到改变后的图像I1,利用加密算法生成相同的秘钥,对图像I0和I1加密得到密文图像C0和C1,找出原始两者之间的关系,利用这种关系找到攻击图像加密方案的线索,从而对密文图像进行破解。抗差分攻击性能依赖于对明文的敏感性,对于数字图像,灵敏度的评估通常采用两个参数:像素数变化率(number of pixels change rate, NPCR)和统一平均变化强度(unified average changing intensity,UACI)。NPCR和UACI分别表示两幅密文图像之间的变化像素数和平均变化强度数,它们的定义分别为
(2)
(3)
式中:M和N分别为两幅随机图像的宽度和高度;D(i,j)为两幅图像在二维坐标(i,j)上的像素值距离;C0(i,j)和C1(i,j)分别为原图像和改变后图像在坐标点(i,j)的像素值。如果改变图像的某个像素值引起密文图像的大改变, 则说明该算法抵御差分攻击能力较强。
1.2.2 统计攻击
一般而言,一幅数字图像的像素信息分布是呈规律化的。利用统计规律的攻击方案称为统计攻击,是最常见的数字图像攻击方法之一。攻击者对截获的密文图像进行统计分析,总结出其统计规律,并与明文的统计规律进行比较,从中提取明文图像和密文图像之间的变换关系,以达到攻击加密方案的目的。常用的数字图像统计学分析法包括直方图分析、像素相关性分析、信息熵分析等。
(1)直方图分析。数字图像的直方图是图像在强度的分布,即像素取值分布图,通常取值为[0, 255]。直方图能够直观地反映该图像像素的分布情况。对于一幅RGB彩色图像,可以通过观察其在R、G、B三通过像素的分布情况。为了抵抗统计攻击,图像加密后的直方图分布应该完全不同于明文图像的直方图,并且是均匀的。
(2)相关性分析。相关性分析是指对具备相关性的变量元素进行分析,从而衡量变量之间的相关密切程度。当图像相邻像素之间存在着很高的相关性时,一个像素往往会泄露其周边像素的信息,攻击者可以利用此特性推理出下一个像素的灰度值,从而实现对整个明文图像的恢复。因此,密文图像的相关性必须降低,以避免统计攻击。对一幅总像素为N的图像,其相关性计算公式为
(4)
(5)
(6)
(7)

根据式(4)可知相关性Rxy∈[-1,1],1表示两者完全线性相关,-1表示两个变量完全负相关,0表示两个变量不相关。因此,密文图像相关性越接近于0,则说明加密算法越好。
(3)信息熵分析。信息熵是度量随机性的一个重要参考指标,可以用来衡量图像的随机性,反馈图像内容的混乱程度。信息熵越大则图像混乱的程度就越大,越能抵抗统计攻击。信息熵计算公式为
(8)
式(8)中:xi为像素值;p(xi)为对应像素值出现的概率。
根据信息论最大熵理论,各灰度值等概率时获得最大熵。因此,对于灰度级数为L的图像,加密后的理想熵值为log2L。
2 组合优化批量图像加密算法(CBIE算法)
CBIE算法基于Lorenz混沌和镜像变换进行加密,结合线程池与GPU组合优化实现批量图像加密。整个算法框架如图1所示,主要包括基于线程池的批量图像读取、批量图像变换、批量图像分块及打包、基于Lorenz系统的批量混沌序列生成和基于GPU并行优化的批量加密等模块。
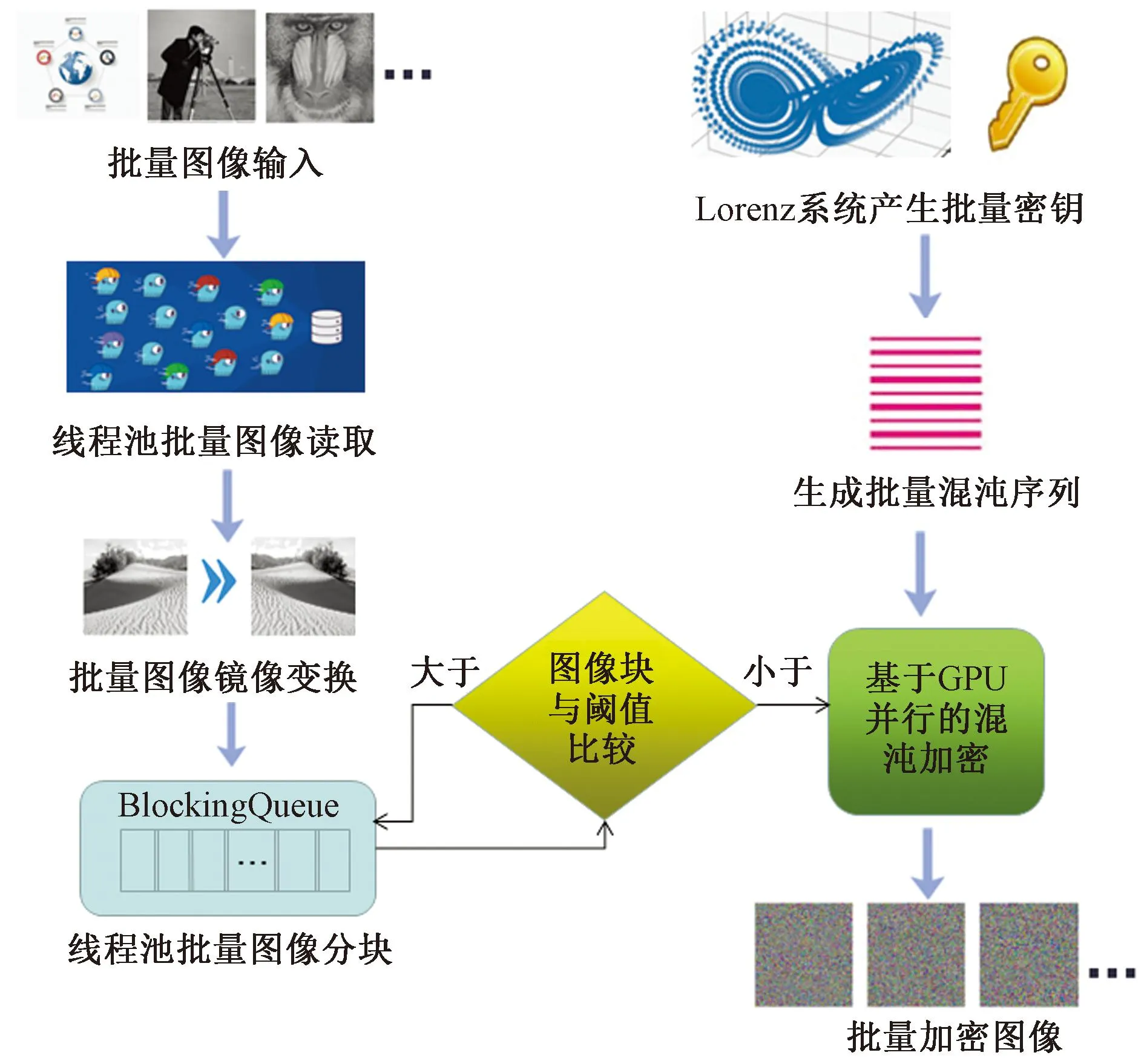
图1 组合优化批量图像加密框架Fig.1 The framework of combinatorial optimization of batch image encryption
2.1 基于线程池的批量图像读写
为了对批量图像进行加密处理,必须先读取图像。由于数字图像本身像素比较高,批量图像的读写更是耗费大量的时间。对于大批量的图像,每一幅图像都可以看成是独立的任务,可以采用多线程任务来执行。但是线程的创建和销毁也是需要时间消耗的,当批量图像的数目较多时,浪费在线程创建和销毁的总时间也是一个不可小觑的。因此,采取线程池的方式使得多任务同时进行,采取异步输入/输出(Input/Output, I/O)的方法提高系统的读写性能。
利用CPU多核特性,采用线程池结构对读写任务优化,提高算法图像读取的效率。线程池包括任务队列、空闲线程队列和忙碌线程队列。为了减少线程创建与销毁的时间开销,利用线程池对象创建时构造若干个线程,在对象销毁前这些线程可以复用到各类任务上。
线程池的作用是维护一个任务队列,其工作方式是在创建时构造指定的空闲线程队列,若任务队列有任务进入且线程池有空闲线程,则分配一个空闲线程去执行任务队列的任务,直到该任务执行结束之前这个线程都不会处于空闲状态,如此反复直到任务队列里没有任务需要处理。对于所有待处理的图像读写任务全部分配到线程池的任务队列里,此时只要任务队列不空,那么线程池会一直利用空闲线程去处理队列中的任务,直到任务队列为空时整批图像的读写任务完成,从而实现批量数字图像读写性能的优化。
2.2 批量图像镜像变换
为了提高图像加密效果,对用户输入的大批量数字图像进行镜像变换。在这里,采用的是水平镜像变化。考虑大批量的图像处理,为了合理利用线程池,首先对输入的批量图像进行分批。
n=N/t
(9)
式(9)中:n为每批次的图像数量;N为批量图像总数;t为线程池中空闲线程数。
然后,对于每批的图像采用轮循机制异步读取,在读取任务完成后立刻对图像进行水平镜像变换,变换过程为
(10)
式(10)中:x、y和x0、y0为变换前、后的像素坐标;w为图像的宽。
2.3 基于线程池的图像分块
考虑实际的数字图像可能像素尺寸极大,尤其是彩色图像具有3个通道,那么其总像素数据量可能非常庞大的。因此,考虑对尺寸极大的图像进行分块,这样既能降低混沌序列的储存量,也能提高混沌序列的生成速度,同时更是为后续的性能优化提供了可能。
提取经过预处理后的批量图像M(m1,m2,…)进行图像分块及数据打包。分块及打包的过程如图2所示,具体分块的步骤如下。
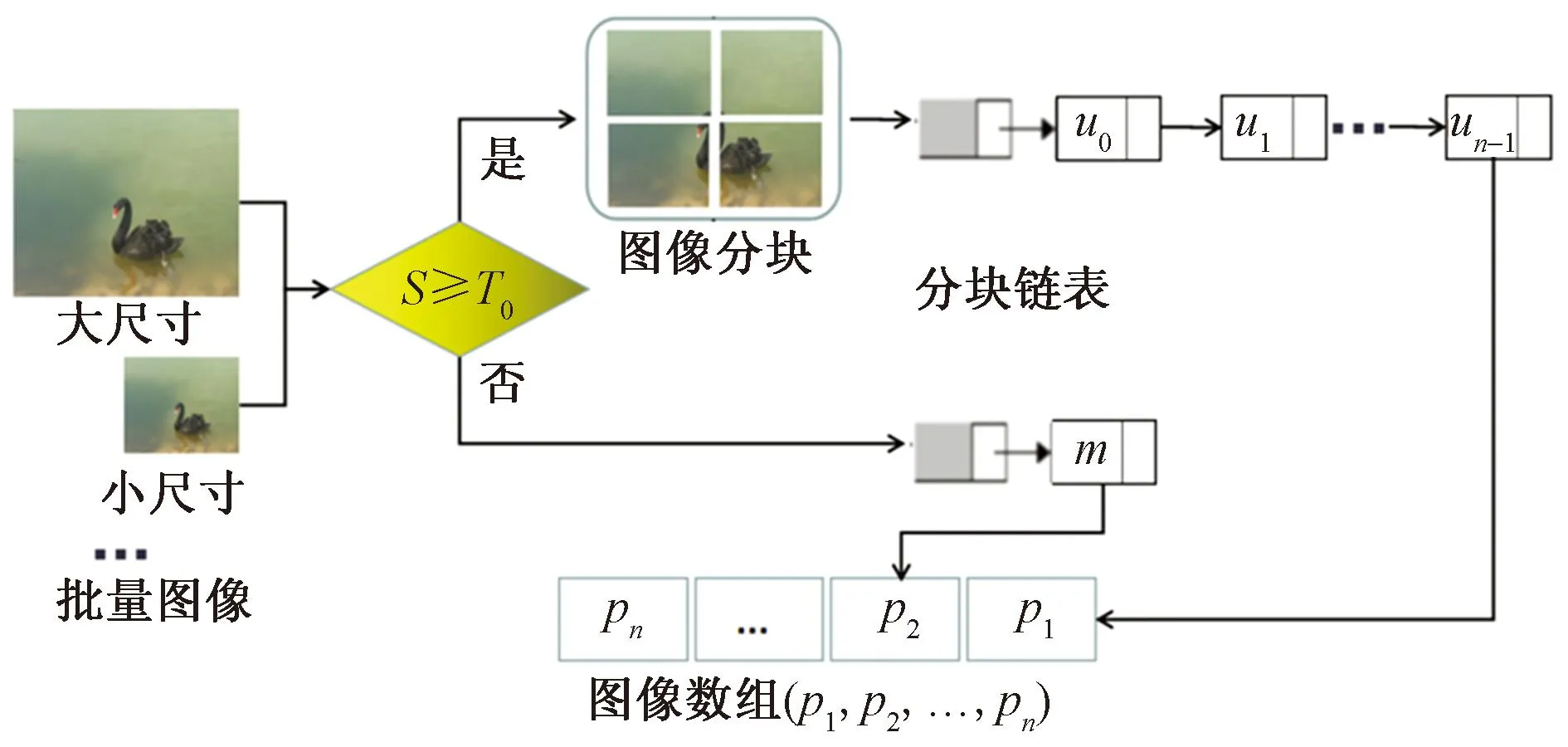
图2 基于线程池的图像分块及打包Fig.2 Image partitioning and packaging based on thread pool
(1)对于每一个图像m,计算图像大小S=wh,其中w和h为图像的高和宽。
(2)分块判断。当S≥T0时进行分块,其中T0是分块阈值。对需要分块的图像,将其拆分成四等块独立的图像,即分块后每一块图像的宽与高值分别为
(11)
式(11)中:j=1,2,3,4。
(3)继续进行分块检测直到满足分块图像尺寸小于阈值T0。对于每一个图像m,最终得到拆分后的像素矩阵m(u0,u1,u2,…)。
(4)图像计算块打包。对于每一个图像m采用Vector
2.4 混沌序列生成
根据1.1节Lorenz动力方程式(1)进行迭代生成混沌序列。设定系统常量,使得Lorenz混沌系统进入最佳的混沌状态,即取α=10,β=8/3,ρ=28。然后,随机选取3个初值,以0.01的步长进行迭代画出生成的混沌序列如图3所示。考虑彩色图像的R、G、B三通道,每一轮的混沌序列迭代生成3组混沌序列。最后,将所有的混沌序列写入TXT文本文件进行储存用于后续的图像加密,至此一轮混沌序列生成完成。

图3 混沌图Fig.3 Chaos figure
2.5 基于GPU并行的混沌加密
除了读写优化之外,批量图像加解密的效率是关键。GPU作为图形处理器,在处理大批量矩阵计算上的效率远远高于CPU,因此引入GPU来加速批量图像的加解密处理过程。利用GPU进行处理时,必须考虑算法执行的顺序以及数据的打包,否则可能导致大量时间被浪费于CPU和GPU的数据通信上。因此,需要进行批量图像加密任务串并行拆分,再进行GPU异步计算加速。
2.5.1 串行下的计算数据打包
为了对批量图像加密进行并行化处理,在利用线程池完成所有图像的镜像变换和分块任务后,需要将原本串行执行的图像像素矩阵与混沌序列做异或运算过程进行计算数据的打包,统一组成一个的矩阵计算数组传给GPU进行大批量的并行异或运算。
考虑一幅图像的矩阵计算数据作为一个计算包,那么批量图像的矩阵运算需要一个数组Vector
2.5.2 GPU异步计算加速
对已打包图像分块数据采用GPU并行计算,具体如下。
(1)构造若干个核函数fun_k(Matu, MatL),其中L是2.4节中基于Lorenz混沌系统产生的混沌序列。
(2)利用GPU编程技术对图像分块处理得到数据进行加密,执行F(fun_k(u0,L0),fun_k(u1,L1), fun_k(u2,L2)…)进行并行批量图像混沌加密,采用的加密方式为
P′i,j=Pi,j⊕Li,j
(12)
式(12)中:P′为密文像素的值;P为明文像素的值。如此,只需将存放对应批量图像的矩阵数组作为计算包数据与混沌序列进行异或即可完成批量的并行计算。
3 算法性能测试与分析
为了对所设计的批量图像算法进行评估,对算法的加密安全性和效率进行性能测试,包括利用直方图、相关性、信息熵等进行分析。
3.1 图像加密安全性测试与分析
3.1.1 暴力攻击
密钥空间是所有可能的生成密钥集合,密钥空间的大小影响着加密系统能否被暴力破解。为了应对暴力枚举攻击当,一个良好的加密系统的密钥空间必须足够大。CBIE的加密密钥采用Lorenz系统生成的随机值作为初始密钥,由随机生成的3个自定义扩展高精度浮点数表示。自定义扩展高精度浮点数由2个bit数组组成,分别代表小数点前的整数部分和小数点后的小数部分表示,其中整数部分由32位bit组成,小数部分由16位bit组成,总共可以代表248种数。因此,枚举所有密钥为
Key=248×248×248=2144
(13)
这即使使用现代高性能计算机,要暴力枚举上述所有密钥需要大约248×1 021年。由此可见,CBIE算法能够抵御任何形式的暴力攻击。
3.1.2 差分攻击
密钥敏感强度测试可以通过修改密钥K中的某一位得到K′,利用两个密钥加密同一张图像得到C0和C1。根据式(2)和式(3),随机选取图像进行测试。式(2)中两幅图像在坐标(i,j)的像素值距离D(i,j)的计算方式有多种,实验计算中采用的计算方式为
(14)
即当两幅图像在坐标(i,j)的像素值不同时,D(i,j)=1;当像素值相同时,D(i,j)=0。在此约定下,NPCR和UACI的理想值分别为NPCR=99.609 4%和UACI= 33.463 5%。通过计算两幅图像的NPCR和UACI,如果计算值越接近理想值,则说明加密算法的密钥敏感度越强,加密算法抗差分攻击能力越强。
经过对100张随机图像进行测试,得到它们在R、G、B三通道上平均的NPCR和UACI实验结果如表1所示,其中平均NPCR在95%~98%,UACI在30%~32%。CBIE算法加密后,像素变化率和像素平均变化强度距理想值略有差距,由此可见CBIE算法有良好的抗差分攻击能力。
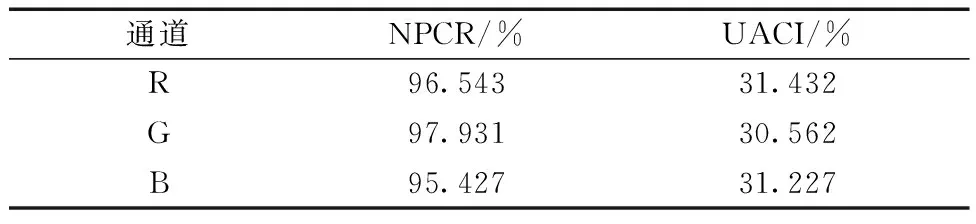
表1 随机100幅图像的NPCR和UACITable 1 NPCR and UACI of 100 images for random
3.1.3 统计攻击
实验中随机选择的数字图像如图4(a)所示,经过CBIE算法加密后得到结果如图4(b)所示,对比两者可以看出加密后的图像已无法分辨原图。为了测试加密后图像对抗统计攻击的能力,对明文和密文图像进行直方图、像素相关性和信息熵分析。

图4 明文图像和其密文图像Fig.4 Plaintext image and its ciphertext image
1)直方图分析
对图4的明文和密文图像分别进行直方图分析,所得结果如图5和图6所示。可见,明文图像的彩色图像直方图和R、G、B三通道像素直方图具有较为明显的特征,而密文图像的各直方图则几乎是均匀的,无明显特征。
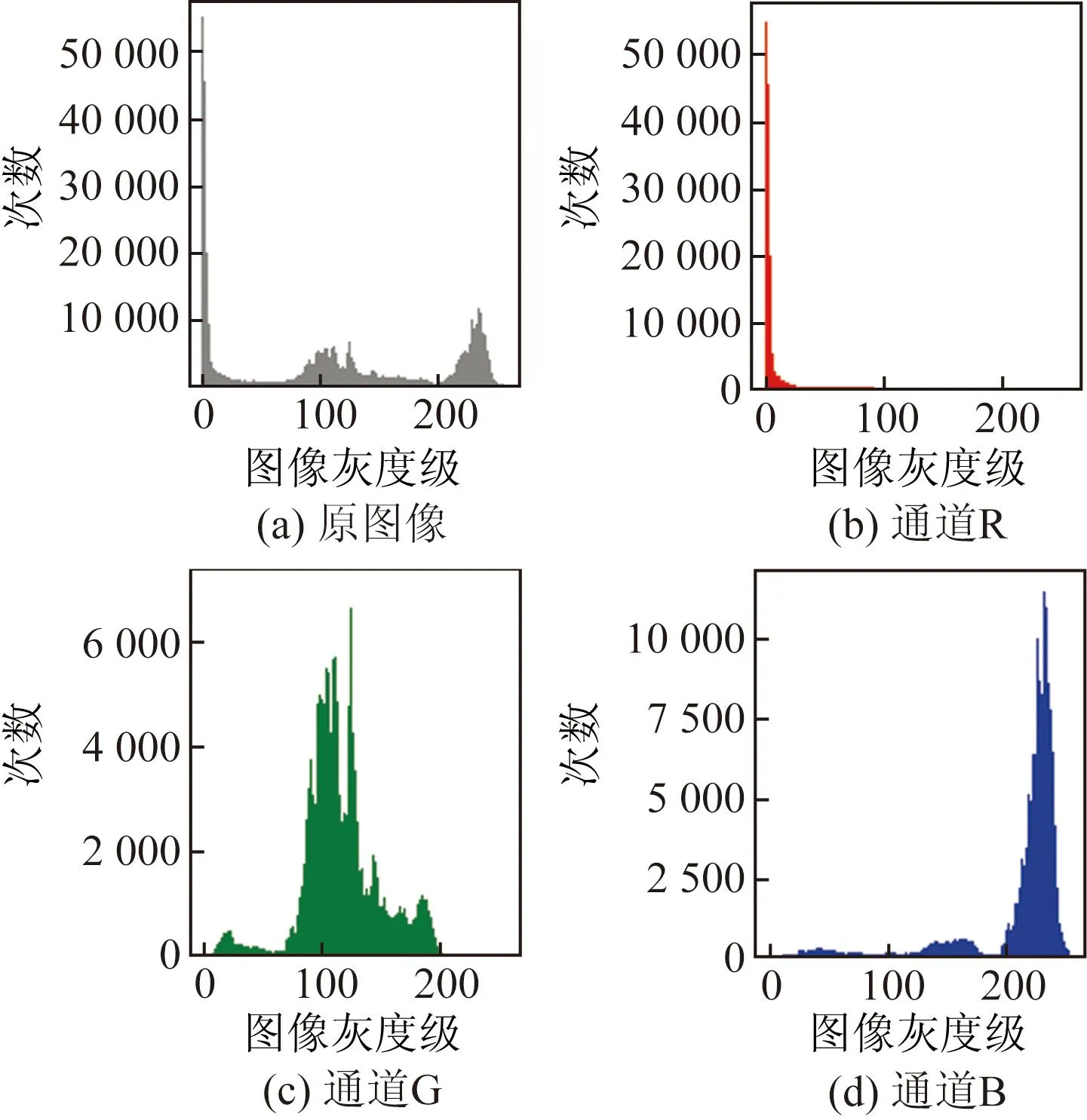
图5 明文图像直方图Fig.5 Histograms of plaintext image

图6 密文图像直方图Fig.6 Histograms of ciphertext image
2)像素相关性分析
根据1.2.2节介绍,利用式(4)~式(7)分别计算图像在水平、垂直和对角线方的相关系数。对彩色图像图4(a)进行加密,然后计算加密前后两幅图像R、G、B三通道的各像素之间的相关性,得到的相关性结果如表2所示,同时以水平方向相关性为例,将其图形化得到结果如图7和图8所示。加密前的明文图像各通道分量的像素相关性均大于0.95,而加密后的密文图像各通道分量的像素相关性均小于0.02。由此可见,加密后的密文图像像素间相关性小,可以有效避免统计攻击。
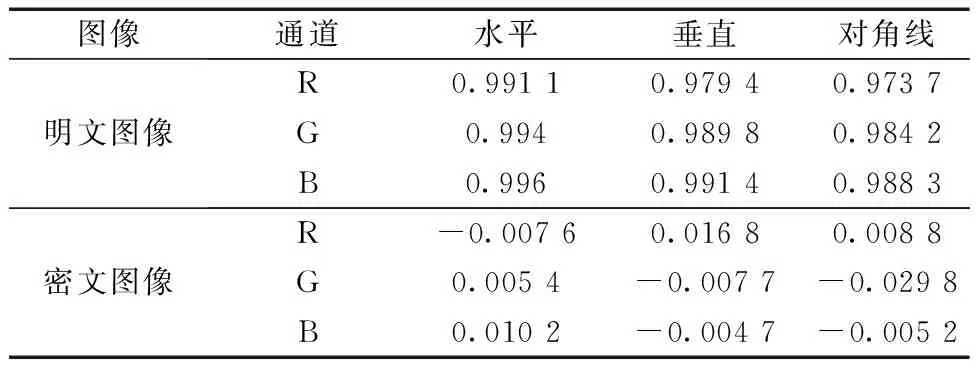
表2 图像及其密文图像的相关性对比Table 2 Relevance comparison between image and its ciphertext

图7 明文图像相关性Fig.7 Relevance of plaintext image
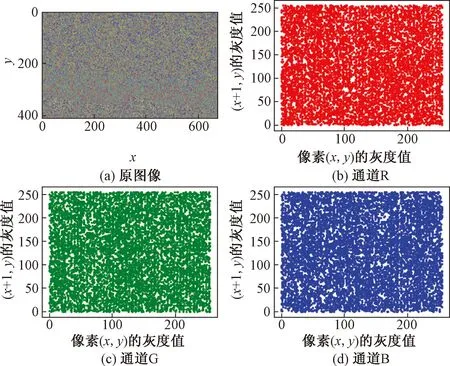
图8 密文图像相关性Fig.8 Relevance of ciphertext image
3)信息熵分析
根据1.2.2节,信息熵越大则图像混乱的程度就越大,对统计攻击的抵抗力就越强。对于彩色图像,R、G、B通道的强度值为0~255,因此加密后的理想熵值为8。根据式(8),对于明文图像和密文图像分别计算R、G、B三通道的信息熵,得到结果如表3所示。对比表3中数据可以看到,明文图像各通道信息熵为4.12~6.81,而加密图像的各信息熵则非常接近最佳抗攻击理论值8。可见加密算法对统计攻击具有较好的抵抗能力。

表3 加密前后的信息熵Table 3 Information entropy before and after encryption
3.1.4 噪声攻击
在现实世界中,图像传输不可避免地会受到各种因素的影响,如噪声。因此图像加密算法必须具有足够的鲁棒性,以抵抗实际场景中的噪声攻击。抗噪声能力是测试加密方案性能的一个重要指标,通过仿真实验对明文图像分别添加不同程度的不同噪声类型,同时对密文图像添加同样的噪声然后再进行解密,进行比较。
最常见的噪声有高斯噪声、椒盐噪声等。对于前述实验中对明文图像4(a)和加密后所得的密文图像4(b)分别添加均值为零,方差为0.0005的高斯噪声和5%的椒盐噪声,同时对加入噪声的密文图像进行解密,所得结果如图9和图10所示。对比图9和图10发现,加密后的密文图像在高斯噪声和椒盐噪声攻击下,解密后的图像也能保存大部分的有效信息;更重要的是加入噪声的密文图像解密后得到的图像比明文图像直接受到噪声干扰的图像更接近原图,这说明CBIE加密算法对噪声干扰具有一定的保护作用。

图9 高斯噪声攻击Fig.9 Gaussian noise attack

图10 椒盐噪声攻击Fig.10 Salt and pepper noise attack
3.2 效率测试与分析
CBIE结合混沌线程池与GPU组合优化批量图像加密。而优化前通常采用单线程进行图像文件的读写,单线程执行整个加密算法流程对数字图像进行批量加密。为了展示组合优化的效率,实验着重测试了从用户提交批量数字图像加密任务之后,将两者在批量图像读取效率和批量图像加密处理效率上进行比较分析。实验系统环境为Window10系统,Python3.7、微软VS2017、基于C/C++的Opencv3.4、CUDA10.0。实验时分别随机选取100、200、400、2 000张不同大小的彩色图像。
3.2.1 批量图像读取效率
通过在代码段打时间戳的方式可以获得执行到指定段的系统时间戳,通过时间戳做差值计算可以获得代码段执行的耗时。算法进程对大批量数字图像文件进行读取耗时统计,结果如表4和图11所示。由此可见,优化前后,读写耗时在达到一定数量后均线性增长。采用组合优化后,读写时间明显下降,用时仅为优化前的1/3左右,读写效率显著提高。

表4 批量图像加密时间Table 4 Batch image reading time
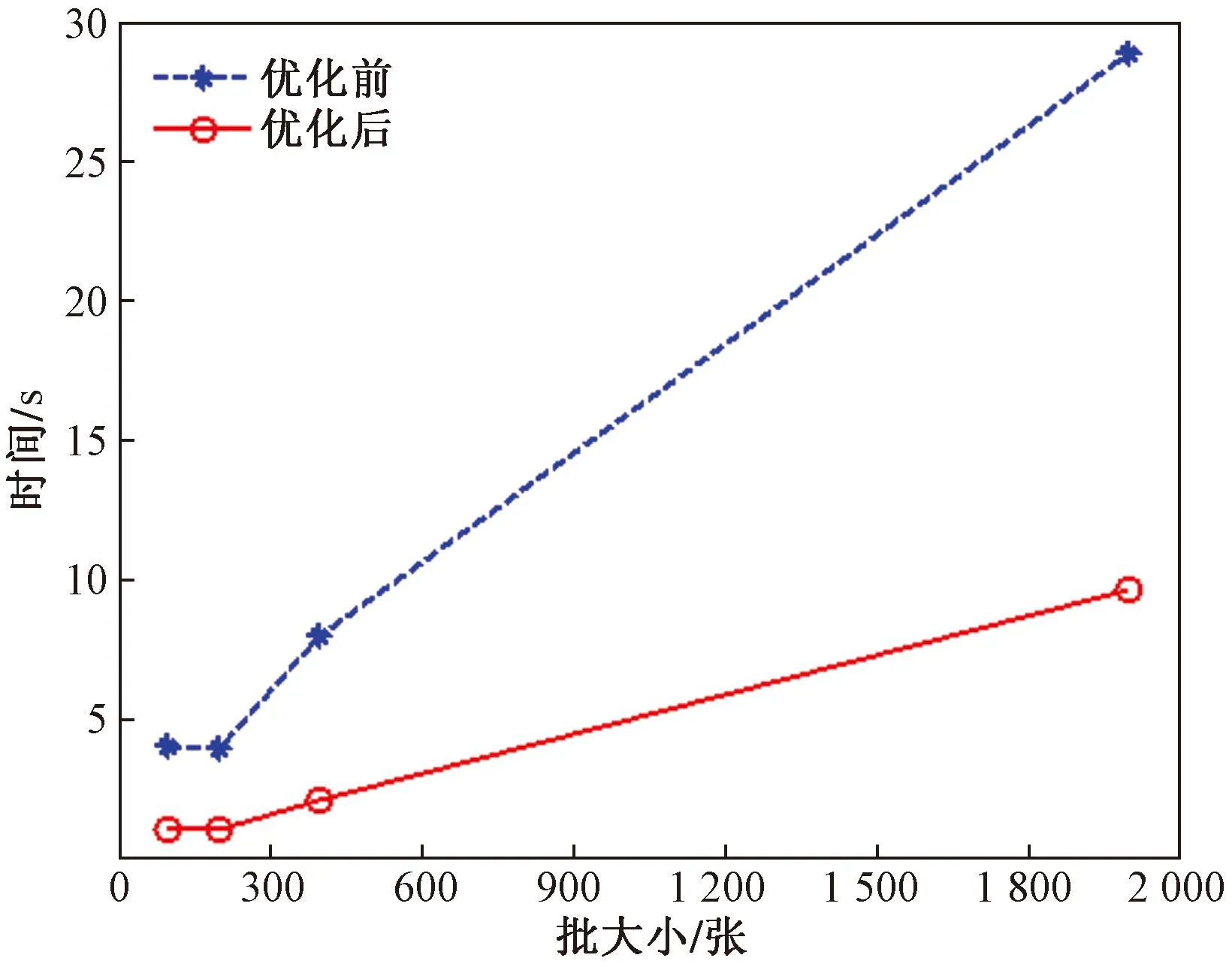
图11 批量图像读写时间Fig.11 Batch image encryption processing time
3.2.2 批量图像加解密处理效率
类似于3.2.1节,对大批量数字图像进行优化前后的批量图像加解密处理的效率进行统计分析,结果如表5和图12所示。由此可见,优化前后,批量加解密处理耗时在达到一定数量后均线性增长。同时可以看到,采用组合优化后,批量图像加解密所需时间显著下降,处理速率对比优化将提升了将近10倍。

表5 批量图像加密时间Table 5 Batch image encryption time

图12 批量图像加密处理时间Fig.12 Batch image encryption processing time
4 结论
为了解决大批量图像读取和加解密碰到的效率问题,提出了一种基于混沌的线程池与GPU组合优化的批量图像加密算法(CBIE算法)。算法对大批量数字图像的读写性能进行了优化,并且对加密算法的过程进行串并行拆分,采用线程池对加密任务进行计算打包,然后利用GPU能够高性能地执行大批量矩阵计算的特点,将打包好后的计算包发送给GPU进行批量异步并行计算。通过分析和实验得到以下结论。
(1)CBIE算法对批量图像加密具有很高安全性。通过密码空间以及利用常见的图像加密算法评价指标进行分析证明了经过CBIE加密后的图像具有对抗暴力攻击、统计攻击以及噪声攻击能力。
(2)CBIE算法显著提高批量图像读写的效率。对不同批大小的批量图像进行读写性能测试和分析,得出CBIE算法比单线程读写速度提升近4倍。
(3)CBIE算法显著提高批量图像加密处理的效率。对不同批大小的批量图像进行加密性能测试和分析,得出CBIE算法对批量图像加解密图像处理速度提升近10倍。
因此,所设计CBIE算法能够满足大数据时代下的大批量图像快速加密的安全性和实时性需求。根据实际需要,本算法可以进一步变换加密算法和改进GPU技术,为更多的应用提供有价值的参考。
