基于倾斜校正和视差估计的遥感影像稠密匹配方法

杨阿华, 杨阿锋, 张强, 常鑫

(1.北京跟踪与通信技术研究所, 北京 100094; 2.杭州电子科技大学通信工程学院, 杭州 310018)

当前,三维物体、场景重建主要有主动和被动两种方式[1-2]。其中,主动方式采用主动传感器设备(如激光雷达)感知物体表面的三维信息,由获取的三维数据经过一系列数据后处理操作,达到重建场景三维结构的目的。此种方式精度高,效率较高,但需要较为昂贵的测量设备,数据获取过程较为繁琐,若想获得具有照片真实感的虚拟三维模型,则需要在采集三维信息的同时采集图像信息,在数据后处理时则涉及点云与图像的配准问题[3-4]。被动方式采用图像传感器获取物体表面的图像信息,根据双目立体视觉原理,由具有一定视差的二维图像对恢复出物体表面的三维(深度)信息。此种方式仅需廉价的普通相机,对目标的形状、尺寸没有特殊要求,数据获取简单、易行,可以生成具有照片真实感的三维模型和场景。但其精度一般较前者要低,且数据后处理过程较为复杂、耗时,对于纹理单一或无纹理的图像区域,则无法获取准确的三维信息。

虽然主动三维扫描在很多应用领域已经成为获取三维信息的重要手段,但基于图像的三维建模仍然是最经济、灵活、易行和广泛使用的方法。

基于图像重建三维物体、场景和地表的关键是同名点稠密匹配,精确、稠密的同名点是获取高精度三维信息的基础。稠密匹配广泛应用于物体精细重建、真实感场景重建和数字表面模型(digital surface model,DSM)及真数字正射影像(true digital ortho map,TDOM)的生成。由于图像色彩偏差、图像形变、图像遮挡、无纹理或弱纹理、重复纹理等问题,导致图像稠密匹配成为一项有挑战的任务。若能实现同名点的准确、稠密和高效匹配,则解决了基于图像的三维重建中精度、效率较低的问题。

传统的图像匹配方法分为基于特征的方法和基于影像相关的方法[5]。基于特征的方法精度和准确率高,但只针对图像中的角点、线、边缘等特征显著区域,因此仅能获取稀疏的匹配点集,且单点计算开销较影像相关方法高很多,一般用来为稠密匹配提供种子点或约束条件[6];基于影像相关的方法由于计算量较大,效率较低,且在纹理单一区域具有自相似性,容易产生误匹配,从而限制了其使用。此外,传统稠密匹配方法或者要求待匹配影像对的基线较短,或者需要多视图约束[7],以提高匹配的可靠性,一定程度限制了其使用。

文献[8]提出了一种基于区域生长的稠密匹配方法,该方法以图像特征点匹配作为初始种子,以零均值归一化互相关系数和双视几何约束作为生长过程中图像对应点的匹配标准,在整幅图像上进行匹配生长,采取视差梯度约束和置信度约束进行匹配优化,获得稠密匹配点。文献[9]将特征匹配结果作为匹配基元,构建 Delaunay 三角网,利用 Delaunay 三角网间的同名三角单元的单应矩阵关系对已有匹配结果进行加密,最后利用最小二乘匹配提高匹配精度,但未达到逐像素的匹配密度。文献[10]同样采用稀疏同名点建立三角网,以描述符与马氏距离作为两种影响因素,通过计算目标点与候选点的匹配得分来确定匹配点,较好地解决了传统算法对于明暗变换和几何变形影像适应性较差的问题,但该方法仅能获取稀疏匹配点凸壳所围区域内的同名点,且匹配效率较低。文献[11]提出了一种结合密度聚类平滑约束与三角网等比例剖分的像对稠密匹配方法,该方法首先基于稀疏同名点构建局部内点集,基于内点集构建三角网,再利用三角网提纯内点集,最后用提纯后的内点集计算稠密匹配点位置,该方法能避免由于局部外点造成仿射变换矩阵估计不准确进而影响稠密匹配准确率的情况,但匹配的精度较低,且对于遮挡引起的误匹配无法消除。文献[12]提出了一种基于局部光照一致性约束的准稠密匹配方法,该方法将已知匹配点作为种子点,根据种子点及其邻域提供的影像约束进行匹配扩散,从而得到种子点邻域内的匹配点,进而实现图像之间的准稠密匹配。文献[13]比较了基于深度学习的影像匹配和传统影像匹配方法,结果表明采用深度学习方法训练的匹配模型泛化迁移能力较差,需要针对特定数据集训练特定模型,对训练数据要求高,且时间开销较大,推广应用优势不明显。因此,传统的影像匹配方法仍然是基于影像的三维重建的主要实现途径。

现提出一种基于倾斜校正和视差估计的遥感影像同名点稠密匹配方法,该方法基于核线影像进行视差估计和搜索匹配,同时充分利用已有信息来优化搜索过程,达到减少计算量、增加匹配约束的效果,最终实现提高匹配效率和降低误匹配的目的。

1 解决方案

遥感相机获取的原始影像不可避免地存在旋转、缩放及透视变形,所以在以匹配点对为中心的左、右影像窗口内,各对应位置的像素并不是完全对准,而是有一定的相对变形,对于近景、宽基线及视角变化较大的摄影情况,变形更为明显,这种变形可以用仿射变换来近似[14]。理想的解决方案是首先求解两个影像窗口的仿射变换参数,再根据该变换参数重采样目标影像块,从而生成相对原始影像块无变形的目标影像块,最后再求原始与无变形影像块间的相关系数,以确定最佳的匹配点。然而上述过程存在2个问题:一是原始与目标影像块间的仿射变换参数难于获取;二是针对每个目标影像窗口的重采样开销巨大,将极大地降低匹配效率。因此这种理想方案不具可操作性。

针对上述2个问题,本文方法通过倾斜校正处理,一次性生成几乎无仿射变形的核线影像对,然后在核线影像上进行稠密匹配,既基本消除了仿射变形,又无需在每次相关匹配时对影像窗口反复进行重采样,避免了重复计算,极大降低了计算量。

本文方法包括5个步骤,分别是:特征匹配、相对定向、核线影像生成、一维灰度相关匹配、最小二乘影像匹配,下面对各步骤所采用的方法进行介绍,其中重点介绍核线影像生成和一维灰度相关匹配。

1.1 特征匹配

Mikolajczyk等[15]对多种特征描述子的性能进行了评价,结果表明尺度不变特征变换(scale invariant feature transform,SIFT)[16]特征描述子具有最强的稳健性,因此,首先采用SIFT特征描述子提取左右图像的特征点,然后进行特征匹配;采用随机抽样一致算法(random sample consensus,RANSAC)[17]算法,根据特征匹配点求解两幅图像的仿射变换关系,并剔除少量误匹配点,最终获得一定数量分布于整个重叠区的可靠同名像点,由左右影像构成一个立体模型。

1.2 相对定向

基于左右影像间的同名点及相机内参数,通过相对定向直接解法[18],再结合光束法平差[19]优化,可以获得立体模型的精确相对定向元素,即确定构成立体模型的两个相机的相对位姿关系,亦即确定右相机坐标系相对于左相机坐标系的旋转矩阵R和平移向量t。

1.3 核线影像生成

为了生成核线影像,首先构造水平核线坐标系(下文简称核线坐标系),然后将左右倾斜影像校正为核线影像。

1.3.1 核线坐标系构建

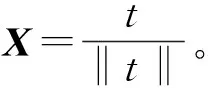
最后,左核线坐标系的Z轴在左倾斜坐标系下的坐标为:Z=XY。

至此,左核线坐标系的三轴向量在左倾斜坐标系下的坐标已经求得,上述过程构造的是一个右手三维直角坐标系。

根据左核线坐标系,构造一个虚拟的左核线相机,该相机的像平面与左核线坐标系的XY平面平行,主光轴与左核线坐标系的Z轴平行,X、Y、Z三轴与左核线坐标系三轴平行。

构造了左核线坐标系后,将任一向量从左倾斜坐标系变换到左核线坐标系的旋转变换矩阵为

(1)

右核线坐标系的三轴与左核线坐标系三轴平行,原点与右倾斜坐标系原点重合,类似的可以构造虚拟右核线相机。将任一向量从右倾斜坐标系变换到右核线坐标系的旋转变换矩阵为

(2)

1.3.2 影像校正

以左相机对应的左影像为例,介绍将倾斜影像校正为核线影像的过程。

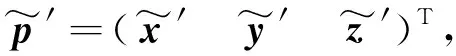
(3)

(4)

根据式(3)和式(4),可将左原始影像中任一像素映射到左核线影像,通过求逆亦可将左核线影像中任一像素映射到左原始影像;类似的,通过将式(4)中的Ml替换为Mr,可得右原始影像与右核线影像的映射关系。

具体校正过程为:首先将c′x、c′y设为0,采用式(3)与式(4)计算原始影像矩形4个顶点像素在核线影像中的坐标,从而得到覆盖核线影像的最小矩形包围盒;将c′x、c′y的值设置为包围盒左下角的x、y坐标(即包围盒的最小x、y坐标),从而使包围盒的左下角与核线影像的左下角重合,同时将核线影像的宽高设置为包围盒的宽高。根据式(3)和式(4),可得核线影像任一像素点在原始影像上的对应点坐标(该坐标为小数值),进而通过灰度重采样从原始影像得到核线影像点的色彩值;遍历核线影像全部像素点,最终生成经过校正的核线影像。图1是位于相邻航线的两幅重叠影像经倾斜校正后的结果。

图1 相邻航线重叠影像倾斜校正结果Fig.1 Tilt correction results of overlapping images of adjacent airlines

1.4 相关匹配

灰度相关匹配基于校正后的核线影像,以保证左、右影像窗口间仅有x方向的较小透视变形。首先以三角形为单元估计左右影像的初始视差;对于左影像的任一待匹配点,根据视差值估计初始匹配点;然后在初始匹配点的邻域内,通过灰度相关匹配搜索最佳匹配点。

1.4.1 视差估计

为了估计核线影像对的初始视差,首先采用式(4),将所有稀疏同名点的原始影像坐标转为核线影像坐标;然后由稀疏点三角构网[20],根据每个三角形3个顶点在x和y方向的核线影像视差,在三角形内插值出核线影像每个像素的x和y视差。如图2所示,p1(x1,y1)、p2(x2,y2)、p3(x3,y3)为三角形的3个顶点,对应的x视差分别为dx1、dx2、dx3,p(x,y)为三角形内一点,p12(x12,y)、p13(x13,y)为第y像素行与三角形两边P1P2、P1P3的交点。首先通过在y方向上线性插值求得点p12、p13的x视差dx12、dx13,即

图2 三角形插值示意图Fig.2 Sketch map of triangle interpolation

(5)

通过将式(5)中的视差换成对应点的x坐标,可求得点p12、p13的x坐标x12、x13。然后由点p12、p13的坐标在x方向上线性插值,即可求得p点的x视差dx,为

(6)

同理可求p点的y视差dy。

值得注意的是,理论上核线影像对中任意位置的y视差是固定的(理论值随校正时采用的像主点列坐标c′y的不同而不同),但实际处理中发现,由于相机畸变系数的误差及畸变的复杂性,生成的核线影像在y方向的视差并不固定,而是在理论值附近的若干个像素范围内波动(此波动范围随畸变大小不同而变化)。因此,此处对y视差也进行插值,使视差的估算精度大大提高,进而提高了匹配的正确率。

1.4.2 相关匹配

采用规范化互相关(normalized cross correlation, NCC)[13]系数来度量两个影像块的相似程度,NCC系数对影像块间的线性亮度变化鲁棒。对于左右影像的两个影像块,其NCC系数ENCC的计算公式为

ENCC=

(7)

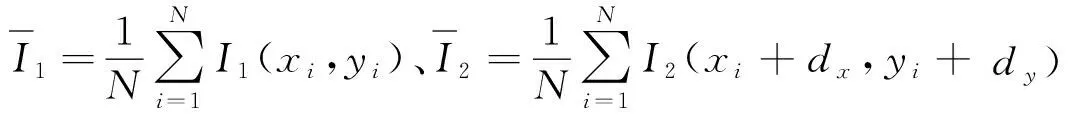
值得注意的是,对于彩色影像,应该分别计算各通道的灰度均值,并联立全部颜色通道来计算互相关系数,对应的计算公式为

ENCC=

(8)

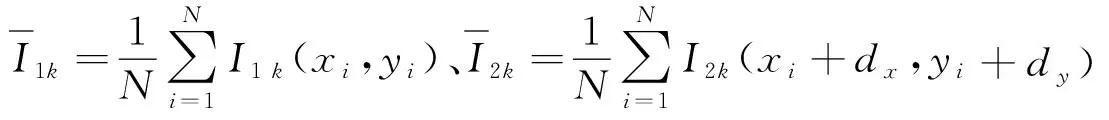
将匹配间隔设为m×n,即每隔m行、n列匹配一个同名点,间隔越小,密度越大,重建的精细程度越高,此值可根据实际场景的复杂程度来设置。对于左核线影像上任一待匹配点p1(x,y),根据该点处的视差估算其在右影像中的粗略匹配点为p2(x+dx,y+dy),并以该点为中心,在右影像第y+dy扫描行的[x+dx-r,x+dx+r]像素范围内进行一维搜索匹配。需要说明的是,虽然1.4.1节提到y视差并不固定,但在搜索区域的小范围内,y视差波动很小,故搜索时假设dy固定不变。由于粗匹配点p2的估算精度较高,因此搜索半径r不必很大,这一方面减小了搜索范围,提高了匹配效率,另一方面降低了误匹配的概率,提高了匹配正确率。

对于每个候选匹配点,根据式(8)计算以该点为中心的目标影像块(大小一般取11×11)与以p1为中心的源影像块间的归一化相关系数;从所有候选点中取相关系数最大的点,若该点的相关系数不小于t(t一般取0.7,避免遮挡导致的无对应点的情况,保证匹配的正确性),且该相关系数与次大相关系数之差大于某一间隔e(e一般取0.01,保证同名点具有一定的显著性,提高置信度),则认为是最佳匹配点;否则剔除该点。

在搜索最佳点时,采用如下2个策略来提高匹配效率。

(1)一维搜索时,将搜索步长设为2,即不是遍历[x+dx-r,x+dx+r]范围内的每一个像素,而是每间隔一个求一次相关系数,从而使搜索量减半,进而达到提高匹配效率的目的。这样做的合理性在于:由于搜索到的最佳匹配点都会采用最小二乘匹配进行微调,而最小二乘匹配的校正范围可以达到2个像素[21],所以即使实际最佳匹配点为未被扫描的间隔像素,而搜索到的最佳位置为其邻近像素,亦可通过最小二乘匹配来校正到实际的最佳位置,故无需逐点匹配。

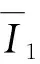
此外,沿扫描线对匹配点加入了顺序一致性约束,即对于左图某一核线上的两点p1、p2,对应的匹配点分别为p′1、p′2,由于p2位于p1的右边,则p′2必位于p′1的右边(从左向右扫描)。这样的处理进一步增强了匹配的可靠性。

1.5 最小二乘匹配

由于逐点搜索匹配仅能达到1个像素的匹配精度,所以最后采用最小二乘影像匹配[21]对搜索到的初始匹配点进行微调,使同名点达到亚像素级的匹配精度,以改善重建场景的视觉效果。由于最小二乘匹配能校正同名影像窗口的仿射变形,所以最终的相关系数应大于某一较大门槛(一般取0.9),才认为是正确的匹配点。

2 实验与分析

实验所用机器的软硬件配置如下:操作系统为64位windows10,处理器为AMD Ryzen 7 4800H,主频2.9 GHz,内存8 G。

利用小型无人驾驶飞机对某一村庄进行俯视航拍,航高约为300 m,所用相机为佳能5DⅡ,图像大小为5 616像素×3 744像素,全航区共拍摄了78(13幅×6航线)幅影像。

从上述数据中取一个立体像对,从左影像中均匀选取20个样本点,确保样本点覆盖各类典型地物、且纹理较为丰富;人工拾取各样本点在右影像的对应匹配点,拾取过程将影像放大8倍刺点,确保人工同名点达到较高精度。

对上述左影像样本点分别采用累积绝对差方法(sum of absolute differences, SAD)[22-23],和本文方法自动匹配右影像同名点,比较自动同名点与人工同名点(真值)的位置误差,结果如下。从表1可以看出,本文方法的各同名点位置误差均小于SAD方法,平均位置误差亦显著小于SAD方法,表明本文方法的匹配精度要明显优于SAD方法。

表1 使用SAD方法和本文方法的同名点位置误差比较Table 1 Comparison of the position errors of corresponding points using SAD method and proposed method

分别采用SAD方法和本文方法对该像对执行稠密匹配,匹配间隔设为5×5。图3是本文方法的匹配结果示意。表2是匹配耗时、最终点数、匹配点平均相关系数3项指标的统计结果,从表2中可以看出,本文方法的同名点数量较SAD方法要少,其原因是为了保证匹配的正确性,本文方法对部分不可靠的匹配点进行了剔除;本文方法的匹配耗时少于SAD方法,可见匹配效率得到了一定提高;本文

表2 使用SAD方法和本文方法的匹配统计结果比较Table 2 Comparison of matching statistical results using SAD method and proposed method

图3 稠密匹配结果Fig.3 Dense matching results

方法的全部同名点归一化相关系数均方值较传统方法显著提高,表明匹配准确性和精度明显优于SAD方法。

取其中10个像对,分别用SAD和本文方法进行稠密匹配,图4和图5分别是各像对的匹配耗时、平均相关系数两个指标的直方图统计结果。从图4和图5可以看出,每个像对采用本文方法的匹配耗时和平均相关系数均优于SAD方法,进一步证明了本文方法在匹配效率和精度方面的优势,同时也证明了本文方法的稳定性。

图4 10个像对匹配耗时比较Fig.4 Comparison of matching time of 10 image pairs

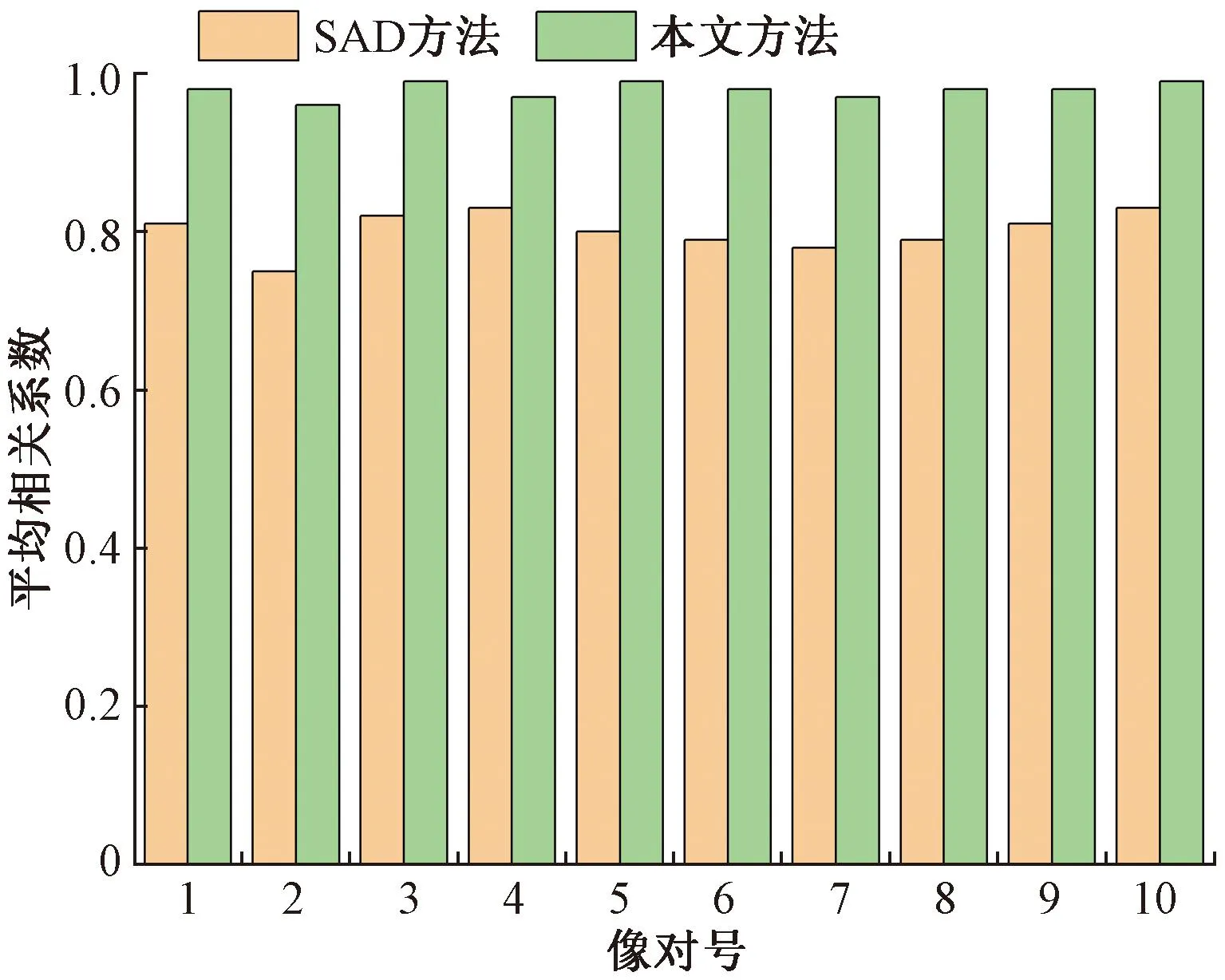
图5 10个像对平均相关系数比较Fig.5 Comparison of average correlation coefficients of 10 image pairs

由航区的全部影像通过特征匹配、相对定向共建立了64个立体像对模型,对这些立体像对进行稠密匹配,匹配间隔为4×4,每个像对提取的同名点数量为20多万至70多万个(根据场景的不同,匹配点数量有差异,因为对于纹理单一区域,很多点因可靠性低而被剔除),耗时约3.48 h。

通过三角测量[13]解算稠密点的空间坐标,得到稠密空间点云,图6是某个像对模型对应的空间点云,对每个空间点进行了纹理映射;图7是由稠密点云构网生成的三角网场景;图8是在三角网地形上贴纹理后生成的真实感场景;图9是拼接好的全景地形的正射视图,与传统的基于二维变换的航片拼接方法不同,此处的正射影像是根据精细三维模型通过正射校正生成,因此是真正射影像;图10是用伪彩色表示的全景稠密深度图(从红色到蓝色深度逐渐增加),从图10可清晰地看到,与图9影像相对应的地物(房屋等)轮廓,表明稠密深度图达到了较高的精细程度。

图6 空间点云Fig.6 Spatial point cloud

图7 网格场景Fig.7 Mesh scene

图8 纹理贴图三维场景Fig.8 Texture map 3D scene

图9 全景正射图Fig.9 Panoramic DOM

图10 全景伪彩色深度图Fig.10 Panoramic pseudocolor depth map

3 结论

提出了一种用于三维场景重建的航空遥感影像同名点稠密匹配方法。该方法以特征匹配同名点为基础,首先生成核线影像,并估算核线影像对的初始视差;然后在核线影像上进行基于核线约束的一维灰度相关搜索匹配;最后对灰度相关匹配结果做最小二乘匹配,从而使同名点达到亚像素级匹配精度。实验结果表明,本文方法可逐像素提取同名点,匹配的效率、精度和正确率均优于传统方法,且具有很好的匹配稳定性。