复合地层小直径隧道掘进机掘进速度区间预测

杨耀红, 韩兴忠, 张智晓, 刘德福, 孙小虎, 4

(1.华北水利水电大学水利学院, 郑州 450046; 2.河南省水圈与流域水安全重点实验室, 郑州 450046;3.中州水务控股有限公司, 郑州 450000; 4.中水北方勘测设计研究有限责任公司, 天津 300000)

隧道掘进机(tunnel boring machine,TBM)由于其方便、快速、经济和环保等优势,已逐渐在城市交通、煤矿巷道、水工隧洞建设等领域内广泛应用,尤其在国家水网的支线建设中,对于地形高差较大的地区,采用小直径TBM施工是必然选择。TBM对于施工地质条件极其敏感,特别在复合地层内掘进时,由于复合地层是在开挖断面范围内或开挖延伸方向上,由两种或两种以上岩土力学、工程地质和水文地质等特性上相差较悬殊的不同地层组成的[1],若TBM掘进参数与地质条件不匹配,TBM掘进效率下降,造成施工成本增加和工期延误等问题;同时,在开挖小直径隧洞时,TBM姿态控制及掘进参数设置更加困难,施工不确定性更强,TBM掘进速度(penetration rate,PR)变化更大。因此,准确预测复合地层小直径TBM施工掘进速度,是进行施工风险控制和估算施工工期等迫切需要解决的问题。

目前,中外学者提出了许多关于TBM掘进速度的预测模型,这些模型主要为理论模型、经验模型和人工智能模型[2]。理论模型主要是通过室内切割试验、数值模拟或基于施工现场资料的理论分析来展开对TBM掘进效率的预测研究。如Sanio[3]认为TBM滚刀破坏形式主要为岩体张拉破坏,并非剪切破坏,并开发了不同岩石内的滚刀破岩性能预测公式;Boyd[4]为解决传统回归分析和模糊神经网络建模时量纲不统一的问题,借助量纲分析方法来研究了当刀盘功率和隧道截面积确定时刀盘比能和机器效率因子与TBM掘进速度之间的关系,并得出了掘进速度预测公式;Ozdemir[5]基于实验数据开发了科罗拉多矿业学院滚刀破岩力模型(colorado school of mines,CSM)的第一个版本;Rostami等[6-7]对传统CSM模型进行了两次改进,该模型通过全尺寸线性切割机总结了大量影响TBM滚刀荷载的因素,并结合现场大量的TBM掘进数据和岩体参数得到了TBM掘进速度的预测公式。理论模型用于预测TBM掘进性能时,室内试验未完全反映自然形态下岩石特性以及环境因素的影响,并且理论模型通常将施工条件进行简化,从而使得模型简单,而TBM施工过程同步进行隧道开挖、渣土运输和支护系统的连续工作,因此,TBM掘进效率预测研究要基于施工现场实际情况开展。

经验模型是搜集以往施工现场数据形成大数据库,通过对数据库中岩机相互作用产生的数据进行挖掘来研究TBM掘进效率与各因素之间的关系。如Farmer等[8]利用8条不同TBM工程的地质数据和掘进数据,提出利用岩石抗拉强度和刀盘单刀推力来计算TBM刀盘贯入度;挪威科技大学根据大量施工TBM施工数据和地质数据,利用简单回归分析方式对岩体参数和掘进参数进行分析得到挪威科技大学(Norwegian University of Science and Technology,NTNU)模型,随着隧道类型的不断增加,NTNU模型先后经历了6次改进,最新版本是由Bruland[9]所提出;除NTNU模型之外,部分研究人员沿着质量分级原理,着手开发出了一些新的岩体可掘性系统,如Barton[10]利用搜集到的145条TBM掘进数据和地质数据,提出了TBM掘进速度、利用率和施工速度的TBM掌子面岩体质量指标(quality,QTBM);王健等[11]应用岩体分级系统,通过回归分析建立了与TBM性能掘进参数掘进速率、施工进度、利用率以及贯入度指数的经验公式。经验公式过度依赖历史数据,并且考虑因素较少,导致经验模型的普适性较差,所以在复杂施工环境条件下应用存在一定的局限性[12]。

近年来随着人工智能技术的快速发展,机器学习方法和深度学习技术在TBM掘进性能预测中得到了广泛应用。Samaei等[13]使用4个简单的回归分析方法研究了掘进速度与岩体参数之间的相关性,基于此,引入两个非线性多变量方程,并使用帝国主义竞争算法(imperialist competitive algorithm,ICA)、分类和回归树(classification and regression tree,CART)和遗传表达式编程(gene expression programming,GEP)来对方程进行优化[13];张弛等[14]以新疆某供水工程Ⅱ标段施工数据为依托,提取5种TBM上升段掘进参数和围岩等级信息并将其作为模型输入,以掘进稳定段总推力 和刀盘扭矩 为输出,建立了一种基于门控循环单元(gated recurrent unit,GRU)的TBM掘进参数预测模型;仉文岗等[15]基于纽约皇后输水隧道搜集到的数据,建立了基于随机森林(random forest,RF)的TBM掘进性能预测模型,并分别采用粒子群(particle swarm optimization,PSO)优化算法、遗传算法(genetic algorithm,GA)、差分算法(differential evolution algorithm,DE)和贝叶斯优化(Bayesian optimization,BO)来进行超参数优化调整。虽然这些基于人工智能技术构建的TBM掘进效率预测模型有着更好的普适性、操作性和精确性等优点,但对不同工程,不同预测模型预测精度也存在差别。

综上所述,经验模型、理论模型和人工智能技术大多是TBM掘进速度点/瞬时值预测模型。然而,TBM在施工过程中,受地质、机械、地下水、操作人员、施工组织管理等多种因素的影响,使TBM掘进速度呈现较大的不确定性。尤其在复合地层小直径条件下,施工空间狭小,地层组合复杂,TBM姿态较难控制,需要不断调整,所以,TBM掘进速度的不确定性更强。目前,大多数TBM掘进速度预测模型对这些不确定性和风险性都考虑不足,导致TBM掘进速度瞬时预测值的可靠性不足。如何考虑TBM施工中的不确定性,以提高掘进速度瞬时预测值的可靠性,是亟待解决的问题

本文研究考虑将预测结果的不确定性以区间的形式表示[16],引入区间预测模型来预测复合地层下TBM掘进速度。目前预测区间估计方法主要有德尔塔(Delta)法、贝叶斯(Bayesian)法、均值方差估计(mean-variance estimation,MVE)法、区间上下限估计(lower upper bound estimation,LUBE)法和拔靴(Bootstrap)法,其中,基于Bootstrap法的区间预测可以解决常规点预测模型中的不确定性误差,其通过重复抽样完成逼近样本分布特征并构造区间,具有计算简单,不需进行复杂的导数及定积分求解[17]以及精度高适用于小样本等特点。因而被广泛应用于滑坡位移预测[18-19]、电网风力发电预测等研究[20-22],Bootstrap方法在滑坡和发电预测方面的研究成果,对于受众多不确定性因素影响的TBM掘进速度预测研究,具有一定的借鉴意义。当前对于复合地层小直径TBM掘进速度的预测并未引入区间预测方法。若对PR进行区间预测估计,既能在一定程度上反映了PR的不确定性,又可以给出PR可靠的量化区间,以便为合理评估TBM施工工期和进行掘进参数优化提供参考。

现采用4种不同的Bootstrap抽样方法利用现场搜集得到的影响参数值和掘进速度值形成数据库,进行Q次有放回的等概率抽样,来构建Q个伪数据集,然后利用Q个伪数据集训练Q个核极限学习机(kernel extreme learning machine,KELM)模型对系统误差进行估计,同时训练单个反向传播神经网络(back propagation neural network,BPNN)模型来对随机误差进行估计,最终结合随机误差和系统误差,构造出采用4种Bootstrap方法,在置信水平为90%、95%、99%下的TBM掘进速度预测区间,并以南水北调安阳市西部输水隧洞工程为实例,来验证所建模型的有效性。

1 TBM掘进速度区间预测模型

1.1 区间预测Bootstrap方法

Bootstrap方法又称自助法或拔靴法,它是由统计学家Efron[22]在1979年提出的一种借助计算机技术来实现的统计抽样方法,该方法无需事先知道或者假定样本的分布情况,只通过对原始数据进行多次有放回的随机抽样,构成多个伪数据集来对总体分布进行估计推断。常用的4种Bootstrap方法的具体原理[23]如下。

(1)Pairs Bootstrap。Pairs Bootstrap方法,即从原始数据集中对目标值和输入值进行有放回的随机成对抽样,来得到伪数据集,通过伪数据集来进行假设检验和置信区间的估计。

(2)Moving Block Bootstrap。Moving Block Bootstrap方法,通过对原始数据进行随机分成L块处理,并对形成的新块数据进行有放回的随机抽样,从而构成用于假设检验和构建置信区间的伪数据集。

(3)Residual Bootstrap。Residual Bootstrap方法,将原始数据通过模型进行预测之后,计算出预测值与实际值之间的残差,将残差进行中心化处理,并对处理过的残差进行有放回的随机抽样,从而生成用于假设检验和构建置信区间的伪数据集。

(4)Wild Bootstrap。Wild Bootstrap方法,在Residual Bootstrap方法的基础上,将中心化残差与随机权重方法结合,生成带有随机权重的残差数据集,通过对残差数据集进行有放回的抽样,来得到一组用于假设检验和构建置信区间的伪数据集。一般随机权重的生成方式主要有以下两种。

第一种为Rademacher分布,即

(1)

第二种为Mammen分布,即

(2)

式中:β1、β2为随机权值;p为随机权值出现的概率。

1.2 核极限学习机(KELM)

KELM是一种简单前馈模型[24],包含输入层、隐含层和输出层,KELM主要是在极限学习机(extreme learning machine,ELM)的基础上引入核函数来提高模型的预测精度和计算速度,其主要原理为

F(x)=h(x)β=Hβ=L

(3)

式(3)中:x为神经网络输入特征;β为输出权重 向量;L为期望输出值;h(x)和H为特征映射函数或激励函数,其功能就是将模型输入层的数据由原本空间映射到ELM的特征空间。通过广义逆矩阵理论,输出权重β为

β=H*L

(4)

式(4)中:H*为H的广义逆矩阵。通过对式(4)引入对角矩阵I和正则化参数C,输出权重的最小二乘解可以表示为

(5)

通过引入核函数来将随机映射替换为稳定映射,来加强模型的稳定性并提升模型的泛化能力。通过引入核函数后,模型表达式为

ΩELM=HHT=h(xi)h(xj)=k(xi,xj)

(6)

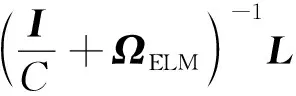
(7)

式中:I/C为核矩阵内对角线上元素的偏置常量,其功能是通过调整结构风险和经验风险之间的比例,来加强模型的稳定性并提升模型的泛化能力;ΩELM为核矩阵;k(xi,xj)为核函数。

由于RBF核函数相较于多项式核函数和线性核函数在处理高维向量内积问题中有着很好的优势[25],因此选取RBF核函数来作为KELM模型的核函数进行建模,RBF核函数其表达式为

k(xi,xj)=exp(-δ‖xi-xj‖2)

(8)

式(8)中:δ为核参数;‖xi-xj‖2为输入向量xi和输入向量xj之间欧氏距离的平方。

由于引入正则化参数和核参数,KELM模型中,对于以上参数的准确设置有着很高的要求,适宜的参数将会大幅度提高模型的预测性能,而且本文中KELM模型是核心模型,故正则化参数和核参数的设置也成为影响TBM掘进速度区间预测效果的关键参数,为了获得更为准确的预测结果,本文引入麻雀优化算法(sparrow search algorithm,SSA)[26]对正则化参数C和核参数δ进行优化。

1.3 优化的BP神经网络

BPNN是目前最常用的一种人工神经网络,其结构主要包括输入层、隐含层和输出层,其计算原理是通过从后向前反向传播误差来不断调整权重值和阈值的大小,来达到减小误差的目的[27]。由于BPNN模型结构单一并且自我学习能力较强,因此被广泛应用于解决内部机制复杂的问题。但是BPNN初始网络权值和神经元阈值是随机产生,并且迭代次数多、网络收敛速度较慢,导致无法保证每次迭代都达到全局极值。为了解决以上不足,部分学者通过引入智能优化算法来得到最优权值和阈值,如粒子群算法和遗传算法,但是这两种算法在收敛速度方面不是太理想[28-29]。因此本文研究中通过麻雀优化算法(SSA)来对BPNN神经网络进行改进,运用麻雀优化算法(SSA)自身局部搜索能力强和收敛速度快等特点来对BPNN权值和阈值进行寻优计算,从而得到更为准确的BPNN参数,来提高模型预测能力。

1.4 TBM掘进速度区间预测流程

本文所建Bootstrap-KELM-BPNN模型的基本预测流程如图1所示,主要包括4个步骤:①通过抽样方法构建伪数据集;②KELM模型训练多个模型,并计算得到系统误差方差的估计;③BPNN模型训练集随机误差方差的估计;④TBM掘进速度预测区间构造。

图1 区间预测流程图Fig.1 Interval prediction flowchat

1)构建伪数据集

将原始数据集D通过式(9)进行归一化后,将数据划分为训练集Dtrain和Dtest,然后分别采用Pairs Bootstrap、Moving Block Bootstrap、Residual Bootstrap和Wild Bootstrap 4种抽样方法对训练集Dtrain进行有放回的随机重抽样,并且每次重抽样的抽样数与训练集样本数应保持一致,经过Q次抽样之后构建Q个Bootstrap伪数据集。

(9)

式(9)中:x为神经网络输入特征;xmax、xmin为输入特征的最大值和最小值;x′为标准化后的输入特征。

2)多个KELM模型训练及系统误差的方差估计

将SSA和KELM相结合,对基于Dtrain训练集建立的多个KELM模型核参数δ和正则化参数C进行寻优,其中SSA算法的基本参数设计如下:①麻雀数量为50;②设定最大迭代次数为60;③δ和C寻优区间分别为[0.1, 10]和[0.1, 50][30];④发现者和侦察者个数分别为0.4和0.6。适应度函数为均方误差MSE,即

(10)

(11)

(12)

3)ANN模型训练及随机误差的方差估计

为准确构建TBM掘进速度预测区间,除了确定模型的系统误差的方差,还需确定模型随机误差的方差。随机误差的方差可由式(13)计算得

(13)

(14)

(15)

利用平方残差数据集训练BPNN模型时,使得观测样本在Dr2中出现的概率最大,所以引入极大似然估计,建立了新的目标函数CB,其表达式为

(16)

4)TBM掘进速度预测区间构建

(17)

(18)

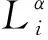
1.5 区间预测模型性能评价指标

区间预测基于某一置信水平下对目标值取值范围的估计,一般通过区间的可靠程度和清晰程度来评估区间预测模型的性能。其中,可靠程度一般通过预测区间覆盖率(prediction interval coverage probability,PICP)来评估,而清晰度则是以平均预测区间宽度(mean prediction interval width,MPIW)来评估。PICP和MPIW的具体表达式为

(19)

(20)

(21)

式中:Ntest为测试样本数;ci为布尔型变量,若区间覆盖点预测值,ci取1,反之,ci取0。

一般来说,区间覆盖率PICP越高,区间平均宽度MPIW越小,说明预测区间质量更高[31]。然而在实际预测过程中,PICP和MPIW往往是矛盾的,要使PICP很高,就需要增大MPIW,人们希望在保证PICP很高的前提下,保证MPIW很小。为了解决该问题,引入了宽度范围综合指标(coverage width-based criterion,CWC)作为PICP和MPIW的补充评价指标[32],来评估预测区间的质量。其具体计算表达式为

CWC=MPIW[1+γPICPe-η(PICP-μ)]

(22)

(23)

式中:γ为布尔型变量,若PICP≥μ时,γ取0,此时CWC=PICP,反之,γ取1;η为惩罚参数,取值一般偏大,来区分PICP和μ的区别;μ为置信水平,即μ=(1-α)×100%。

2 模型应用

2.1 工程地质情况

南水北调安阳市西部调水工程位于安阳市西部,工程穿越山丘区段,自下堡村西北(中联水泥路矿场道路西侧坡地,桩号17+738)至横水镇范家庄(30+918)段,全长13.18 km。隧洞工程主要包括TBM掘进段、钻爆段、TBM始发场地、TBM接收场地及钻爆洞口场地等,具体布置如图2所示。其中:桩号18+896～30+718为TBM掘进段,长11 822 m,比降0.01%,采用圆形断面,开挖直径4.33 m,设计断面尺寸直径3.5 m。采用一台双护盾TBM掘进施工,TBM设计参数如表1所示,纵向设计坡度为0.01%,平面设计有一处转弯,转弯半径为1 500 m。

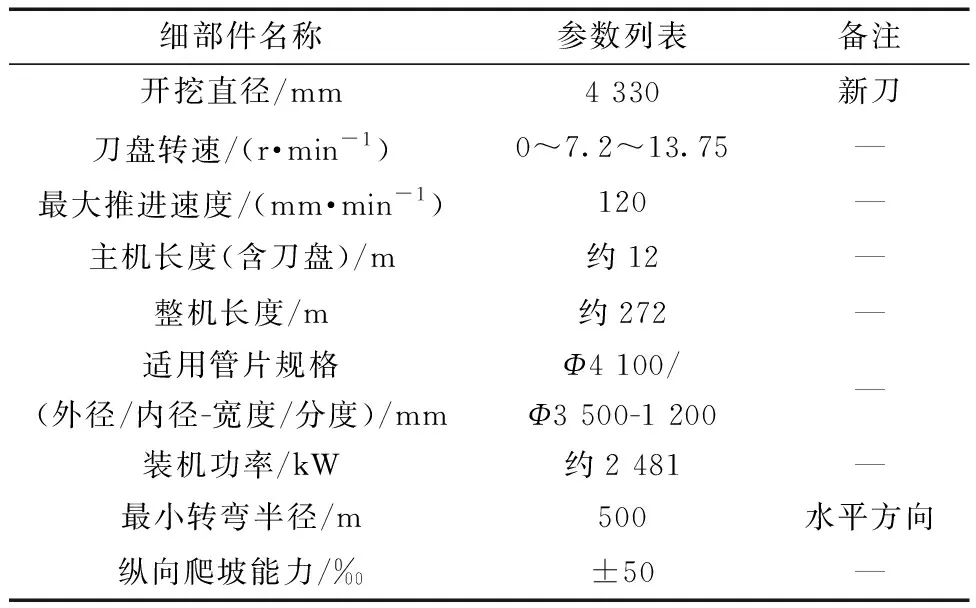
表1 TBM设备主要设计参数表Table 1 Table of main design parameters of TBM

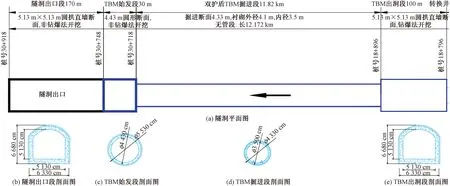
图2 隧洞总体布置图Fig.2 General layout of the tunnel

根据工程地质勘测报告,工程隧洞段表层为第四系地层覆盖,洞身穿越大都为石灰岩,围岩类别主要为Ⅲ类(13.98%)、Ⅳ类(24.46%)和Ⅴ类(61.11%),并且岩石节理裂隙发育,裂隙中钙质及泥质充填。施工过程中发现部分地段施工掌子面为土石复合体,根据现场地质描述报告,掌子面上中部为黄色泥土,其余为深灰色、灰褐色局部夹薄层白云质灰岩,如图3所示。

图3 TBM施工掌子面地质概况Fig.3 Geological overview of the palm surface of TBM construction

2.2 模型输入参数选择

影响TBM掘进速度的主要掘进参数为推力、贯入度、扭矩、刀盘转速和刀盘功率,岩体参数中主要为单轴抗压强度强度和岩体完整性系数。TBM掘进是一个岩机相互作用的复杂过程,选择场切深指数(field penetration index,FPI)和转矩贯入度指标(torque penetration index,TPI)来表征岩体力学信息。因此本文模型最终选取FPI和TPI、刀盘总推力、刀盘功率、刀盘扭矩、刀盘贯入度和刀盘转速为主要输入参数,其中,FPI和TPI具体计算表达式为

(24)

(25)

式中:Fn为刀盘总推力;n为刀具数量;Td为刀盘扭矩;p为贯入度。

本文研究数据包含142组FPI、TPI、掘进参数(刀盘总推力、刀盘功率、刀盘扭矩、刀盘贯入度、刀盘转速和掘进速度PR),其中PR与FPI、TPI和其他掘进参数的皮尔逊相关系数如表2所示。

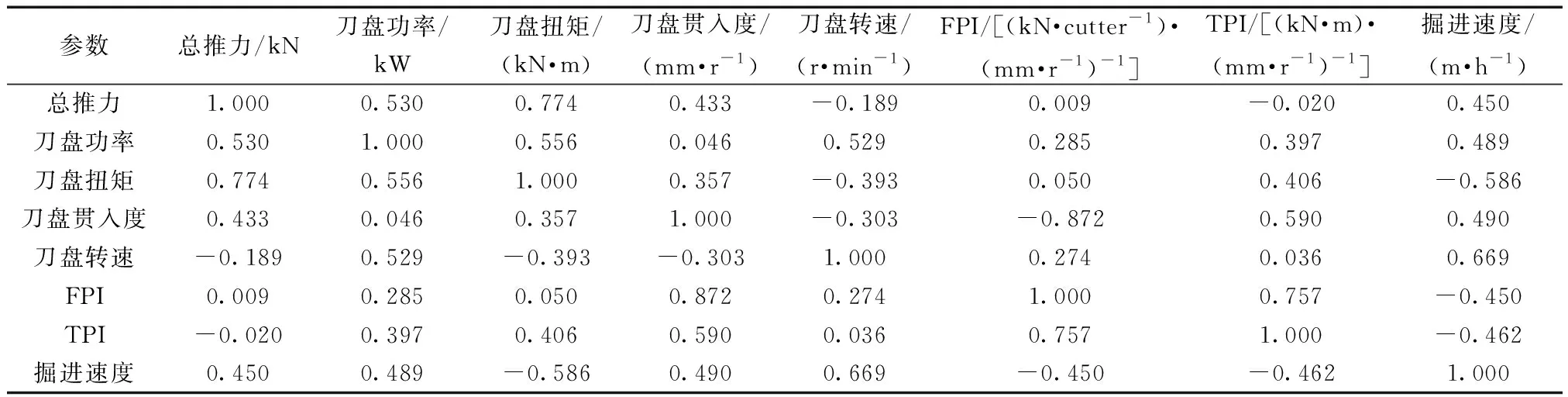
表2 参数相关性分析表Table 2 Parameter correlation analysis table

通常皮尔逊相关性系数R在0.6～0.8时,代表相似程度强;R在0.4～0.6时,代表相似程度较强;R在0～0.4时,代表相似程度弱[33]。如表2所示,掘进速度与各大参数都存在较强的相关性,因此选择以上7个参数作为模型的输入是可行的。

2.3 Bootstrap关键参数选择

Bootstrap主要是通过对观测样本进行重抽样,来实现对总体分布特性判断的统计方法。在重抽样过程中,抽取样本次数以及每次形成的样本容量的准确设置是保证模型精准预测的前提条件。样本容量一般与测试集原数据样本容量保持一致,本文测试集容量为20,所以每次形成样本容量为20;重抽样次数Q取值范围一般在20～200。过大的抽样次数并不能显著提高预测区间的质量[32,34],因此,本文中Q取20次。

2.4 模型区间预测结果及验证

Bootstrap-KELM-ANN预测模型主要是构建在100%×(1-α)置信水平下,来计算TBM掘进速度的预测区间,构造预测区间是为了将施工过程中和建模过程中的不可控因素考虑进去,为施工风险控制及决策提供了依据。一般在实际应用过程中,为了取得更为精确的区间,选取的置信水平为90%、95%和99%,并在不同置信水平下的TBM掘进速度预测结果进行比较分析。

将采集到的142组原始数据划分为122组训练集和20组测试集,采用2.2节中叙述的不同Bootstrap方法对训练数据进行抽样,并对模型进行训练,然后用测试集来验证本文模型的精确性,测试集预测结果如表3所示。随着置信水平的提高,预测区间宽度MPIW也在逐渐增大,并且在90%的置信水平下,Moving Block Bootstrap方法和Residual Bootstrap方法所得的CWC明显高于MPIW,所以该两种方法无法为TBM掘进速度预测施工风险控制和决策提供可靠的区间预测结果。对于Pairs Bootstrap和Wild Bootstrap方法而言,在不同置信水平下所得到结果都相对适中,其中Pairs Bootstrap和基于Mammen分布的Wild Bootstrap方法随着置信水平的提升,预测区间并未将预测结果完全覆盖,而基于Rademacher分布的Wild Bootstrap方法所获得的预测区间的CWC相对较小,而且在保持较高的PICP下获得较低的MPIW,并且自始至终将PR实测值曲线完全包络在内,所以可靠度相对较高。因此,通过对比预测精度发现,选择基于Rademacher分布的Wild Bootstrap方法作为预测模型的重抽样方法是合适的。

表3 测试集区间预测结果Table 3 Test set interval prediction results

可靠的区间预测结果中,其区间覆盖率PICP尽量接近于置信水平μ,即平均覆盖误差(average coverage error,ACE)[17],其计算方法为

ACE=PICP-μ

(26)

ACE值尽可能接近于0,通过计算在90%、95%和99%3种置信水平下TBM掘进速度的平均覆盖误差ACE分别为10%、5%和1%,因此,在99%置信水平下得到的区间能将掘进速度实测值完全覆盖,并且可靠程度高于95%和90%置信水平下所得到的预测区间,因此将在99%水平下得到的预测结果作为最终结果。

在置信水平为99%时,基于Rademacher分布的Wild Bootstrap抽样方法为主的Bootstrap-KELM-BPNN模型区间预测结果如图4所示。显然,该模型得到了很好的预测结果,并且得到了清晰可靠的预测区间,并将TBM掘进速度实测值完全覆盖在区间内,还通过区间宽度的变化,较好地解释了TBM施工过程中风险因素对TBM掘进速度的影响。

从图4可以看出在1、13、16时段,区间宽度明显宽与其他时段,区间宽度越宽说明可以容纳更大的不确定性。通过查阅地质报告可知,序号1、13和16正好对应于实际施工中2020年11月7日、2020年11月20日和2020年11月23日,在这3 d时间中,TBM施工掌子面如图5～图7所示。

图5 2020年11月7日施工掌子面Fig.5 Palm surface construction on November 7, 2020

图6 2020年11月20日施工掌子面Fig.6 Palm surface construction on November 20, 2020

图7 2020年11月23日施工掌子面Fig.7 Palm surface construction on November 23, 2020

2020年11月7日施工掌子面下部为黄色泥土,其余部位为深灰色、灰褐色局部夹薄层白云质灰岩;20日上左中部为灰色、灰褐色石灰岩,下部为角砾状灰岩,右部为黄色黏性泥土;23日掌子面整体都为黄色黏性泥土。通过分析得知TBM在7日、20日和23日内掘进地层为复合地层,将3种不同复合地层段的4个关键掘进参数(总推力、刀盘贯入度、刀盘扭矩和刀盘转速)分别记录,并将记录数据分别标记为复合地层段1、复合地层段2和复合地层段3,将记录数据与常规围岩掘进数据(Ⅲ类围岩段)进行对比分析,对比结果如图8所示。

图8 复合地层段与Ⅲ类围岩段掘进参数对比图Fig.8 Comparison diagram of driving parameters between mixed faced ground section and class III surrounding rock section

从图8(a)可以看出,Ⅲ类围岩下,总推力保持在1 100～1 300 kN,而在复合地层段1、复合地层段2和复合地层段3内总推力最低为2 500 kN,最高可达4 500 kN,远高于Ⅲ类围岩下的总推力;刀盘转速如图8(b)所示呈现四段分布,从高到低依次为,Ⅲ类围岩段大约为4.0 r/min,复合地层段2内转速在2.9～3.5 r/min内波动,复合地层段3内转速在2.5～3.2 r/min内波动,复合地层段1内转速在2.3 r/min左右波动;图8(c)中刀盘扭矩在复合地层段2和复合地层段3内介于600～900 kN·m,而复合地层段1内和Ⅲ类围岩段刀盘扭矩处于100～420 kN·m,普遍低于复合地层段2和复合地层段3;图8(d)中刀盘贯入度在Ⅲ类围岩段达到最高为14～16 mm/r,而复合地层段1、复合地层段2和复合地层段3较低,波动范围依次为4～12.8 mm/r,3～7.6 mm/r和3.8～13 mm/r。

通过对比发现在Ⅲ类围岩段保持较低的推力和扭矩时,可以得到较高的刀盘转速和刀盘贯入度,而在其他3种复合地层段内,推力和扭矩都高于Ⅲ类围岩段,并且刀盘转速和刀盘贯入度普遍较低,尤其是在复合地层段2和复合地层段3内,在极高的推力和扭矩下,得到的贯入度为最低,而且贯入度曲线呈现很强的波动性。综上所述,Ⅲ类围岩段与复合地层中掘进参数存在很大的差异,并且在Ⅲ类围岩段中掘进参数波动较缓,而在复合地层中掘进参数具有很强的波动性,因此,在复合地层中预测TBM掘进性能难度要更大于Ⅲ类围岩段。

通过以上分析可知,该模型在得到较强可靠性区间的同时,能较好地解释TBM施工过程中的不确定性,并且预测区间宽度MPIW可作为TBM施工过程中衡量风险预警的指标,能有效预测掘进过程中存在较大风险性的时段,提前采取相应措施,来降低施工风险。

2.5 预测结果分析

本文所用的区间预测理论在TBM掘进性能预测领域内应用较少,并且安阳项目工程资料以及施工数据有限,因此建立的TBM掘进速度区间预测模型的有效性,需要用更多的实际工程数据去验证。同时文中采用的4种主要重抽样方法其适用范围也存在一定的差异[23]:①Residual Bootstrap适用于输入元素与误差项相互独立,并且误差项服从独立同分布的模型;②Pairs Bootstrap适用于输入项中包含输出项的滞后项和误差项存在形式未知的异方差模型;③Moving Block Bootstrap方法主要适用于数据与误差项存在一定相关性的模型;④Wild Bootstrap与Residual Bootstrap方法类似,适用于输入因素与误差项相互独立且误差项具有异方差的模型,与Residual Bootstrap方法有所不同的是,当误差项的条件分布渐近对称时,基于Rademacher分布的Wild Bootstrap方法比其他形式更有效;当误差项的条件分布渐近非对称时,基于Mammen分布的Wild Bootstrap方法比其他形式更有效。

对于实际TBM掘进速度来说,实际采集数据是随时间增长而连续变化的时间序列。TBM掘进速度时序变化特征与开挖隧洞地质情况及其他不确定性因素所决定,其变化特征可能有3种形态,依次为平稳且具有同方差性的(震荡型变化曲线)、高度非平稳和异方差性(阶跃型变化曲线)、平稳且较为光滑的(光滑型变化曲线)。从方法实用性角度而言,上述4种Bootstrap方法在TBM掘进速度区间预测中的适用范围大致如下:①Pairs Bootstrap法、Residual Bootstrap和Moving block Bootstrap法在具有光滑型PR变化曲线(正常掘进段TBM掘进速度数据变化)上应用效果较好;②Pairs Bootstrap 法和Residual Bootstrap法也可能适用于TBM掘进速度数据为震荡型(TBM掘进速度稳定段数据)曲线变化情况;③Wild Bootstrap法适用于具有TBM掘进速度数据为阶跃型(隧洞地质情况极差时)曲线变化情况。显然,4种方法在实际TBM掘进速度数据变化情况中适用范围存在一定的交叉,因此单独从方法的适用性分析,并不能直接判断出哪一种方法最适合。

此外,在诸多实际回归预测问题中,输入元素一般是固定保持不变,并且输入因素取值范围往往决定了自身携带信息量的多少,显然,在采用何种重抽样方法时,都会在抽样形成伪数据集时都会出现不同程度的信息丢失,所以,选择哪种抽样方法能将信息的丢失控制在可控范围之内是当前研究值得考虑的一个重要问题。

综上所述,在应用Bootstrap方法展开TBM掘进速度区间预测研究时,应该从方法的适用性和实用性进行分析,从而选取与PR实测数据变形特征相契合的Bootstrap方法来进行区间预测。如图9所示,TBM掘进速度实测值变化曲线呈现阶跃式变化,并结合表3预测结果对比分析,发现基于Rademacher分布的Wild Bootstrap方法能够得到最为可靠的预测区间,明显适合于TBM掘进速度数据具有阶跃型曲线变化特征的类似工程进行区间预测。

图9 TBM掘进速度实测值变化曲线Fig.9 TBM tunneling penetration rate measurement value change curve

3 结论

(1)目前对于TBM掘进速度预测研究都集中于点预测,此类模型可以得到相对较高的精度,但是并不能对结果的可信度进行有效的表示。针对此类问题,结合南水北调安阳输水工程,本文研究提出了基于不同抽样方法的Bootstrap-KELM-BPNN区间预测方法,为定量评价TBM施工过程预测模型和输入数据等条件中包含的不确定性对预测结果的影响提供了一种有效的手段。

(2)基于4种常见的Bootstrap重抽样方法建立了TBM掘进速度区间预测模型,比较区间预测模型结果发现,4种方法都取得了较好的结果,其中,基于Rademacher分布的Wild Bootstrap方法在90%、95%和99%置信水平下取得了更好的精度,使得获取的区间能将TBM掘进速度实测值完全包络在区间内,并且在置信水平为99%时,模型预测区间可靠性更强。

(3)构造的预测区间对不确定性容纳能力随着置信水平的提高而增加,并且区间宽度能够与TBM施工过程中的不确定性相互对应,验证了区间预测模型对施工过程中不确定性的解释能力。

(4)在实际应用过程中,模型预测所得到的区间宽度是随着不确定性因素的动态改变而不断发生变化,因此,预测区间宽度的变化情况,可以作为评价点预测结果准确性和可靠性的补充,对于TBM施工风险控制与决策有一定的参考意义。