活用几何意义凸显直观想象核心素养——以2022 年新高考Ⅰ卷导数解答题为例

广东省东莞市常平中学(523570)蔡心耿

1 题目及解答

题目已知函数f(x)=ex-ax和g(x)=ax-lnx有两个相同的最值.

(1)求a;

(2)证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,且从左到右的三个交点的横坐标成等差数列.

解法1(1)a=1(过程从略);

(2)对于f(x),x∈R,f′(x)=ex-1,当x∈(-∞,0)时,f′(x)＜0,f(x)单调递减;当x∈(0,+∞)时,f′(x)＞0,f(x)单调递增,f(x)min=f(0)=1;对于g(x),x∈(0,+∞),g′(x)=当x∈ (0,1) 时,g′(x) ＜ 0,g(x) 单调递减; 当x∈(1,+∞) 时,g′(x)＞0,g(x) 单调递增,g(x)min=g(1)=1;

先证f(x)=ex-x与g(x)=x-lnx有唯一交点,即证:ex+lnx-2x=0 在(0,+∞) 有唯一解,令h(x)=ex+lnx-2x,h′(x)=ex+-2 ≥0,故h(x)在(0,+∞)单调递增,当x=当x=1,h(x)=e-2＞0,故存在唯一x1∈(0,+∞),使得x1-lnx1,因为故(lnx1,b)在f(x)上,故在g(x) 上,且故有从左到右不同三点这三点横坐标满足证毕.

解法2(几何意义1)f(x)=ex-x=|ex-x|(ex＞x) 的几何意义可看作为曲线y=lnx上一点B(ex,x) 到y=x的水平距离的函数(即距离|BC|),g(x)=x-lnx=|x-lnx|(x＞lnx)的几何意义可看作为曲线y=ex上一点A(lnx,x)到y=x的水平距离的函数(即距离|AC|),如图1.

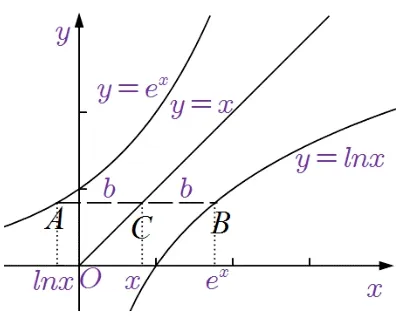
图1

故原题意等价于证明存在水平距离长度为b＞0 及x1,使得b等于上述两水平距离,即b=f(x1)=g(x1),且三个点横坐标成等差数列,即成等差数列.

取x＞0,y=ex上一点A(lnx,x) 到y=x的水平距离为g(x)=|x-lnx|=x-lnx(x＞lnx),y=lnx上一点B(ex,x) 到y=x的水平距离为f(x)=|ex-x|=ex-x(ex＞x),先证x-lnx=ex-x有唯一解.同解法1 证得:存在x=x1是方程ex+lnx=2x在(0,+∞)唯一解,即成等差数列,此时取即b=f(x1)=g(x1),证毕.

解法3(几何意义2)f(x)=exx的几何意义可看作为曲线y=ex上一点D(x,ex)到y=x的铅垂距离函数(即距离|DC|),g(x)=x-lnx的几何意义可看作为曲线y=lnx上一点E(x,lnx)到y=x的铅垂距离函数(即距离|CE|),如图2.

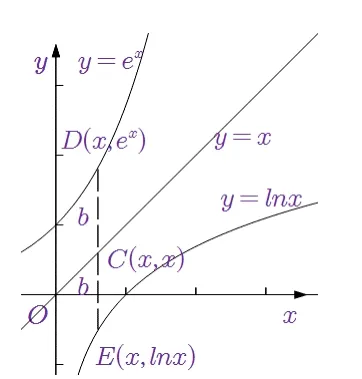
图2

故原题意等价于证明存在铅垂距离长度为b＞0 及x1,使得b等于上述两铅垂距离,即b=f(x1)=g(x1),且三个点纵坐标成等差数列,即成等差数列.

取x＞0,y=ex上一点D(x,ex)到y=x的铅垂距离为f(x)=ex-x,y=lnx上一点E(x,lnx)到y=x的铅垂距离为g(x)=x-lnx,先证x-lnx=ex-x有唯一解.同解法1 证得:存在x=x1是方程ex+lnx=2x在(0,+∞) 唯一解,即成等差数列,此时取即b=f(x1)=g(x1),证毕.

解法4(几何意义3) 对数函数y=lnx图像上任意不同的两点A(ex,x),B(x,lnx)(0 ＜lnx＜x＜ex),如图3,记两点的纵坐标增量为Δy=x-lnx=g(x),横坐标增量Δx=ex-x=f(x),原题意等价于证明存在实数b及x1,使得即割线AB斜率且lnx1,x1,ex1成等差数列.

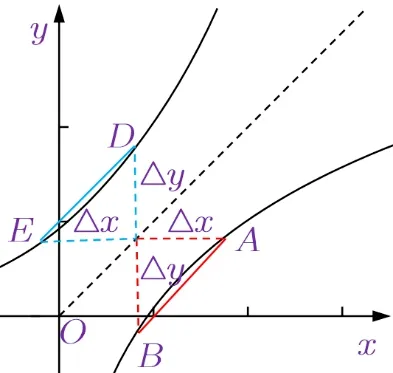
图3

评析解法2、解法3 和解法4 分别运用了f(x)与g(x)的不同的几何意义解题.

有意思的是将图1 和图2 两图合起来就成了正方形,这与文[1]的证法3 有异曲同工之妙,如图4.

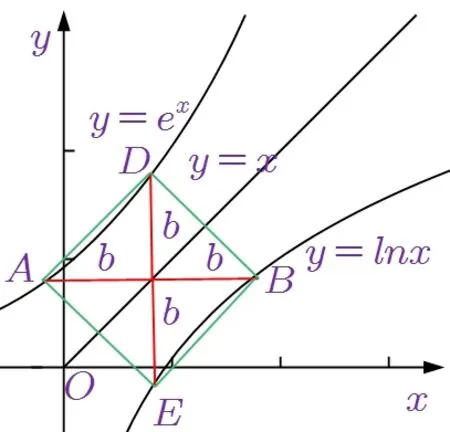
图4

解法4 是将f(x) 与g(x) 理解成y=lnx上A(ex,x),B(x,lnx)(x＜ex)两点连线的因变量增量和自变量增量,进而转化证明割线斜率值为1,这时“1”也为y=x的斜率,即割线平行y=x.当然,我们也可以将f(x)与g(x)理解成y=ex上两点D(x,ex)和E(lnx,x)连线的因变量增量和自变量增量,进而转化证明割线斜率值为1,如图3.图3 与图4 也有貌离神合之妙.

上述利用几何意义解法体现了数形结合的数学思想方法,凸显直观想象的数学核心素养.

2 试题探源

2.1 母题溯源

溯源题目1(2013 年高考江苏卷) 设函数f(x)=lnx-ax,g(x)=ex-ax,其中a为实数.

(1) 若f(x) 在(1,+∞) 上是单调减函数,且g(x) 在(1,+∞)上有最小值,求a的取值范围.

(2)若g(x)在(-1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.

评析这两道高考题中主体函数f(x)=lnx-ax、g(x)=ex-ax是一致的,只是题设不同:江苏卷的题目更多考察这两个含参函数各自性质,而2022 年新高考Ⅰ卷第22题更多考察f(x)与g(x)两函数图像之间的性质,如距离与对称性等,这提示我们在备考中,应当注重真题的研究,同时,注重学生数学核心素养的培养.

2.2 教材探源

第一,新教材必修第一册中,介绍了基本初等函数y=ax,y=x,y=logax(a＞0 且a̸= 1) 三者的关系:y=ax图像与y=logax图像关于y=x对称,并称y=ax与y=logax(a＞0 且a̸= 1)为互为反函数,而且介绍了新教材中y=ax,y=x,y=logax(a＞1)这三个图像增长速度快慢问题,特别是y=ex,y=x,y=lnx三者增长速度快慢问题,所以作为教师应结合函数图像,加强对基本概念对比教学,发展学生直观想象,提升数学核心素养.

第二,上述新教材必修一第一册从几何直观感性角度来介绍y=ex,y=x,y=lnx三者增长速度快慢,而在新教材选择性必修第二册的导数章节课后习题从理性代数证明方式给出了lnx,x,ex的大小关系:lnx＜x＜ex(x＞0).

结合上述两点可知,这三个基本初等函数在教材中出现的频率颇高,可见这是我们复习备考的重点.总之,2022 新高考Ⅰ卷导数压轴题很好地践行“价值引领、素养导向、能力为重、知识为基”命题原则,加大了改革力度,突出了对学生能力与数学学科核心素养的考查.

3 推广

3.1 横向推广

命题1已知函数证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,且从右到左的三个交点的横坐标成等比数列.

证明f(x)=的几何意义可看作为曲线y=lnx上一点A(ex,x) 到原点连线的斜率函数,记为几何意义为曲线y=ex上一点B(lnx,x)到原点连线的斜率的倒数函数,记为即故题意等价于证明存在斜率值为b及x0(x0̸=1),使得且三点横坐标成等比数列,即成等比数列,如图5.

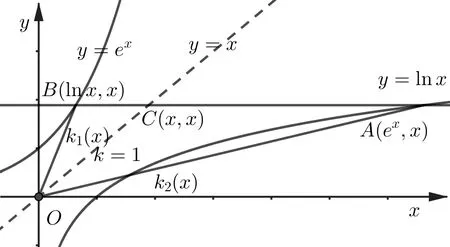
图5

先证k1(x)=有唯一解.即证有唯一解.变形得方程exlnx-x2=0 在(0,+∞)有唯一解,显然x=1 不是上述方程的解.

评析既然是推广,那么我们也应该从几何意义来解析,于是我们从f(x)与g(x) 的斜率和斜率倒数的几何意义出发,除了类比得到成等比数列之外,还有得到比较有趣的结论(参见图6).

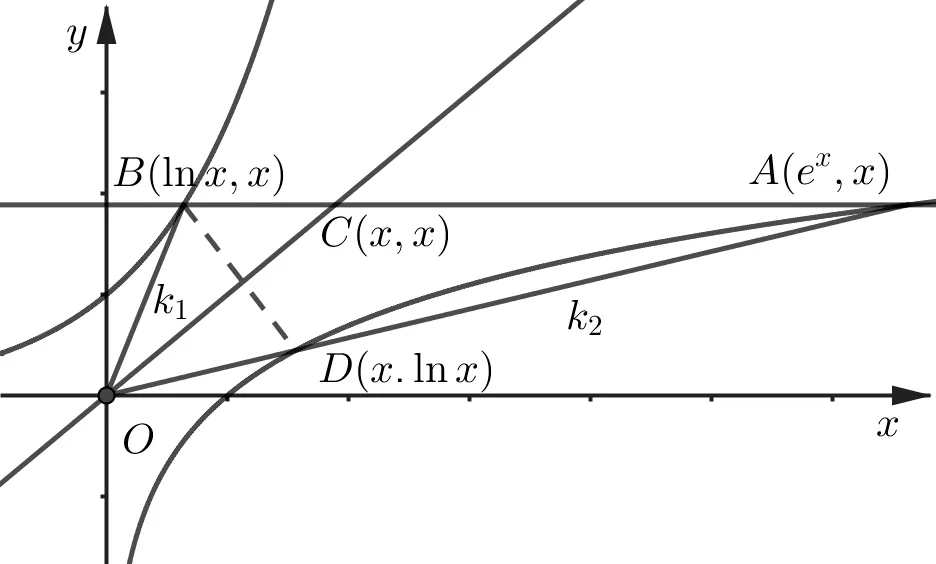
图6

其一,k1(x0)·k2(x0)=1,且这里的“1”就是y=x的斜率k=1,即直线OB与直线OA关于y=x对称;

其二,设直线OA交于y=lnx另一点D(x,lnx)(x＜ex),则点B与点D关于y=x对称; 反之,若点B与点D关于y=x对称,则O,D,A三点共线.

3.2 纵向推广

命题2已知函数f(x)=ax-x和g(x)=x-logax,证明:存在直线y=b,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,且从左到右的三个交点的横坐标成等差数列.

证明1°先证y1=ax与y2=logax,无交点.由于y=ax图像与图像关于y=x对称,两者为互为反函数,故只需证y=ax与y=x无交点即可,即ax-x=0 无解.

2°f(x)=ax-x的几何意义为曲线y=logax上一点B(ax,x) 到y=x的水平距离;g(x)=x-logax的几何意义为曲线y=ax上一点A(logax,x)到y=x的水平距离.故原题意等价于证明存在水平距离长度为b＞0 及x0使得b等于上述两水平距离,即b=f(x0)=g(x0),且成等差数列,图像请参考图1

取x＞0,y1=ax上一点A(logax,x) 到y=x的水平距离为x-logax,y2=logax上一点B(ax,x)到y=x的水平距离为ax-x,需证x-logax=ax-x有解.令先证h′(x)＞0 在(0,+∞)恒成立,即证令令m(x)=-2(lna)2x2+lna·x+1=0,解得x1=

当x∈(0,x2),F′(x)＞0,F(x) 单调递增,当x∈(x2,+∞),F′(x) ＜0,F(x)单调递减,故当时,(因为故h′(x)＞0 在(0,+∞)恒成立,h(x)=ax+logax-2x在(0,+∞)单调递增,当x→0+,h(x)→-∞,当x→+∞,h(x)→+∞,故存在唯一x0∈(0,+∞),使得h(x)=ax+logax-2x=0,即故成等差数列,此时取即b=f(x0)=g(x0),证毕.

注关于的证明:只需证exlna＞x,即证xlna＞lnx,构造函数n(x)=xlna-lnx即可,请读者自证.

4 结束语

直观想象是一种特殊的数学能力[2],它通过“形”的想象,研究变化趋势,预测变化结果,达到指引解决问题的方向、优化运算的目的,同时也是数形结合思想方法上的呈现形式.善于利用图形等几何语言对代数知识进行解析,引导学生从几何角度审视代数的问题,时常会有不一样的解决问题的途径.我国著名数学家华罗庚先生曾说过:“数缺形时少直观,形少数时难如微”,可见数形结合思想方法的重要性.