“平面直角坐标系”解题秘籍

2020-08-10方燕娟

中学生数理化·七年级数学人教版 2020年4期

方燕娟

“平面直角坐标系”这一章主要包括平面直角坐标系的有关概念、用坐标表示地理位置和用坐标表示平移等内容，但由于同学们初次接触“平面直角坐标系”，而且本章有较多需要熟记且容易混淆妁知识点，导致同学们在解题时总是不太得心应手.为了使同学们在成为学霸的路上少走弯路，特奉上一份“乎面直角坐标系”的解题秘籍，敬请阅读.

秘籍一：基础题得分要领——概念清晰

例1在平面直角坐标系中，描出点A（3，-2），B（0，3）的位置.

错解：如图1.

解析：错在忽视了坐标的顺序和坐标的符号，点的坐标顺序是“横坐标，纵坐标”.点A的坐标符号为（+，一），点A应该在第四象限，点B应该在y轴上，

要正确解答这类题，同学们一定要掌握象限内的点、x轴及y轴上的点的坐标的特征：

第一象限（+，+），第二象限（一，+），第三象限（一，一），第四象限（+，一）.

x轴上的点的纵坐标为0，表示为（x，0）.

y轴上的点的横坐标为O，表示为（0，y）.

正解：点A（3，-2）的位置如图2所示.而点B的横坐标为0，所以点B应该在y轴上，如图2所示，

例2若点P（3，a-1）到两坐标轴的距离相等，则a的值为____ .

错解：因为点P到两坐标轴的距离相等，所以a-1=3.解得a=4.

解析：没有掌握平面直角坐标系内一点P（x，y）到坐标轴的距离的含义.

（1）点P（x，y）到横轴的距离等于纵坐标的绝对值|y|.

（2）点P（x，y）到纵轴的距离等于横坐标的绝对值|x|.

正解：因为点P到两坐标轴的距离相等，所以|a-1|=|3|，解得a=4或a=-2.

例3已知点A（1，2），AB//x轴，若AB=2.则点日的坐标为

错解：填“（3，2）”，

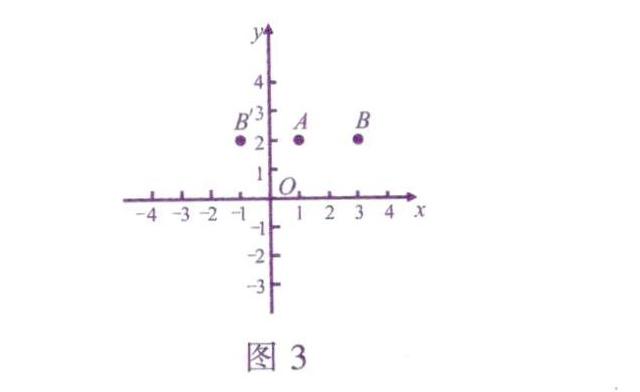
解析：点B可以在点A左右两侧，错解只填了点B在点A右侧的情况，忽视了点B在点A左侧的情况.本题应该分类讨论.为了更直观地观察点A，B的位置关系，我们不妨直接画出平面直角坐标系（如下页图3），以帮助我们思考.当点B在点A右侧时，其坐标是（3，2）;当点B在点A左侧时，其坐标是（-1，2）.

正解：填“（3，2）或（一1，2）”.

例4如图4，在平面直角坐标系中，第一次将△OAB变换成△OA 1B，，第二次将△OA1B1变换成△OA 282，第三次将△OA 282变换成……已知点A（1，3），A1（2，3），A2（4，3），B（2，O），B1（4，0），B2（8，0）.

观察每次变换前后三角形的变化规律，若将△OAB进行n次变换，得到△OAnBn，则点An的坐标为____，点Bn的坐标为_____.

错解：依次填“（2n，3）”“（2n+2，0）”，

解析：通过观察我们可以发现点A，A1，A2，A2，…，An都在平行于x轴的直线上，其纵坐标都为3，这些点的横坐标也有一定规律，即后面一个是相邻前面一个的2倍，点A1的横坐标可以记为2¹，点A2的横坐标可以记为2²，点A3的横坐标可以记为2³……点An的横坐标可以记为2“.点B，B1，B2，B3，…，Bn都在x轴上，其纵坐标都为0，它们的横坐标也有一定规律，后面一个是相邻前面一个的2倍，点B，的横坐标可以记为2²，点B2的横坐标可以记为23，点B3的横坐标可以记为2⁴……点Bn的横坐标可以记为2n+1.错解只是关注了点Bi的横坐标比点Ai的横坐标大2，可是再往后就不是这个规律了，例如点B2的横坐标比点A2的横坐标就大4，所以没有找对规律，

正解：依次填“（2n，3）”“（2n+1，0）”.

练一练

1.在平面直角坐标系中，若点P（a+1，a-1）在y轴上，则点P的坐标为——.

2.在平面直角坐标系中，已知点A（x，y），且xy=-2，点A在第____象限.

3.若建立一个平面直角坐标系，使点A的坐标是（-1，3），线段AB=5且AB平行于y轴，则点B的坐标是——.

4.在平面直角坐标系中，若点Q到x轴、y轴的距离分别是2，4，则点Q的坐标是__________.

5.如图5，矩形BCDE的各边分别平行于x轴或y轴.物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的邊运动.若物体甲按逆时针方向以1个单位长度，秒的速度匀速运动，物体乙按顺时针方向以2个单位长度，秒的速度匀速运动，则两个物体运动后的第2019次相遇地点的坐标是（

）.

A.（2，0）

B.（-1，1）

C.（-2，1）

D.（-1，一1）