探究圆锥曲线中一类定点问题
2023-11-30四川省名山中学625100高继浩
四川省名山中学(625100) 高继浩
一、试题呈现
题目(南通苏北部分学校2022 届高三四调) 已知为双曲线C的焦点,点P(2,-1)在C上.
(1)求C的方程;
(2)点A,B在C上,直线PA,PB与y轴分别相交于M,N两点,点Q在直线AB上,若证明:存在定点T,使得|QT|为定值.
解析易得试题第(1)问C的方程为= 1,下面解答第(2)问.设A(x1,y1),B(x2,y2),如图1,由易知直线AB的斜率存在,设其方程为y=kx+t,与双曲线方程联立,消去y得(1-k2)x2-2tkx-t2-3=0,则直线PA的方程为(x-2)-1,令x=0 得同理得yN=因为= 0,所以yM+yN=0,即整理得(2k-t+1)(x1+x2)-(2k+1)x1x2+4t=0,故2tk(2k-t+1)+(t2+3)(2k+1)+4t(1-k2)=0,化简整理得(t+3)(2k+t+1)=0.若t=-3,则直线AB过定点E(0,-3),由知PQ⊥EQ,令线段PE的中点为T(1,-2),则若t=-2k-1,则直线AB的程为y=k(x-2)-1,过定点P(2,-1),这不合题意.所以存在定点T(1,-2),使得
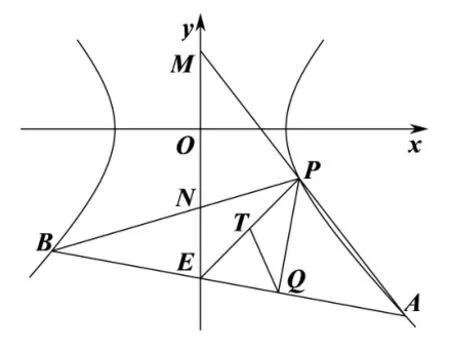
图1
二、推广探究
由试题解析可知直线AB过定点(0,-3),故该题的本质是定点问题,将双曲线方程和点P的坐标一般化,探究得到:命题1设点P(x0,y0)(y0̸=0),A,B在双曲线= 1(a>0,b>0) 上,直线PA,PB与y轴分别相交于M,N两点,若则直线AB过定点
证明由易知直线AB的斜率存在,设其方程为y=kx+t,与双曲线方程联立,消去y得(b2-a2k2)x2-2a2tkx-a2(b2+t2)= 0,设A(x1,y1),B(x2,y2),则
直线PA的方程为令x=0得同理得因为=0,所以yM+yN=0,即
整理得
故
若t=y0-x0k,则直线AB的方程为y=k(x-x0)+y0,过定点P(x0,y0),这不合条件.若则直线AB过定点所以直线AB过定点.
类似可得:
命题2设点P(x0,y0)(y0̸=0),A,B在双曲线上,直线PA,PB与x轴分别相交于M,N两点,若则直线AB过定点
三、类比探究
将命题1、命题2 类比到椭圆中,得到:
命题3设点P(x0,y0)(x0y0̸=0),A,B在椭圆上,直线PA,PB与y轴分别相交于M,N两点,若则直线AB过定点
命题4设点P(x0,y0)(x0y0̸=0),A,B在椭圆= 1(a>b>0) 上,直线PA,PB与x轴分别相交于M,N两点,若则直线AB过定点
命题2、命题3、命题4 的证明过程与命题1 类似,略.对抛物线进行探究,得到:
命题5设点P(x0,y0)(y0̸=0),A,B在抛物线y2=2px(p>0) 上,直线PA,PB与y轴分别相交于M,N两点,若
证明如图2,由则直线AB过定点易知直线AB的斜率存在,设其方程为y=kx+t,与抛物线方程联立,消去y得k2x2+2(tk-p)x+t2=0,设A(x1,y1),B(x2,y2),则x1+x2=x1x2=直线PA的方程为(x-x0)+y0,令x=0 得yM=同理得yN=因为所以yM+yN=0,即整理得
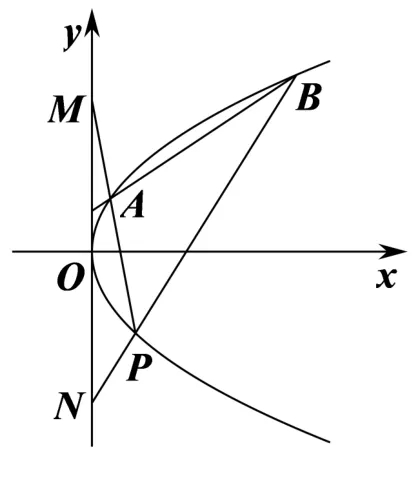
图2
故
化简得y0t2+(x0y0k-px0)t+px0(x0k-y0)=0,将px0=代入并分解因式得若t=y0-x0k,则直线AB的程为y=k(x-x0)+y0,过定点P(x0,y0),这不合条件.若则直线AB过定点所以直线AB过定点
