渗透美育，以美感人，引领教学

戴建峰

摘要：美育作为“五育并举”教育方针中的重要一环，可以有效唤起学生对宇宙、世界、自然的热爱，激发学生的创新灵感与学习数学的热情，借助高考，引领数学教学，合理培养学生良好的审美素养.

关键词：五育并举；高考；美育；简洁；对称；奇异；古典

从近年高考数学试题可以看出，命题切实落实“五育并举”的教育方针，引领数学教学与改革，一些涉及并充分体现德智体美劳等“五育”的考题均有出现，已经成为近年数学高考中的一道亮丽“风景线”.良好的审美素养影响着每个人对社会、他人及事物积极的人生态度，同时，良好的审美素养对人的全面发展及创造能力的培养等也十分重要.高考数学试题将对数学中的美育进行合理设置，唤起学生对宇宙、世界、自然的热爱，激发学生的创新灵感与学习数学的热情，引领并促进良好的审美素养的养成.

1 数学的简洁美

数学中的很多定义、定理、公式等都给人以简洁之美，精炼、清晰、和谐、统一，而在数学解题中，合理寻找、探索、欣赏、应用以及品味简洁优美的解法也给人以一种美的感受.

例1 〔2023年教育部新课标四省（云南、吉林、黑龙江、安徽）高考适应性考试数学试卷（2月）〕已知a，b，c满足a=log5（2b+3b），c=log3（5b-2b），则（）.

A.|a-c|≥|b-c|，|a-b|≥|b-c|

B.|a-c|≥|b-c|，|a-b|≤|b-c|

C.|a-c|≤|b-c|，|a-b|≥|b-c|

D.|a-c|≤|b-c|，|a-b|≤|b-c|

分析：直接利用题目条件，选取参数b的特殊值，结合代数式的关系与运算来确定对应的值，进而通过特殊值的比较与分析来加以合理判断，思路简洁，解题快捷.

解析：依题意，令b=2，则有a=log5（2b+3b）=log513，c=log3（5b-2b）=log321.

此时有ac-b>0，亦即|a-c|>|b-c|，可以排除选项C，D.

故选择答案：B.

点评：解决此类问题常用的方法就是严谨的推理与分析，而巧妙借助特殊值进行分析与判断，破解起来更为简洁快捷，判断起来效果更佳，方便易操作.特别在特殊值的选取上，有时还需要多次取特殊值来分析，突显特殊问题的简洁美，但无法完整解答所有满足条件的常数的取值情况.

2 数学的对称美

数学中的一些定义、公式、图形、关系式等都蕴含着极为丰富的对称美，如点（或中心）对称、直线（或轴）对称、对仗、对偶等，而在数学解题中，合理借助对称、对偶等极具对称美的数学知识，常常能发现一些具有事半功倍效果的优美解法.

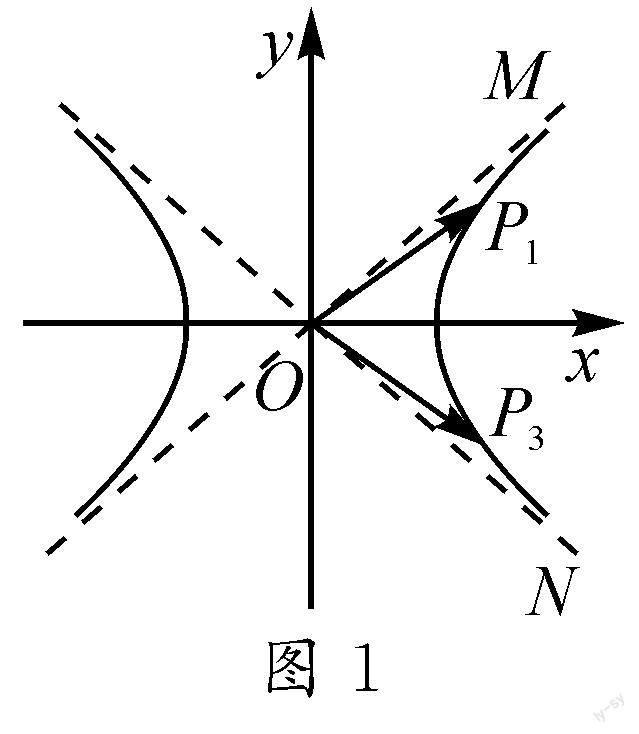
分析：根据题意，结合条件中对应的恒成立的不等式的结构特征，合理数学抽象，进行必要的类比与联想，化陌生为熟悉，转化为对应向量数量积的坐标关系式，利用双曲线的对称性质，构建图形，利用图形的直观性，通过平面向量的数量积以及双曲线的渐近线等相关知识来分析与处理.

解析：如图1，根据双曲线的对称性质，设点P2（x2，y2）关于x轴的对称点为P3（x2，-y2），则知点P3仍在双曲线的右支上.

所以实数a的取值范围为[1，+∞）.

故填答案：[1，+∞）.

点评：利用平面解析几何的相关知识与其他相关知识的交汇与融合，加以巧妙联想与合理类比等，通过题设条件及其对应的结构特征、几何意义等，综合数学中一些基本的概念或定义、基础知识、定理与公式等，利用对称点或对称思维，探寻对称的几何特征，展示数学的对称美.抓住关键，巧妙对称，合理转化，数形结合.

3 数学的奇异美

数学中的一些知识、结论或方法极具奇异性，出乎意料之外，又在情理之中，而在数学解题中，借助“之外”与“之中”之间的矛盾与统一，合理转化，跌宕起伏，情趣盎然，平凡之中，凸呈奇异.

分析：根据题目条件，利用极端思维，以特殊代替一般，结合动点P在椭圆C上（第一象限）运动时所带动的点Q，A，B等相关点的变化，取极端特殊情况——点A与B重合，利用特殊情况加以合理推理与分析，有效展示数学的奇异美，达到快捷分析与求解问题的目的.

解析：根据极端思维，取特殊情况，点A与B重合，此时B（a，0）.

故选择答案：D.

点评：借助极端思维中的极端位置法处理，以特殊位置代替一般位置，合理交汇“动”与“静”的联系与变换，化一般情况为特殊情况，从而借助数学中的奇异思维来解决一般性问题，奇异完美，合理巧妙，简单快捷.

4 数学的古典美

数学具有悠久的历史，而数学文化类试题又是近年高考的热点之一，经常结合数学文化或现实生活中的问题背景进行创新情境设置.在数学解题中，充分利用数学知识、思想或方法来诠释其古典美，挖掘内涵，体会美感.

例4 （2023届江苏省苏北七市一模数学试卷）2022年神舟接力腾飞，中国空间站全面建成，我们的“太空之家”遨游苍穹.太空中飞船与空间站的对接，需要经过多次变轨.某飞船升空后的初始运行轨道是以地球的中心为一个焦点的椭圆，其远地点（长轴端点中离地面最远的点）距地面S1，近地点（长轴端点中离地面最近的点）距地面S2，地球的半径为R，则该椭圆的短轴长为（）.

分析：根据题设条件，结合数学文化与空间知识的创新设置，通过对远地点与近地点对应概念的理解，结合椭圆中相关参数之间的关系，合理转化与应用，进而得以确定椭圆的短轴长问题，在此过程中借助数学建模充分展示数学的古典美.

解析：依题可知a+c=S1+R，a-c=S2+R.

故选择答案：D.

点评：此类以圆锥曲线中的椭圆等为基本场景创设的数学文化问题，巧妙融入神舟飞船的应用场景，借助數学知识与美育教育加以交汇融合，科学数学建模，利用椭圆中相关要素之间的关系，合理构建关系式是解决问题的重要之处，倡导数学应用与数学美感.

“世界不缺乏美，而是缺乏对美的发现”，数学也一样不缺乏美，数学美数不胜数.

高考作为我国教育体系的一个重要环节，必须切实服务于我国教育坚持“一核引领”（立德树人），倡导“五育并举”（德智体美劳）的根本目标.借助美育渗透，以美感人，命制与核心考点相关联的数学题目，体现数学的应用性和创新性，强调理性思维，突出数学应用，引领数学教学与数学学习，意在全面考查学生数学能力，培养学生数学核心素养.