正交于顶，隐含定点

黄轶

摘要：基于一道涉及抛物线的教材习题，追根溯源，通过对问题的反思，合理逆向思维，类比拓展，总结规律.结合逻辑推理与数学运算，得到抛物线中过定点两弦相关斜率代数关系式为定值背景下的一些优美结论，拓展学生思维，提升数学能力，培养数学核心素养．

关键词：抛物线；教材；类比；斜率；拓展

数学家波利亚曾说：“一个认真备课的教师能够拿出一个有意义但又不太复杂的题目，去帮助学生发展问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域．”［1］特别地，教材中的一些典型的例题或习题，其背景深刻，知识丰富，典型性高，拓展性强，蕴含丰富的数学思想方法，如果有针对性地加以利用，有思想性地引导，有方向性地探究，有思维性地拓展，则可以全面提升学生的数学品质，提高数学能力，培养数学核心素养［2］．

1 源于教材

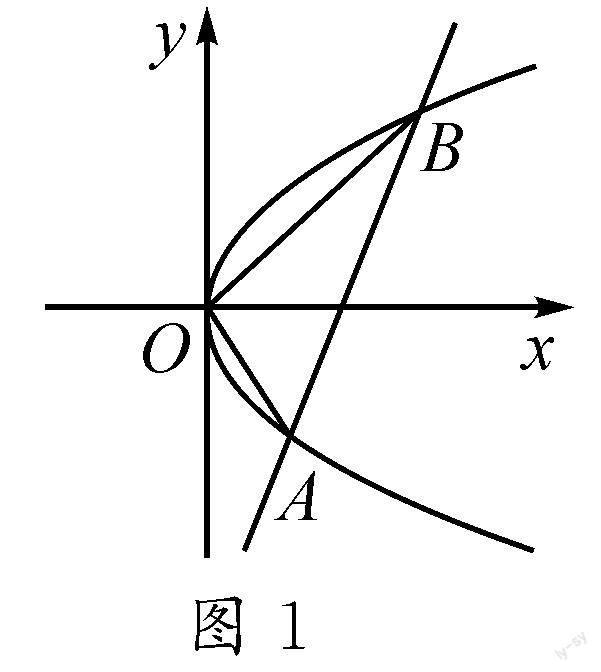
例题 〔人教版《数学》（选择性必修第一册）3.3抛物线第138页第6题〕如图1，直线y=x－2与抛物线y2=2x相交于A，B两点，求证：OA⊥OB．

设A（x1，y1），B（x2，y2），则y1y2=－4.

故OA⊥OB．

反思：根据抛物线关于对称轴的对称性，将上述例题中的直线“y=x－2”替换成直线“y=2－x”（两直线的图象关于x轴对称），同样可得结论OA⊥OB．而直线y=x－2与直线y=2－x有公共点（2，0），结合抛物线y2=2x可知2p=2，那么直线y=x-2过点（2，0）与OA⊥OB之间是否存在某种特殊的联系呢？

2类比拓展

以上问题的实质就是抛物线的弦对顶点张直角的相关性质（抛物线的弦对顶点张直角时恒过定点）．借助逻辑推理、思维拓展、类比提升等，可以对抛物线过顶点（或其他定点）的两弦斜率之积、斜率之和、斜率倒数之和等为定值的相关结论，进一步加以归纳、推广与总结．

2.1 抛物线过顶点两弦斜率之积为定值

结论1 已知A，B为抛物线y2=2px（p>0）上两动点，O为坐标原点.若OA⊥OB，则直线AB恒过定点（2p，0）．

证明：设A（x1，y1），B（x2，y2），直线AB的方程为x=my+t.

因此，对于上述教材中的习题，因为抛物线y2=2x中的p=1，并且直线y=x－2经过点（2，0），所以有OA⊥OB成立．

结论1是其推广的特例，是当常数SymbollA@=－1时的结果．

推广的证明可参照结论1的证明加以分析与处理，这里不多赘述．

2.2 抛物线过定点两弦斜率之积为定值

结论2 已知A，B为抛物线y2=2px（p>0）上两动点，P（x0，y0）为抛物线上一定点，且满足PA⊥PB，则直线AB恒过定点（2p+x0，－y0）．

证明：设A（x1，y1），B（x2，y2）.

（y20－y21）（y20－y22）+4p2（y0－y1）（y0－y2）=0.

整理可得（y0+y1）（y0+y2）=－4p2，则有y1y2=－4p2－（y1+y2）y0－y20=－4p2－（y1+y2）y0－2px0.

由此可知，直线AB恒过定点（2p+x0，－y0）.

经检验，当x1=x2时，也满足.

因此，直线AB恒过定点（2p+x0，－y0）．

2.3 抛物线过定点两弦斜率之和为定值

证明：设A（x1，y1），B（x2，y2），直线AB的方程为x=my+t.

推廣 已知A，B为抛物线y2=2px（p>0）上两

2.4 抛物线过定点两弦斜率倒数之和为定值

证明：设A（x1，y1），B（x2，y2），直线AB的方程为x=my+t.

y2－2pmy－2pt=0.

由韦达定理，可得y1+y2=2pm.

3 教学启示

上文中以一道课本习题为源，得到抛物线中过定点的两弦斜率之积、斜率之和、斜率倒数之和为定值条件下的相应的优美结论，合理反思总结，拓展思维，总结规律，构建全面的逻辑思维体系与应用．

事实上，抛物线中的相关结论及其推广，还可以进一步拓展到圆锥曲线中去，有关圆锥曲线斜率之积（或之和、倒数之和）为定值的问题层出不穷．当我们站在系统的高度，合理地整合知识，很多时候都能有一个思维方向，避免进入无头绪的计算误区，全面提升能力，养成思维习惯，培养数学核心素养．

参考文献：

［1］江南岸.改进解题教学 提升复习效益——高三复习解题教学策略例谈［J］.上海中学数学，2020（10）：4-7，17.

［2］蒋自佳.基于问题驱动的一类定点定值问题探究［J］.高中数学教与学，2022（13）：13-16.