支架式教学在高中数学教学中的应用
2023-11-25袁美玉房维维
袁美玉 房维维


摘要:本文中首先介绍了支架式教学的内涵及过程,然后结合人教A版选择性必修第三册第七章第五节“正态分布”的教学案例,分析如何在教学中利用支架式教学模式,以达到引导学生体会知识的生成过程,理解知识的本质,提高问题解决能力,提升核心素养的目的.
关键词:支架式教学;正态分布;教学设计
支架式教学是以学习者为中心,以培养学生的问题解决能力和自主学习能力为目标的教学模式.教师向学习者提供一些线索和提示,引导学生发现和解决学习中的问题,掌握所要学习的知识,提高问题解决能力,培养学生成长为独立的学习者.
合理利用支架式教學能有效培养学生自主学习能力和解决问题的能力,支架式教学正逐渐被高中数学教师所采用.笔者以人教A版“正态分布”的教学设计为例,探讨如何在教学中合理利用支架式教学实现其应有的价值.
1 “正态分布”教学设计思路
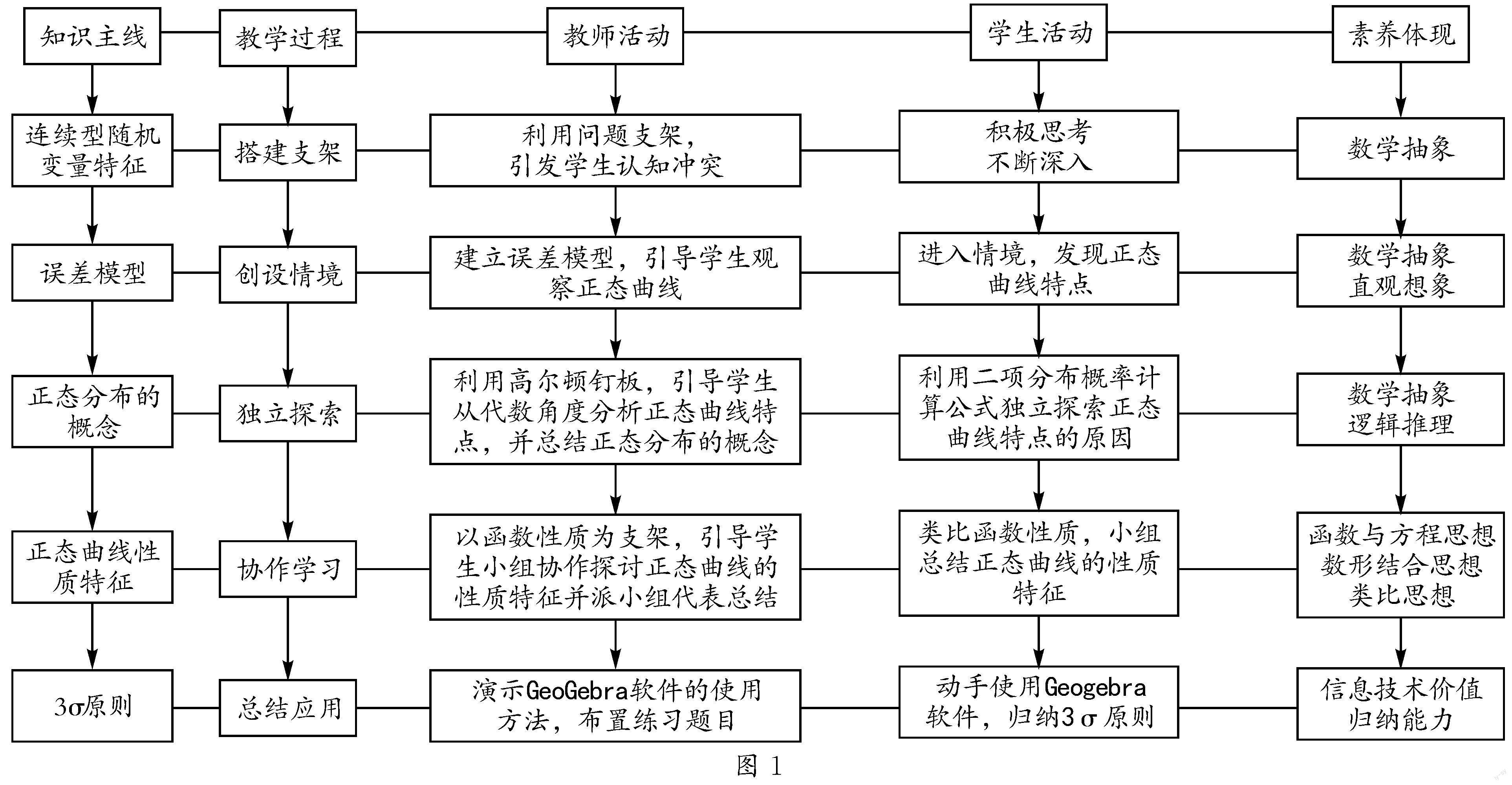
本节课选自2019年人教A版高中数学选择性必修第三册第七章《随机变量及其分布列》第五节,教学素材丰富,可以很好地利用情境支架、问题支架、工具支架、实验支架、数学文化等多个支架层层递进地进行教学设计.结合本节课的教学内容设计教学思路如图1所示.
2 “正态分布”教学设计
环节1:搭建概念支架,明晰连续型随机变量特征
【问题支架1】师:在生活中存在着大量的随机事件,比如在学校内任意选取一名同学,我们能否事先准确地猜测出这位同学的身高?
【问题支架2】师:这位同学身高的可能取值你能列举出来吗?如果能,请列出它的分布列.
追问:该同学身高正好为1.70 m的概率是多少?
师生总结:总结连续型随机变量的主要特征并与离散型随机变量进行对比学习.
设计意图:根据两个问题支架,引发学生的认知冲突,同化学生原有的认知结构.
环节2:创设情境支架,建立误差模型,观察曲线特点
【情境支架】师:某钢材厂生产了一批钢筋,为了检验钢筋长度是否符合出厂标准,随机抽取出了1 000根钢筋,计算误差,并且绘制频率分布直方图和折线图.
【工具支架1】利用几何画板动态展示直方图组距逐渐缩小的过程(可通过图2扫码观看).
学生总结:随着组距减小,频率分布折线图近似于一条光滑的曲线,这条曲线会有中间高、两边低、左右大致对称的特点.
【问题支架3】师:这种特点只是该随机变量所特有的吗?它是偶然的现象吗?
设计意图:激发学生的学习兴趣,引导学生进一步探究曲线有“中间高、两边低、左右对称”特点的原因.
环节3:深入探究正态曲线特点的原因
【实验支架】教师介绍高尔顿钉板的结构.
【问题支架4】小球下落的位置是一个随机事件吗?
追问1:大量的小球下落,它的分布会不会呈现特殊的规律呢?
追问2:多次实验,结果还是一样的吗?
【问题支架5】为什么随机变量的概率分布会呈现这样的特点呢?(提示:高尔顿钉板曾在学习二项分布时有过应用.)
在生活中,众多的、互不干扰的、不分主次的偶然因素所作用而产生的连续型随机变量,例如某些物理量的测量误差,某地每年某月的平均降水量、平均气温,某一地区同年龄人的身高、体重等都服从正态分布.
环节4:小组协作学习,探索正态曲线的性质特征
【问题支架6】依据函数的性质,分析正态密度函数解析式和正态曲线,总结正态曲线的性质特征.(小组合作,并派小组代表汇报本组的研究成果.)
追问1:在学习函数的过程中,我们通常学习函数的哪些性质?
追问2:正态密度函数的定义域是什么?值域是什么?
追问3:正态密度函数有怎样的单调性?
追问4:正态密度函数的对称轴是什么?
追问5:函数的最大值在何处取得?
设计意图:从正态密度函数解析式入手,不仅可以准确地分析正态曲线的性质特征,还可以提高学生分析函数解析式的能力.
【问题支架7】利用几何画板,观察当μ和σ分别发生改变时,见图4、5,正态曲线有怎样的变化规律?这两个参数在统计学中有何意义?(可通过图3扫码观看.)
学生总结:参数μ反映了正态分布的集中位置,σ反映了随机变量的分布相对于均值μ的离散程度.
教师总结:在实际问题中,参数μ,σ可以分别用样本均值和样本标准差来估计,所以
若X~N(μ,σ2),则E(X)=μ,D(X)=σ2.
【问题支架8】对于服从正态分布的随机变量,如何求得随机变量的取值落在某个区间内的概率?
追问:正态曲线与x轴围成的面积是多少?
环节5:应用GeoGebra软件,归纳3σ原则
【工具支架2】师:正态密度函数可以由μ,σ两个参数唯一确定,假设X~N(0,1),可以利用
GeoGebra软件,求得随机变量的取值落在任意区间内的概率,如图6所示.
引导学生在练习操作GeoGebra软件的过程中自主总结出3σ原则.
学生总结:假设X~N(μ,σ2),则
P(μ-σ≤X≤μ+σ)≈0.682 7;
P(μ-2σ≤X≤μ+2σ)≈0.954 5;
P(μ-3σ≤X≤μ+3σ)≈0.997 3.
教师总结:尽管正态变量的取值范围是实数集,但是取值落在区间[μ-3σ,μ+3σ]以外的概率大约只有0.002 7,通常认为这种情况几乎不可能发生.所以在实际应用中,通常认为服从正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
3 总结与反思
本设计的亮点之一在于在教学过程中,真正做到了以教师为主导,以学生为主体.通过一个个支架,引导学生向上攀升,逐渐提升解决问题的能力.
亮点之二在于教师提供函数性质这一支架,类比函数的性质,学生自主发现了正态曲线的性质特征.通过小组交流,学生现场产生头脑风暴,互相补充,总结出结论.既锻炼了学生通过类比迁移知识的能力,又提高了学生协作交流的能力.
亮点之三在于教师演示了GeoGebra软件的使用过程之后,学生有机会实践操作,并且了解到对于服从正态分布的随机变量,只需要知道样本的均值和标准差,就可以求得随机变量的取值落在某区间内的概率.体会正态分布的无穷魅力.
不足之处在于在正态分布模型的教学中应该培养学生数据分析观念和数学建模能力.由于课堂时间有限、样本容量有限,因此未能展开对学生生活中服从正态分布的随机变量进行数据收集的工作,弱化了对学生数据分析观念和数学建模能力的培养.
