设计“一题一课” 促进中考复习

费云标

［摘  要］ 文章以2020年南京中考数学第26题为基础，设计“一题一课”的中考复习课，帮助学生形成解析几何的思考路径，积累解题经验，提升解题能力.

［关键词］ 一题一课；中考；复习课

案例的背景

本节课源于笔者参加的区内的一次教学案例设计比赛，现基于“一题一课”模式设计成中考复习课，促进自身的专业成长. 本节课的教学关键是添加辅助线来构造相似三角形.

学生在“九下”已经学习了相似三角形的概念、性质、判定和简单应用，以及图形的平移、对称、旋转等变化. 本年级组的学生已经掌握了相关的基础知识与基本图形，但对相似三角形的综合运用还相对薄弱，自主建构模型的能力不强. 因此，通过学生熟悉的教材习题作为前测唤醒其基本知识、基本技能、基本解题经验，以2020年南京数学中考第26题为例引发学生再思考相似三角形的性质与判定，让学生亲历解题过程，找到题眼与关键，暴露思维，及时反思，积累解题经验，提升解题能力. 通过设计问题串促进学生深度学习，反思解题路径，优化解题思维.

教学过程

环节1：回归教材，先行组织

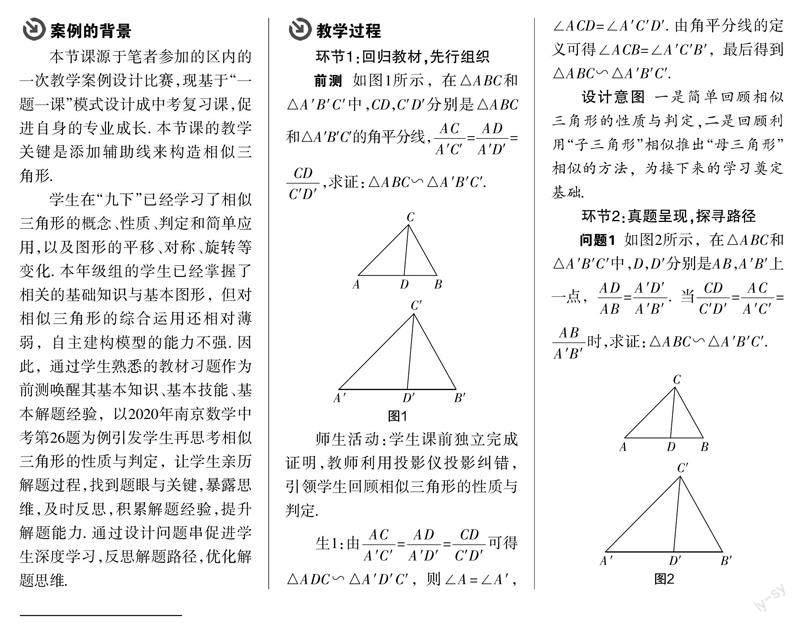
前测  如图1所示，在△ABC和△A′B′C′中，CD，C′D′分别是△ABC和△A′B′C′的角平分线，==，求证：△ABC∽△A′B′C′.

师生活动：学生课前独立完成证明，教师利用投影仪投影纠错，引领学生回顾相似三角形的性质与判定.

生1：由==可得△ADC∽△A′D′C′，则∠A=∠A′，∠ACD=∠A′C′D′. 由角平分线的定义可得∠ACB=∠A′C′B′，最后得到△ABC∽△A′B′C′.

设计意图  一是简单回顾相似三角形的性质与判定，二是回顾利用“子三角形”相似推出“母三角形”相似的方法，为接下来的学习奠定基础.

环节2：真题呈现，探寻路径

问题1  如图2所示，在△ABC和△A′B′C′中，D，D′分别是AB，A′B′上一点，=.当==时，求证：△ABC∽△A′B′C′.

师生活动：教师借助多媒体展示问题1，学生先独立解题，再展示解法. 教师利用框图引导学生整理证明思路.

生2：我发现条件之间有联系，先将=变形为=，再结合条件==，可得===，从而推出△ADC∽△A′D′C′，得到∠A=∠A′，最后根据“两边成比例且夹角相等的两个三角形相似”得△ABC∽△A′B′C′.

设计意图  学生亲历解题过程，回顾比例的性质、相似三角形的性质与判定.

追问1  请你利用框图（见图3）来梳理你的证明思路.

师生活动：学生阅读框图并填写框图，整理思路后由教师点评.

生3：我填写的是“==”和“∠A=∠A′”. 我是利用逆向思维的方式从△ABC∽△A′B′C′去推导的，只要找到能够串联信息的“桥梁”就可以了.

设计意图  学生填写框图这一过程体现了分析与综合思维方式，为下一题的解答思路提供了活动经验.

追问2  回顾解题过程，说一说如何分析本题.

师：分析问题可以从条件出发，也可以从结论出发，找到中间结论，再找到两者间的桥梁. 我们发现本题中两者間的桥梁就是“子三角形”相似.

设计意图  回顾此题的解答思路，即寻找“子三角形”相似，也为下一题的解答思路奠定了基础.

环节3：变式探究，素养提升

问题2  如图4所示，在△ABC和△A′B′C′中，D，D′分别是AB，A′B′上一点，=. 若==，请判断△ABC与△A′B′C′是否相似，并说明理由.

师生活动：教师借助多媒体展示题目，学生先自主探究，大胆猜想△ABC与△A′B′C′相似. 针对学生的猜想，教师提出问题：如何证明这两个三角形相似？沿用问题1的解答经验与方法，学生分析易证的结论（=，=，=，==），同时联想须知的条件（∠ACB=∠A′C′B′或==）. 但由于学生无法直接证明△ABC与△A′B′C′相似，因此教师继续问道：能够证明图中的“子三角形”相似吗？学生依然无法直接证明△ACD与△A′C′D′、△BCD与△B′C′D′相似，于是教师通过追问引导学生强化条件来解题.

设计意图  综合分析已知、易证和须知的条件，大胆尝试方案，再小心求证，明确解题方向.

追问1  为联通已知条件=与==，你打算怎么做？

师生活动：学生自主探索，先画一画，再进行小组交流，展示辅助线.  教师引导学生思考画辅助线的依据. 学生从线段成比例联想作辅助线，或从相似的基本图形联想作辅助线，如有学生作平行线构造A型相似或X型相似，还有学生构造其他类型（如作高、角平分线或中线）. 教师单独指导，让学生试一试证明；巡视指导，让学生选择一种有利于联通已知条件=与==的方法，并展示相应的构造辅助线的方案，然后挑选其中一种进一步探究.

设计意图  学生先独立作图，然后小组讨论其合理性. 从数与图两个角度出发，教师组织学生思考作图依据，再选择方案展示逻辑推理. 既聚焦生成，也贴合学情，更促进学生深度学习，有效突破难点.

生4（A组代表）：如图5所示，过D作DE∥BC交AC于E，过D′作D′E′∥B′C′交A′C′于E′.

追问2  你还能得到什么结论？

师生活动：学生独立思考，猜想△CDE与△C′D′E′相似. 教师追问：如何判定它们相似？如何证明==？通过追问，学生得到结论：====. 教师肯定结论后继续问道：你还能得到什么？学生继续探究得到=====. 教师又追问：你如何证明==？还有其他推导方法吗？学生分享解法，投影展示. 教师指出：既可以用比例的性质（合比性质、分比性质、等比性质）来解决，还可以设线段的长度（比如设k）直接证明，，的值相等来解决.

设计意图  学生通过已知推可知的过程，就是优化方案的过程. 此题的价值在于不仅帮助学生找到了证明三角形相似的条件，还展示了线段成比例的证明方法，有效突破了本节课的难点.

追问3  现在可以证明△ABC与△A′B′C相似吗？请你完成证明过程.

师生活动：学生完成证明过程，并互助点评，明确几何证明书写规范.

设计意图  通过展示证明过程，提出证明规范要求，提高学生的解题规范意识.

追问4  还有不同的解法吗？简要说明证明思路. 请你对这些解法作点评.

师生活动：小组交流，扩充解法. 学生讲解，同伴点评，优化思考.

设计意图  通过相似的基本图形来作辅助线，形式多样，辅助线的作用相同. 说明证明思路，有利于学生了解此类题目的解法实质就是寻找“子三角形”相似，积累学生的解题经验，提高学生的解题能力.

追问5  回顾以上解决问题的过程，你能说一说解决较复杂的几何证明题的思考路径吗？

思考路径如图6所示.

设计意图  教师整理学生的发言，引领学生总结梳理，形成几何证明题一般的解决套路，帮助学生养成系统整理知识的习惯，提升学生的解题能力，发展学生的核心素养.

环节4：回顾小结，布置作业

回顾小结：请你回顾一下本节课的学习过程，谈一谈你的学习感想.

师生活动：教师带领学生回顾学习过程，提炼总结. 学生回顾基础知识：平行线分线段成比例，相似三角形的判定与性质，相似的基本图形；回顾辅助线的作法：综合分析已知、可知、须知、未知，结合基本图形作辅助线；还回顾线段成比例的证明方法：比例的性质，设线段的长度（设k）. 积累较复杂的几何问题的解决经验：从条件出发，从结论出发，从强化条件出发，从合情推理出发，等等.

设计意图  通过开放式问题，让每一个学生能说出自己的收获，引导学生从基本知识、基本技能、基本解题经验、基本思想方法等不同方面对本节课进行反思、梳理，有助于学生积累相关数学问题的解决经验.

布置作业：

题1：如图7所示，在△ABC和△A′B′C′中，D，D′分别是AB，A′B′上一点，=.若==，求证：△ABC∽△A′B′C′.

设计意图  考查相似三角形的判定与性质，利用“子三角形”相似推出“母三角形”相似.

题2：如图8所示，在△ABC和△A′B′C′中，D，D′分别是AB，A′B′上一点，=.当=，∠A=∠A′时，判断△ABC与△A′B′C′是否相似. 若相似，请说明理由；若不相似，请画出反例图形.

设计意图  考查相似三角形的判定与性质，并结合作图来举反例.

对教学设计的反思

本节课以2020年南京中考数学第26题为基础，设计成“一题一课”的课型；通过教材溯源，再变式探究，完成解题教学. 从而帮助学生形成解决相似证明题的思考路径，积累解题经验，提升解题能力.

1. 选取有价值的问题，让教学更高效

选取有价值的问题是“一题一课”习题教学的关键. 教师应当基于课程标准，把握学情、教材与中考，选择学生遇到的典型习题或测试题作为“一题一课”的主要问题素材，再设计一系列的问题生长为一节课. 本节课选择的是2020年南京中考数学第26题. 首先从知识层面来看，本題考查的是比例的性质、相似三角形的性质与判定等知识. 其次从能力层面来看，本题考查学生的逻辑推理、代数推理、几何直观等综合能力. 再次从数学思想方法来看，构造辅助线的方法，可以从“数”（比例）的角度来研究“形”（形状、大小），联想到作平行线，构造相似的基本图形（A型或X型相似），体现了数形结合思想. 最后从解法策略来看，问题1以框图的形式表达对证明路径的思考，呈现方式简洁明了，思维可见；问题2的辅助线的作法多样，如A型相似、X型相似，同一作法不同角度求解（一题多解），以提升学生的几何推理能力，发展学生的核心素养.

2. 关注教学生成，让教学更时效

布鲁纳认为，学习知识的最佳方式是发现学习. 发现学习指学生利用教材或教学资源自己独立思考，自主发现知识，掌握原理和规律的过程. 在本节课中，笔者始终关注学生的学习心理，比如，前测习题选自教材，让学生先完成，互相纠错，从而发现问题、铺垫思路. 又如，在问题1的探究环节中，笔者给予学生足够的时间去交流，让学生的思维充分碰撞，使其获得一般的证明方法. 再如，在问题2的探究过程中，笔者通过开放式问题的设计，让学生优化思考，搭建中介条件，最后指向辅助线求解. 不仅给予学生再发现的机会，还激发学生挑战自己的勇气，在试错的过程中加深学生对新知识的理解与内化.

3. 关注深度学习，让教学更高效

深度学习不仅体现在思考的深度上，还体现在思考的广度上. 笔者认为，浅层思考多个问题不如深度思考一个问题. 在本节课中，笔者践行着深度学习的流程及标准，比如，在问题2的探究过程中，笔者提出了一连串问题：如何证明这两个三角形相似？能够证明图中的“子三角形”相似吗？如何联通已知条件=与==？你打算如何作辅助线？层层追问指向运用辅助线构造“子三角形”相似，为学生归纳相似证明题的基本解决思路做准备. 当学生解决完此题后，又追问道：还有不同的解法吗？简要说明证明思路. 请你对这些解法作点评. 从而让学生弄清运用“子相似”证明“母相似”的思路，有利于培养学生的迁移能力与思考广度. 再如，作业题2是变式训练，让学生涉猎此类问题，有助于开拓学生的视野，发展学生的几何想象能力.

结束语

在数学课堂上，教师应让学生真正有效地经历认知过程，让他们感受到数学是有活力的，其充满着有趣的问题和新的思考方式，以激发学生学习更多东西的欲望，更好地培养他们的数学学习能力，使他们慢慢养成一种积极的学习习惯. 一旦学生具备了这样的主动性，他们的数学素养就能切实提高.

每一个学生都有获得数学素养的需求与能力，开始时的表达效果可能还不是最终的素养体现，但是笔者相信，数学教学的主要目的是培养学生的数学思考能力，并帮助其转换成数学核心素养，从教师灵巧的教学设计开始，让数学素养落地生根.