让中华优秀传统文化融入高中数学课堂

王佳敏　张维忠

摘要：以“祖暅原理与球体体积”为例，将中华优秀传统文化融入高中数学课堂，教师可以从刘徽的“牟合方盖”出发，引入祖暅原理，引导学生推导球体体积公式，并继续探索椭球体体积，让学生探索数学知识本质，培养学生的创造性思维与民族自豪感，进一步增强学生的文化自信。

关键词：中华优秀传统文化；高中数学；祖暅原理；球体体积

中华优秀传统文化源远流长、历久弥新，在当今社会有着独特的育人价值。而数学文化作为中华优秀传统文化的重要组成部分，对人的发展有着不可替代的作用。无论是中国古代数学家创造的数学成果、积累的思想方法还是其坚持不懈的探究精神，都可以促进学生发展。在数学学科教育教学过程中渗透中华优秀传统文化，让学生感悟前人智慧，可以培养学生的民族自豪感，增强学生的文化自信，对学生全面发展有着不可替代的作用。本文以祖暅原理为例，探究如何将中华优秀传统文化融入高中数学课堂。

祖暅原理作为中国古代数学研究的重要成果，是伴随着球体体积问题而产生的，因此在球体体积公式推导过程中引入祖暅原理，可以促进学生对公式的理解。在以往球体体积教学过程中，不少教师会直接给出公式，或把祖暅原理作为了解性阅读材料，学生对公式死记硬背，没有深层次的理解，课堂也显得枯燥无味。因此，也有不少教师进行探究，有探究祖暅原理从而推导球体体积公式的，还有深入探究祖暅原理并把球体体积公式作为课后探究作业的。但是，大部分研究都止步于球体体积公式。作为中华优秀传统文化的祖暅原理有着更深远的教育价值，教师应当引导学生深入了解其思想，再通过类比推理探索其他几何体体积的计算方法。基于此，本文借助信息技术，从刘徽的“牟合方盖”出发，引入祖暅原理，意在引导学生推导球体体积公式，并继续探索椭球体体积，让学生探索数学知识本质，培养学生的创造性思维与民族自豪感，增强文化自信。

一、教学内容分析

（一）教材分析

本节课是人教A版普通高中数学教材必修二中第8.3.2节“圆柱、圆锥、圆台、球的表面积和体积”与“探索与发现”中“祖暅原理与柱体、锥体的体积”的整合。教材给出的祖暅原理仅作为阅读性材料，学生难以真正理解背后所蕴含的数学知识与原理，也难以进行应用拓展。为此，需要教师分析、补充教材内容，并在教学环节进行渗透。

（二）学情分析

授课对象是高一学生，他们已经学习过旋转体、棱锥、球体的概念和棱锥体积计算公式，为本节课学习奠定了基础。本节课内容从刘徽的“牟合方盖”出发，引入祖暅原理，引导学生进行探究，进而推导出球体体积公式，对学生的空间想象能力、逻辑推理能力和計算能力都提出了要求。

（三）教学重难点分析

教学重点：理解祖暅原理的涵义，培养学生空间想象能力。

教学难点：运用祖暅原理推导球体体积公式，通过类比推导椭球体体积公式。

二、教学设计

（一）回顾旧知，文化融入

师：同学们还记得棱锥与圆锥的体积公式吗？

师：同学们是否感受到这两个公式有相似之处？请带着这个问题一起来学习球体体积公式。今天，我们将和中国古代数学家一起探究球体体积公式。第一位中国古代数学家是刘徽，他对《九章算术》做注释时发现球体体积公式有误，从而开始探求球体体积公式。为了解决这个问题，他创造了“牟合方盖”。什么是“牟合方盖”呢？同学们看老师手里的两根粉笔，如果一根粉笔能穿过另一根粉笔，这两根粉笔交叉重合的部分就叫“牟合方盖”，释义为两把对合的方伞。请动手操作，并尝试画出“牟合方盖”的图象。

教师利用信息技术演示，并得到“牟合方盖”的图象（见图1、图2）。

师：我们可以观察到图1中的“牟合方盖”并不是球体，但为什么能通过计算“牟合方盖”体积得到球体体积呢？同学们先来找一找“牟合方盖”中的球体。

生：图2中两个半径相同的圆柱垂直交叉，可以找到内切于“牟合方盖”的球体。

教师利用信息技术演示，画出“牟合方盖”中的内切球。

师：刘徽在球体的外切立方体中作两个垂直相交的内切圆柱得到“牟合方盖”。假设球体半径是r，如果在任意高度用水平面截“牟合方盖”，会得到什么图形？

生：正方形。因为圆柱侧面截图是一个矩形，这个两个圆柱半径相同，所以是正方形（见图3）。

师：那用水平面同时截“牟合方盖”和内切球是什么图形？

生：正方形与内切圆。

【设计意图】首先，回顾已学习棱锥与圆锥的知识，再引入刘徽的“牟合方盖”，为学生理解祖暅原理做铺垫。其次，对于“牟合方盖”，学生直接想象存在困难，因此教师让学生动手操作，观察并尝试画图，再适时借用信息技术演示，突破学生认知障碍，加深学生印象。再次，内切球和“牟合方盖”体积通过推导计算得到而不是直接给出，有助于学生理解数学知识产生的过程。最后，教师介绍刘徽和祖暅的故事，展示中国古代数学家实事求是、坚持不懈的精神。

（二）合作探究，文化理解

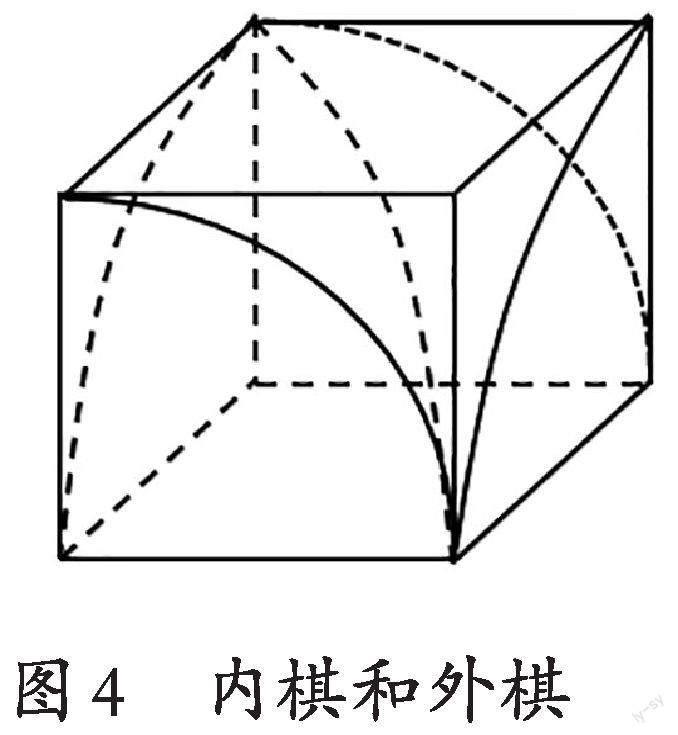
师：祖暅在推导球体体积时沿袭了刘徽的思想方法，把“牟合方盖”分成了八个相同的图形。他将“牟合方盖”的部分称为内棋，外部称为外棋，并将外棋划分为三块，同学们能否画出三块外棋？

教师给学生思考时间，鼓励学生画出图形（见图4）。教师利用信息技术将外棋部分进行演示（见图5）。

师：在计算外棋体积时，祖暅提出一条很重要的原理“幂势既同，则积不容异”，称为祖暅原理。意思是夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等。同学们能否依据今天所学的知识来理解祖暅原理？

师：利用祖暅原理能否解决一开始棱锥与圆锥体积公式的问题？

生：连接三条线段，形成的棱锥满足条件（见图6）。

【设计意图】首先，教师从整体出发分析和解读祖暅原理，再结合刘徽的内切球和“牟合方盖”体积比值推导过程进一步理解祖暅原理。其次，学生的空间观念较为薄弱，教师让学生动手操作，再借助信息技术分割外棋，加深学生对外棋的理解，培养学生的空间想象能力。最后，教师利用祖暅原理推导出球体体积公式，让学生掌握研究几何体体积求解的基本思路，提高学生逻辑推理能力。

（三）类比推理，文化拓展

师：球体是圆绕直径旋转而得。现考虑椭圆，设较长的轴为2a，较短的轴为2b，面积为πab，求绕较长轴旋转形成的椭球体体积公式。请同学们对比圆与椭圆，先来猜测椭球体体积公式。

师：由此证明同学的猜想是正确的。我们可以大胆猜想，但猜想的结果是否正确还需要经过严格的论证。

【设计意图】教师鼓励学生从已有经验去推理未曾经历过的东西，从而激发学生好奇心和深入学习的热情，并启发学生思考如何在知识间建立联系，从而把握数学知识本质。圆与椭圆有相似之处，学生先通过类比方法猜想椭球体体积，再严密推导计算验证答案，巩固了刘徽的思想方法与祖暅原理的知识，不仅体验了数学知识发生发展的过程，还培养了创造性思维。

（四）归纳总结，文化体悟

师：同学们通过今天这节课有什么收获？

生：学习了祖暅原理，被平行于这两个平面的任意平面所截，如果截面面积总相等，那么这两个几何体体积相等。还由祖暅原理推导出球体体积公式。

师：同学们从中国古代数学家身上学到了什么？

生：书本知识也会出错，刘徽发现了《九章算术》上的错误。

生：任何时候都不能放弃探究，虽然刘徽没有得到正确答案，但是正因为他的努力，祖暅才能在其基础上得到正确答案。

教师对学生的回答予以肯定，鼓励学生质疑思辨，课后继续探索。

教师布置课后作业：搜集整理祖暅原理还能解决哪些问题，并尝试推导和解决；思考还有什么方法可以推导出球体体积公式。

【设计意图】通过讨论，教师引导学生回顾本节课中用到的知识和思想方法。虽然学生的回答各不相同，但是答案合理即可，重在让学生体验中国古代数学家的智慧与感受他们坚持不懈的精神。

三、启示与思考

（一）以数学文化育人，发展数学核心素养

中华优秀传统文化是培养数学核心素养的最佳素材之一。一方面，教师应引导学生重构中国古代数学家的探究过程，理解知识发生、发展过程，并最终应用知识解决问题，这也是促进学生数学核心素养发展的过程。无论是探究刘徽的“牟合方盖”，还是应用祖暅原理推导球体体积，都对学生的空间想象能力提出较高的要求，教师需要把握时机，培养学生的空间想象能力。另一方面，教师可以将中华优秀传统文化融入高中数学课堂，通过介绍刘徽的坚持不懈探求，让学生感受到数学家求真务实的科学精神与严谨的治学态度。教师介绍祖暅原理是伴随球体体积问题而产生的，可以让学生感受数学在实际生活中的应用与价值，感受中国古代数学家的智慧，培养积极的数学品格与数学价值观念。

（二）用文化搭建桥梁，展现数学知识本质

中华优秀传统文化可以成为沟通学生经验与数学本质之间的桥梁。教师如果没有意识到数学知识是数学文化的基础，并过多使用了解性阅读材料，就不能使学生在经验与数学本质之间进行有效沟通，学生就难以真正理解背后的数学知识，反而会让数学教学陷入广而不深的形式主义泥潭。为此，教师需要精选与课程内容相匹配的素材，从整体出发分析、解读素材，展现数学知识本质，并有机融入数学学科教育教学。教师若把数学文化作为外壳，本质上仍然是传统的数学教育理念，将难以培养学生深层的数学思维。教师若仅将祖暅原理作为了解性阅读材料，学生则难以体会到这是中国古代数学家经过长期探索得到的宝贵知识财富。因此，笔者从刘徽的“牟合方盖”出发，让学生体验中国古代数学家艰难探索的过程。

（三）鼓励归纳推理，培养创造性思维

将中华优秀传统文化融入高中数学课堂，还应多引导学生发散联想，促使学生形成直觉，改变中国传统数学的刻板形象。教师可以鼓励学生从自身已有经验出发，进行归纳推理。归纳推理分为归纳方法和类比方法，归纳更多地依赖于规律的发现，类比则更多地依赖于跳跃的联想，但都是从已有经验去推理未曾经历过的东西，这与我国传统重视知识授受的教学不同，可以让学生體验数学知识发生发展的过程，从而培养学生的创造性思维。

在求解椭球体体积的过程中，类比球体体积公式求解椭球体体积公式，能够启发学生思考如何在知识之间建立联系，把握数学知识本质，从而培养学生的创造性思维。

参考文献：

［1］张维忠，李雯.中华优秀传统文化融入数学课程与教学：《义务教育数学课程标准（2022年版）》的新变化［J］.中小学课堂教学研究，2022（10）.

［2］华婧.“探究与发现”的内涵和价值：以“祖暅原理与柱体、椎体的体积”教学设计为例［J］.中学数学教学参考，2021（25）.

［3］李玟洁，陈算荣，徐倪明.融入数学史的高中数学教学研究：“祖暅原理与几何体体积”的重构设计［J］.高中数学教与学，2023（1）.

［4］汪晓勤.中华优秀传统数学文化融入高中数学教学的若干路径［J］.教育研究与评论（中学教育教学），2022（9）.

［5］岳增成，陈梓欣，林永伟.中华优秀传统数学文化进课堂：价值、标准与路径：以“出入相补原理”为例［J］.小学教学（数学版），2022（4）.

［6］郭华佳，童莉.中华优秀传统数学文化融入初中数学教科书的内容分析［J］.数学教学通讯，2023（5）.

［7］胡晋宾，刘洪璐.数学眼光的理论审视与培养建议［J］.教育研究与评论（综合版），2022（6）.

［8］姜浩哲. 我国传统数学文化融入教科书的价值、现状与展望：以人教版小学数学教科书为例［J］.课程·教材·教法，2021（1）.