转化思想在初中数学解题中的应用技巧

2023-10-26周洁

数学学习与研究 2023年11期

周洁

【摘要】现阶段，部分学生在参与初中数学解题训练的过程中耗费时间较长，极易被复杂的题目线索困扰影响解题思路，究其原因是学生缺乏转化思想.为提升学生的解题质量，文章从转化思想在初中数学解题中的应用价值出发，探究如何通过类比转化、分解转化、语言转化、等价转化、数形转化等技巧的渗透，帮助学生熟练掌握新知，提高自身的解题能力.

【关键词】转化思想；初中数学；解题技巧

转化思想是数学解题的灵魂，良好的转化思想可以帮助学生在解决问题的过程中掌握由繁化简、由难化易的基本方法，切实提升问题解决的质量.因此，教师应充分关注转化思想培育的重要价值，根据初中数学解题教学的具体要求以及学生的思维能力进行设计，帮助学生通过解题训练了解数学思想，掌握解题技巧，切实提高自身问题分析及解决问题的能力，为学生后续参与深度学习奠定基础.

一、转化思想在初中数学解题中的应用价值

由数学题目不难发现，数学解题的本质就是转化，将复杂难以解决的问题转化为便于理解通俗易懂的问题、将抽象的问题转化为直观具体的问题、将未知条件转化为已知条件等.在初中数学解题教学中，教师注重对学生转化思想的培育，具有以下价值：第一，现阶段大部分学生在遇到复杂问题、难以理解的问题时常会产生抵触心理，缺乏转化意识与转化思想，难以建立题目与所学知识之间的联系，导致在解题过程中漏洞百出，难以提高解题效率.而教师关注对学生转化思想的培育，可以使其掌握转化技巧，通过数学知识之间的内部联系完成转化，既解决学生心中的困惑，又能有效降低题目难度，提升学生的解题质量.第二，转化的目的是帮助学生掌握解决问题的基本方法，在高品质的数学课堂中，教师可以借助转化思想，引导学生掌握数、式、形相互转化的技巧，避免其在解题中出现生搬硬套公式的现象，有效提高学生解题的成功率，帮助其获得积极的情感体验.第三，在初中数学解题教学中，培养学生转化思想，可以帮助其通过训练提高自身归纳总结与空间想象能力，使学生在不断探究中达成深度学习目标，发展自身思维能力.

由此可见，利用初中数学解题教学落实转化思想的培育，能在提升解题教学质量的基础上，发展学生的思维能力，提高其核心素养.因此，教师应深入解读转化思想的具体内涵，并结合初中生的思维特点进行设计，确保全体学生都能通过训练与学习掌握转化思想在解题中的使用技巧，提升自身解题水平.

二、转化思想在初中数学解题中的应用技巧

（一）类比转化在解题中的应用

在汉语词典中，“类比”意为“就共同点对两个本质上不同的事物进行比较，并通过比喻手法的综合运用，帮助说明道理或描述某种复杂情况”.在初中数学解题中，教师可以运用类比转化技巧，指导学生寻找题目中关键线索同与之相似的数学知识的相同或不同之处，以转化的思想思考问题，降低题目难度，轻松完成问题的解答.

在解题教学中应用类比转化的技巧解决数学问题，能帮助学生由浅入深地揭示数学现象的本质，由局部到整体，梳理数学知识之间的内在联系，在提高解题质量、效率的基础上，帮助学生形成转化思想，经历从特殊到一般的解题过程，提高思维能力.

（二）分解转化在解题中的应用

“分解”即为将整体分成部分.在初中数学中，分解转化是较常规的转化思想，教师可以根据题目中的线索将复杂问题拆分为若干个小问题，引导学生循序渐进、有针对性地解决小问题，从而有效提升问题的解决质量.分解转化技巧通常可以用于较困难的综合性题目或几何问题，能有效降低题目难度.

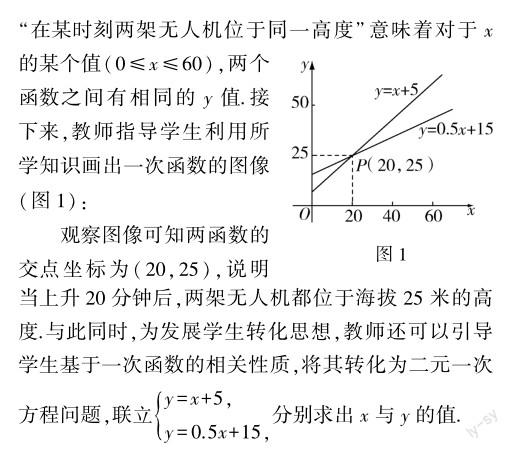
教師引导学生运用分解转化的技巧解决问题，能帮助学生缩短解题时间，快速且准确地找出问题重点，并将之转化为易于解答的问题，从而提升解题质量，促进学生转化思想的形成.

（三）语言转化在解题中的应用

数学为人们提供了一种描述与交流现实世界的表达方式.帮助学生掌握用数学语言描述现实世界的方法是初中数学核心素养中的重要内容.在解题教学中，教师应根据题目中所蕴含的数学知识，将学生难以理解的内容转化为数学语言，帮助学生以直观的方式了解题目信息，提高其解题效率.

例如，在教学“锐角三角函数”时，教师可以结合教材内提供的经典例题进行变形，为大家呈现这样一道题目：如图2，某地区为吸引游客新建一座滑雪场，施工人员打算从位于山脚下的休息室沿着山坡铺设上升魔毯，经过测量已知斜坡的坡角A为30°，为使得上升魔毯的高度为35米，需要铺设多少米的魔毯.

在初中数学解题教学中通过语言转化的方式，可以帮助学生运用数学语言建构普适的数学模型，进一步提高自身问题解决能力.与此同时，考虑到初中生的思维能力以及理解水平，在运用语言转化的过程中，教师要尽量选择与学生生活实际相贴切的表达方式，避免学生出现理解困难，影响解题的现象.

（四）等价转化在解题中的应用

解题是从未知向已知的化归转化过程，“转化”即为化归，是指在解题过程中通过变换使问题转化进而达到解决的一种方法.在初中数学中，函数与方程、未知数与已知数、空间与平面都能够进行转化，采用等价转化的方式能帮助学生将原有问题转化为新的便于解决的问题，并通过新问题的求解达到解决原问题的目的，从而提升解题质量.

例如，在教学“相似三角形”时，为帮助学生掌握等价转化技巧的具体应用，教师可以为学生提供这样的一道题目：如图3，在△ABC中，AB=7，AC=11，M是BC的中点，MF∥AD交AC于F，且AD平分∠BAC，求FC的长度.

在解题教学中，教师可以指导学生根据已知线索出发，设∠BAD为∠1，∠DAC为∠2.此题目求FC的长度，但是从图中难以看出FC与哪条线段相等，因此，根据已知线索“M是BC的中点”，可以设AC中点为N（图4）：

教师将等价转化思想渗透于解题教学中，能帮助学生以直观的方式在短时间内理解题意，从而帮助学生在总结数学方法的过程中提高自身的学习能力，为后续参与深度探究奠定基础.

（五）数形转化在解题中的应用

数形转化是初中数学解题中较常见的一种转化方式，教师帮助学生掌握数形转化的解题技巧，可以使其掌握数形结合的思想方法，经历解题过程，感悟数形结合的意义，在提高解题效率的基础上，发展自身推理能力与运算能力，这对提高学生核心素养具有积极作用.

例如，在教学“函数”时，在本单元学习中，教师可以为大家提供这样一道题目：求|x+1008|+|x-1007|的最小值，按照传统方法，解决此题目前需要运用零点分段法进行分类讨论，但解题过程较复杂，学生在计算中容易出现失误.基于数形结合转化思想，教师可以指导学生回顾绝对值的几何意义，得到|a-b|表示数轴上a，b两点之间的距离，因此将原式可变化为|x-（-1008）|+|x-1007|，并利用数轴表示其几何意义（图5）：