双定子同极内嵌永磁游标电机转子永磁体极弧系数优化
2023-10-25张进
张 进
(广安职业技术学院,广安 638000)
0 引 言
永磁游标电机由磁齿轮演化而来,满足磁场调制原理,能够实现低速大转矩输出,其传动比定义为转子极对数与定子绕组极对数之比[1]。近年来,研究者在电动汽车[2]、机器人[3]和风力发电[4]等领域对永磁游标电机开展了深入研究,提出了同轴式[2-4]、轴向式[5]和直线式[6]等结构类型。文献[7]对永磁游标电机进行了综述,指出永磁游标电机三个主要研究方向,包括提高转矩、提升功率因数和降低成本。
双定子结构能够有效改善永磁游标电机的功率因数[8-9],同时由于集成度高,其转矩密度大。双定子电机的两个定子共用一个转子,双定子分别控制能够实现多种运行模式[10]。研究者通过设计和优化共用转子结构,进一步提升电机的性能。目前,转子结构主要包括:(1)传统表贴式,即S极和N极永磁体交替黏贴于转子轭表面[11];(2)轮辐式,即具有聚磁效应的S极和N极镶嵌于铁心极之间且磁极沿周向充磁[12];(3)V形式,S极和N极永磁体以V字形内嵌于转子铁心中[13];(4)同极内嵌式,即充磁方向相同永磁体嵌于转子内外两侧表面[8]。其中,同极内嵌式永磁转子与传统表贴式永磁转子相比,永磁体用量明显减小,与轮辐式和V形式永磁转子相比,工艺相对简单,同时由于有转子轭支撑,结构可靠性高。
双定子同极内嵌永磁游标电机(以下简称DS-CP-PMVM)可以看作半数的充磁方向相同的永磁极被铁心极取代。然而,当永磁体用量减少一半时,转子转矩明显降低[14]。本文从减少永磁体用量、提高输出转矩出发,对DS-CP-PMVM的转子进行优化设计,重点分析转子永磁体和定子的最优位置,优化永磁体极弧系数,并对优化后的双定子游标电机的电磁性能进行讨论。
1 电机结构
之前的工作中,我们制备了一种DS-CP-PMVM,样机如图1所示,对应的拓扑结构如图2所示。实质上DS-CP-PMVM由两个游标电机组成,内外电机采用相同配置,定子为分裂齿结构,主槽数为9,定子绕组为集中绕组形式,与文献[8]中开口槽定子相比,集中绕组端部短,铜耗少,且工艺相对简单;内外电机共用一个转子,转子为双侧同极内嵌结构,单侧永磁体充磁方向一致,且沿圆周均匀分布。

图1 DS-CP-PMVM样机
由于内外侧配置相同,绕组极对数pe-x=pe、转子极对数pr-x=pr、定子分裂齿个数Nst满足磁场调制条件:
Nst=pe+pr
转子永磁体的尺寸有厚度和弧长,其中,弧长与极弧系数有关。极弧系数可定义[14]:
式中:下标x代表内侧或外侧,x=i代表内侧,x=o代表外侧;βx和τx分别表示永磁体的弧长和极距。转子内外侧永磁体中心轴线之间的夹角为αd-d。
DS-CP-PMVM采用三相交变电流驱动,三相电流输入:
式中:Iamp-x为相电流幅值;f为交流频率。图2中,内外定子A相轴线的夹角表示为αA-A。定子绕组通以交变电流产生的同步速度ne=60f/pe与转子转速nr之比:
图1样机的参数如表1所示,样机转子永磁体采用矩形结构。转子转速为200 r/min时,测得样机的反电动势如图3所示,内外定子反电动势波形近似正弦。
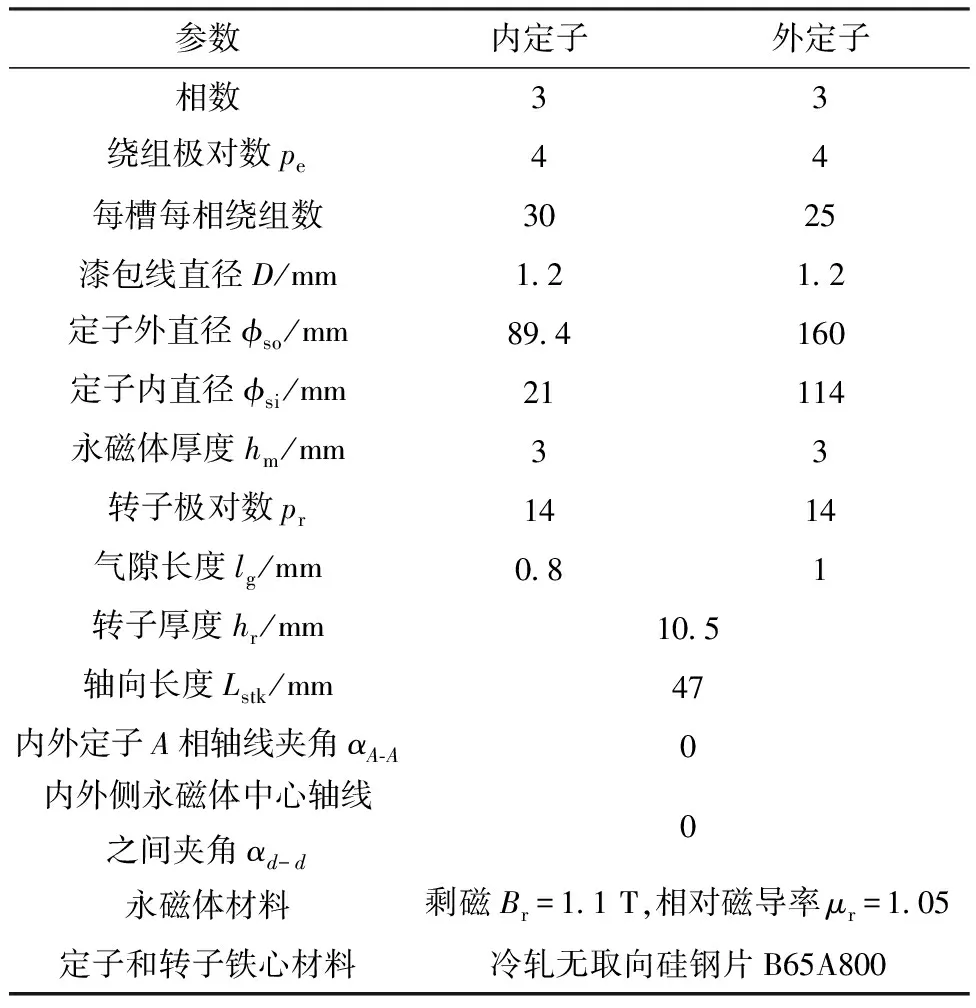
表1 DS-CP-PMVM结构参数
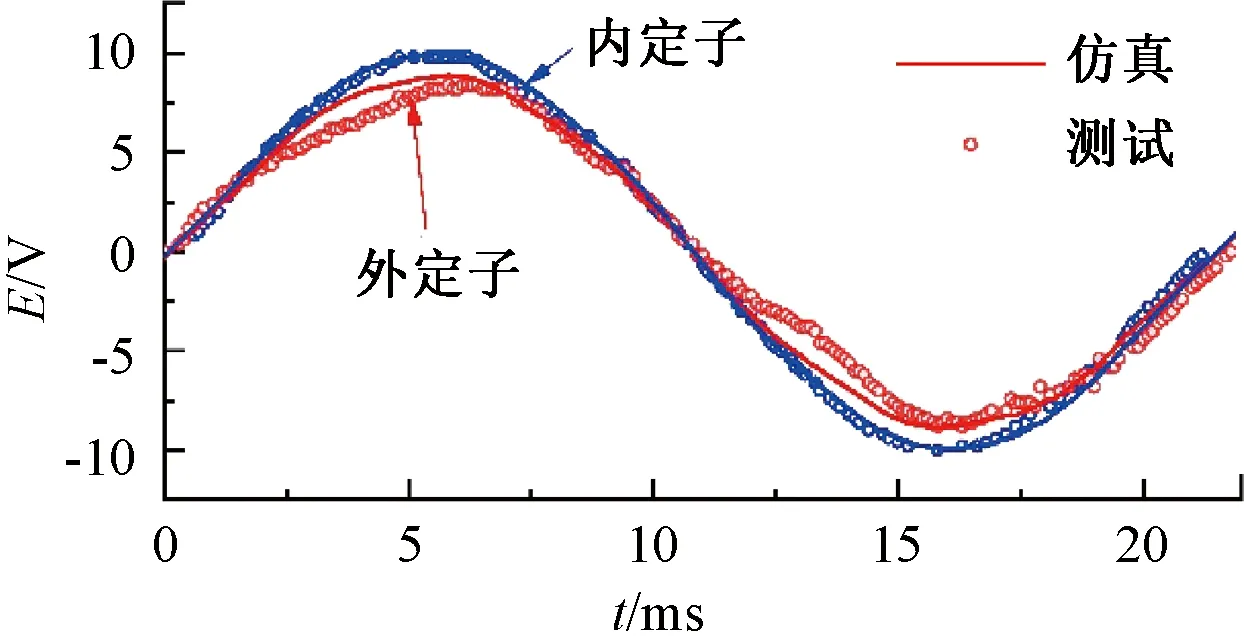
图3 DS-CP-PMVM样机反电动势
2 转子优化
2.1 参数αA-A和αd-d优化
相对角度αA-A和αd-d对电机的性能影响很大,图4为不同αA-A,αd-d下,DS-CP-PMVM的磁力线分布。αA-A=0,αd-d=0和αA-A=7°,αd-d=7°时,主磁力线直接连接内外定子,表现为磁场耦合;αA-A=0,αd-d=180°/pr=12.86°时,内外定子的磁路处于解耦状态;当αA-A=180°/Nst=10°,αd-d=180°/pr=12.86°时,内外定子的磁路部分解耦、部分耦合。
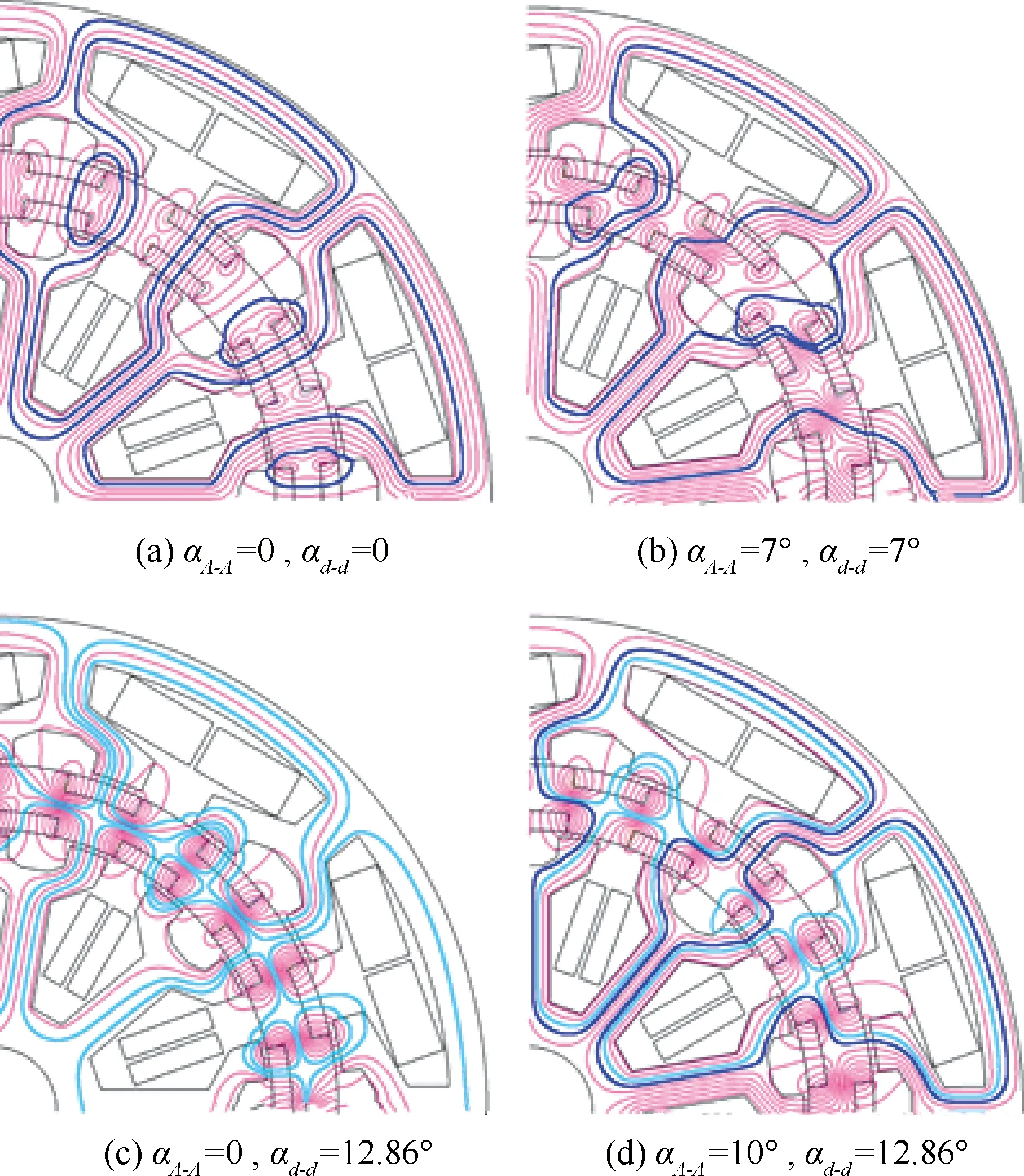
图4 DS-CP-PMVM磁力线分布
取转子内外侧永磁体极弧系数Kpm-i=Kpm-o=0.5。当内外定子电流Iamp-i=Iamp-o=6 A时,DS-CP-PMVM输出转矩随αA-A,αd-d的变化图谱如图5所示。当αA-A=αd-d时可获得最大转矩输出,为设计方便,优选αA-A=0,αd-d=0。
2.2 转子永磁体极弧系数优化
图6对比了DS-CP-PMVM(Kpm-i=Kpm-o=0.5)与相同尺寸双定子表贴式永磁游标电机(以下简称DS-SM-PMVM)的输出转矩,转子永磁体用量减少一半,相应的输出转矩会降低,内外定子电流均为6 A时,DS-SM-PMVM的平均转矩为7.49 N·m,而DS-CP-PMVM的平均转矩为6.89 N·m。针对单定子永磁游标电机,文献[14]通过优化转子永磁体极弧系数,在一定定子电流范围内,有效提高了输出转矩。这里,将转子永磁体极弧系数优化拓展到DS-CP-PMVM。
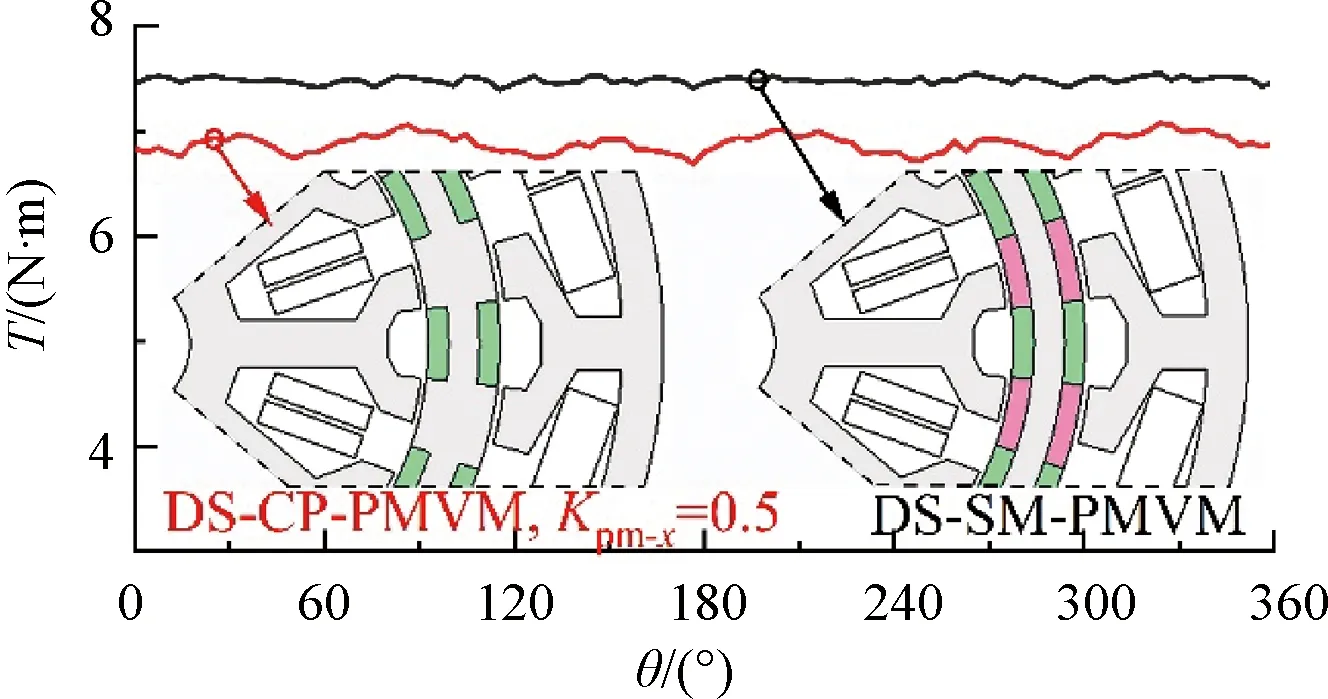
图6 Iamp-i=Iamp-o=6 A时,DS-CP-PMVM(Kpm-i=Kpm-o=0.5)与DS-SM-PMVM转矩对比
DS-CP-PMVM的输出转矩Te可表示为Kpm-i和Kpm-o的函数,即:
Te=f(Kpm-i,Kpm-o)
转子两侧永磁体极弧系数的优化公式:
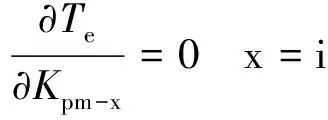
Iamp-x=6 A时,DS-CP-PMVM输出转矩Te与Kpm-x关系云图如图7所示。当Kpm-i=0.62,Kpm-o=0.66时,Te近似最大值。此外,图7最内层等转矩线包含的区域内,输出转矩比较接近,最大偏差小于0.15 N·m。
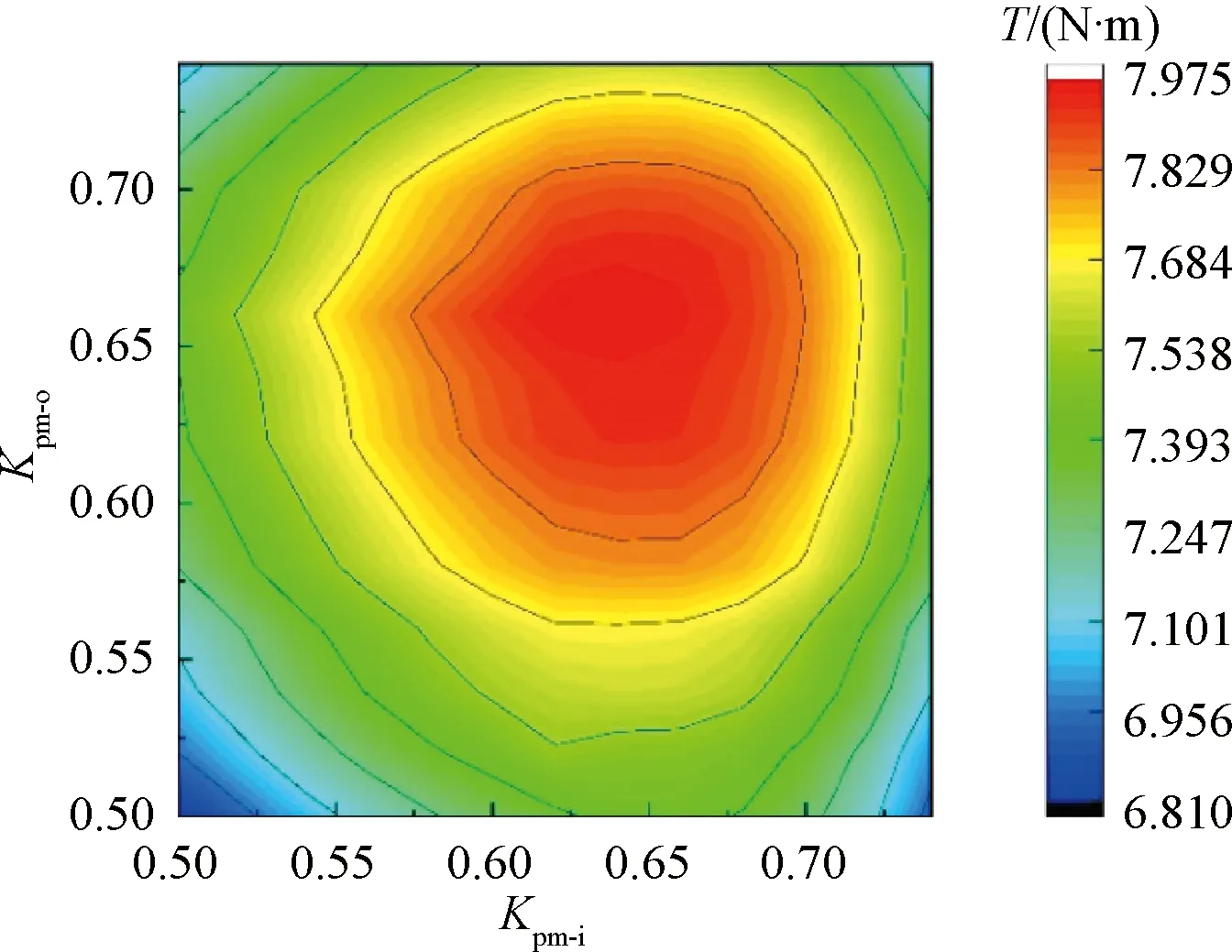
图7 Iamp-x=6 A时,DS-CP-PMVM转矩与Kpm-x关系云图
3 优化后DS-CP-PMVM的电磁性能
取Kpm-i=0.62,Kpm-o=0.66,DS-CP-PMVM反电动势幅值与转子转速的关系如图8所示。反电动势幅值随转子转速的增大而增大,且呈线性关系。图1样机的转子极弧系数约为Kpm-i=0.64,Kpm-o=0.6,对应图3反电动势幅值与优化后电机相同转速下的反电动势近似。
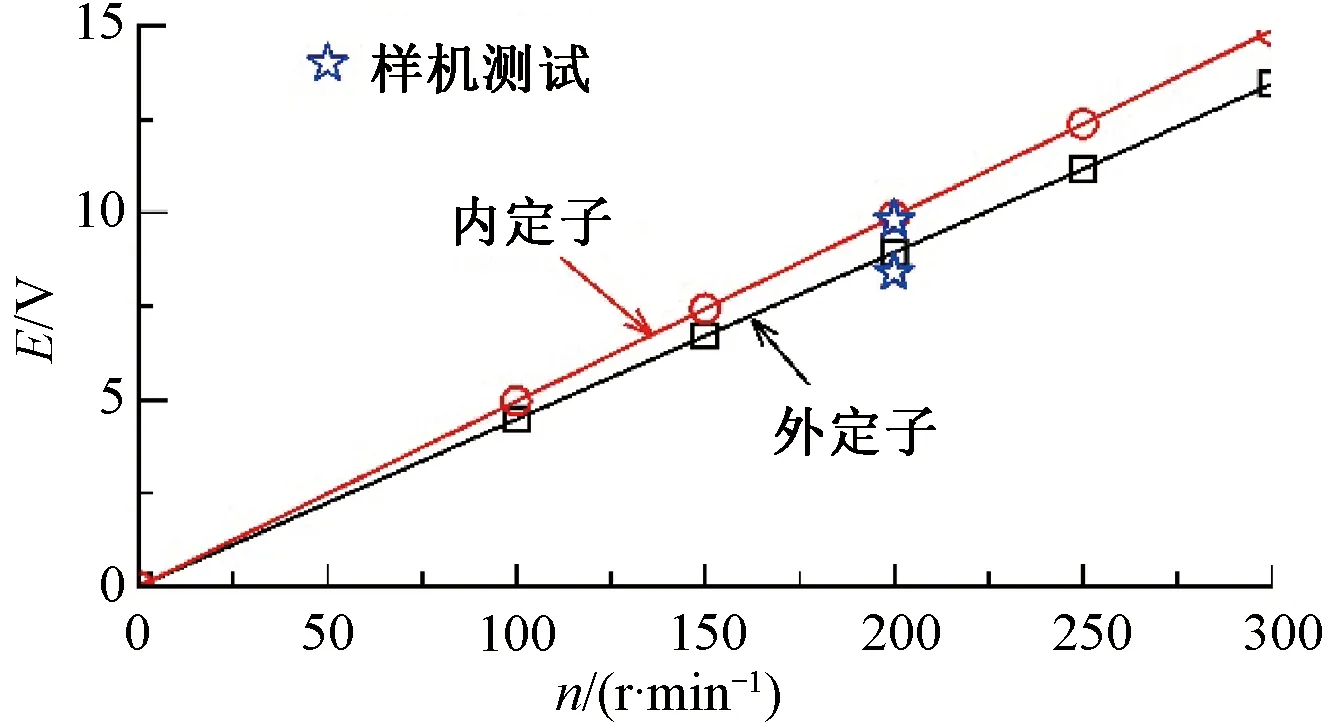
图8 优化后的DS-CP-PMVM反电动势幅值与转子转速的关系曲线
优化后的DS-CP-PMVM转子转矩与Iamp-x关系云图如图9所示。对于单侧定子而言,转子转矩随定子电流的增大而增大;转子转矩是内外定子共同作用的结果,如图2(b)所示,转子转矩为转子内外侧转矩之和,即TL=Te-o+Te-i。如图10所示,当Iamp-i=Iamp-o=6 A时,转子转矩为(7.97±0.16)N·m,比图6的DS-SM-PMVM转子转矩提升了(7.97-7.49)/7.49=6.4%,能够满足永磁体用量减少而转矩能力不降低。
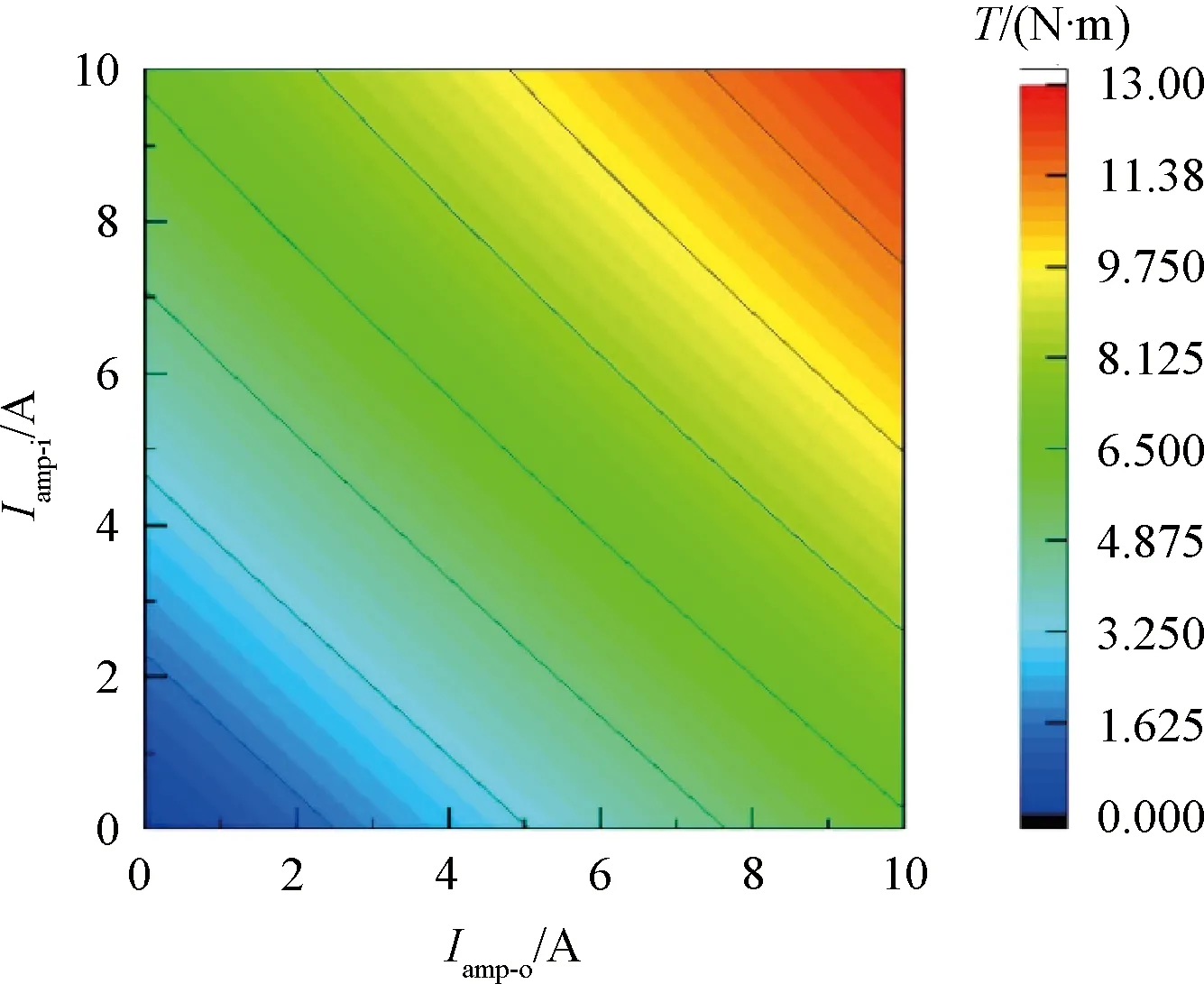
图9 优化后的DS-CP-PMVM转子转矩与Iamp-x关系云图
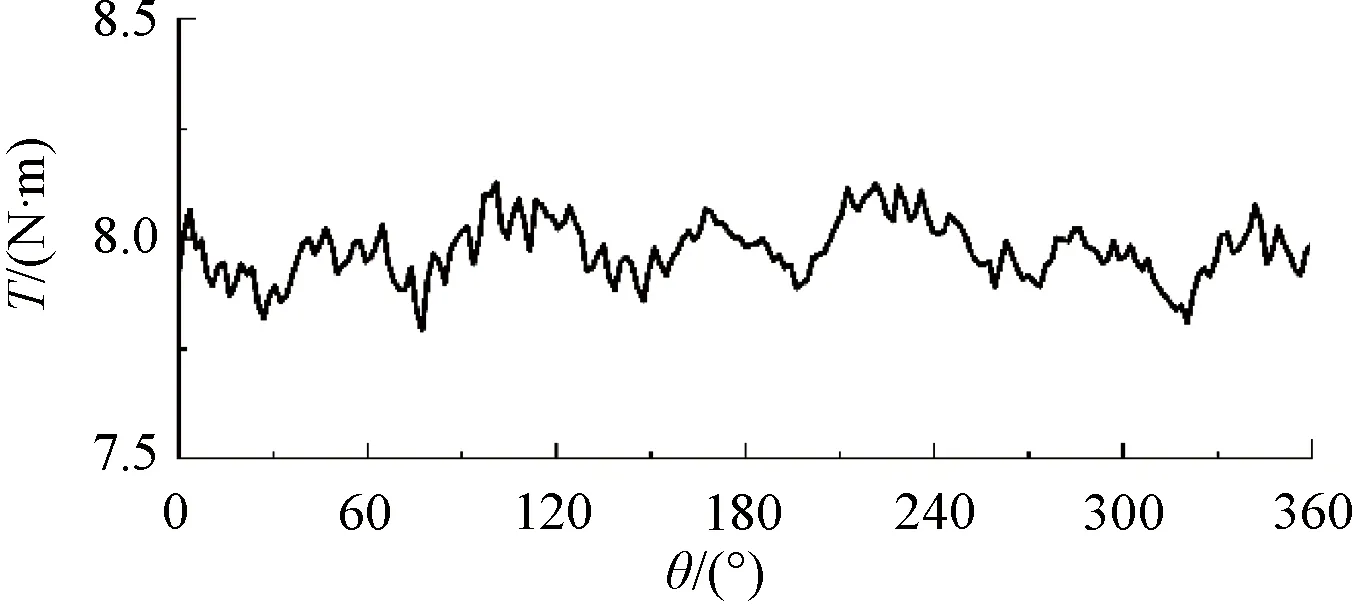
图10 Iamp-x=6 A时,优化后的DS-CP-PMVM转子转矩
4 结 语
本文针对DS-CP-PMVM,以预先制备的样机为基础,讨论了DS-CP-PMVM的结构与工作原理,并对同极内嵌转子永磁体极弧系数进行了优化研究。
分析了DS-CP-PMVM磁力线分布,当转子内外侧永磁体中心轴线夹角αd-d与内外定子A相轴线夹角αA-A相同时,主磁力线直接连接内外定子,电机表现为磁场耦合,且输出转矩最优,本文取αA-A=αd-d=0。
讨论了转子永磁体极弧系数对DS-CP-PMVM转矩的影响,当转子内外侧永磁体极弧系数分别为Kpm-i=0.62,Kpm-o=0.66时,DS-CP-PMVM输出转矩最大。
讨论了DS-CP-PMVM的电磁特性,在Iamp-i=Iamp-o=6 A时,当Kpm-i=Kpm-o=0.5,转子转矩比传统DS-SM-PMVM低,而优化后的DS-CP-PMVM,转矩提升了6.4%。
