燃料电池空压机用永磁电机降振优化设计

王德猛,尹红彬,张 军,于新龙,张学义

(1.山东理工大学 交通与车辆工程学院,淄博 255049; 2.山东唐骏欧铃汽车制造有限公司,淄博 255049)

0 引 言

作为燃料电池空压机内的核心部件,高速电机受到广泛的关注。空压机用电机主要有两种类型,一种是电励磁电机,另一种是永磁电机。较传统的电励磁电机而言,永磁电机内部器件数量减少,从而增加了内部的空间利用率,且其无励磁电阻损耗,效率更高,运行更加稳定[1]。随着新材料的开发与应用,与新材料紧密相关的永磁电机也广泛应用到新兴领域中,得到了进一步的发展。在保证其高功率密度和宽调速范围的同时,要降低电机的振动噪声,燃料电池空压机用永磁电机的振动噪声优化问题成为了近年来工程领域研究的热点。

电机振动有多种类别,如电磁振动、机械振动、空气动力学振动等[2],其中,电磁振动所占比例较大[3]。电磁噪声由电源控制单元的PWM谐波引起,或者是由电机的过度电磁谐波引起[4]。空气噪声是由风扇、转子和气流效应产生的,气流效应是由沿风向移动时的气流产生的。当电机转速较高时,空气噪声起主导作用[5]。机械噪声主要是由移动的转子、轴承、电机的电刷、滑环或换向器摩擦引起的。实验表明,电机噪声中,气动噪声占57.5%,转子和轴承引起的机械噪声占27.7%,电磁噪声占14.8%[6]。研究发现,电磁噪声的强度主要由负载决定,而机械噪声和空气动力噪声则取决于电机的速度[7]。

近年来,许多研究学者对永磁同步电机(以下简称PMSM)、开关磁阻电机、感应电动机、混合励磁电机的振动和噪声进行了研究。振动和噪声的研究涉及电磁、结构、力学、声场等多个方面。通过电磁力和模态分析,阐述了PMSM中振动和噪声的运行机理[8]。

文献[9]运用有限元仿真,对于电机的0阶主要电磁激振力波,通过结构参数分析了对电机空载气隙磁场的影响,且采用了调整定子槽口宽度和偏心气隙的两种方法,实现了电机振动噪声的抑制。文献[10]构建有限元模型,运用Workbench分析电机外壳的振型和固有频率,建立三种不同参数和因素的模型,综合考虑结构参数对电机进行优化。文献[11]对原始瞬态磁场进行仿真分析,对电机磁密进行谐波分析,结合多目标优化算法,建立声场模型对噪声瀑布图进行对比。文献[12]应用麦克斯韦张量和磁势乘磁导法,通过注入电流谐波,构建了描述0阶径向电磁力波的解析表达式,进一步深入探究了该现象的机理。

本文以一台功率为20 kW的车用燃料空压机用永磁电机为研究对象,首先分析这台电机的结构,并根据它的主要参数建立一个二维模型,接着对电磁特性进行分析,并提出优化方案,最后,对这台电机的性能进行评估。

1 PMSM结构

燃料电池空压机用PMSM二维截面示意图如图1所示。该电机为一台24槽4极整数槽单层短距分布绕组PMSM,其主要参数如表1所示。

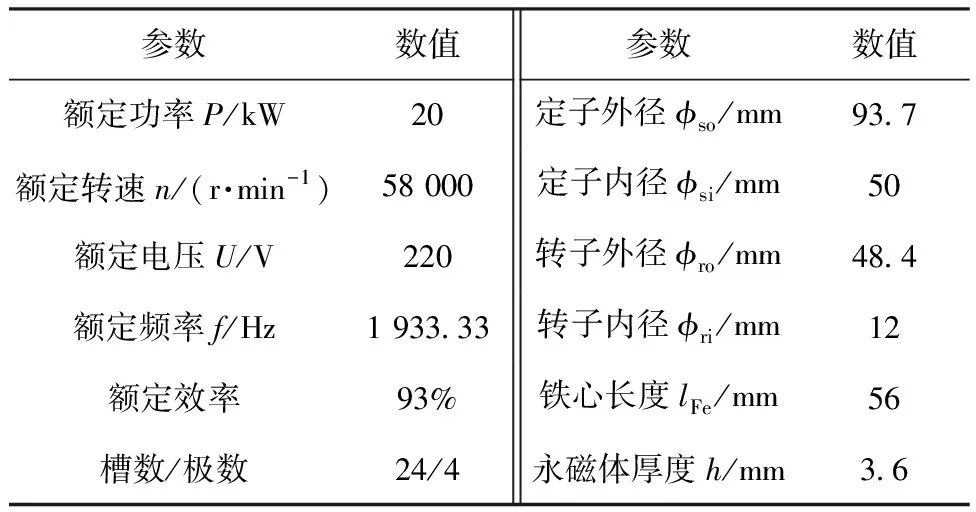
表1 PMSM主要参数

图1 PMSM二维模型

在对电机进行负载工况的磁场分析时,把转速设置为额定转速58 000 r/min。对电机的三相定子绕组添加激励源,且电机三相绕组为Y型连接。设定电机相关部件的材料属性,增加瞬态场求解器进行计算,能够看到负载工况下的性能状况,进而判断出电机设计是否合理。

2 PMSM电磁特性分析

2.1 电机磁场分析

搭建电机二维有限元解析模型,模拟电机额定工况下的运行过程。采用对称三相电压源来模拟电机的起动响应。图2(a)显示了电机的磁密分布云图,定子齿部的磁密为1.49 T,定子轭部的磁密为1.37 T。通过传热学分析,我们发现,当电机处于额定工况时,它能够满足散热需求。图2(b)为某时刻下的电机磁力线分布图,电机磁力线分布均匀。

2.2 电机径向电磁力分析

电机定子齿部承受径向电磁力的影响,这种影响可能会导致电机产生电磁振动噪声[13]。在深入探讨这种影响前,需要通过麦克斯韦张量法来精确计算径向电磁力,并将其转化成可以被实际应用的数值。我们确定定子铁心结构承受的径向电磁力的密度,并将其表示[14]:

(1)

式中:fr为电磁力径向分量;Br为气隙磁密径向分量;Bt为气隙磁密切向分量;μ0为真空磁导率,μ0=4π×10-7H/m。

在磁导率上,空气远远小于铁磁材料。当磁场穿过定转子铁心时,磁场会与其表面呈现出一种垂直的关系。在这种情况下,径向气隙磁密度远大于切向气隙磁密度,因此可以忽略切向磁密度。在结构上,定子铁心径向电磁力近似:

(2)

在电机定转子间组成的气隙处,磁通密度主要包括两种:一种是永磁磁动势产生的转子磁密BRδ,另一种是电枢反应产生的定子磁密BSδ,因此式(2)可表示[14]:

(3)

BRδ=FRλδ

(4)

BSδ=FSλδ

(5)

式中:FR为永磁体磁场产生的气隙磁动势;FS为定子电枢反应磁动势;λδ为等效气隙磁导。

FR和FS可按下式计算[15]:

(6)

(7)

把式(4)～式(7)代入式(2)中,得出定子齿部受到的径向电磁力计算表达式。用该表达式计算求解径向电磁力波的空间阶数,分别是(νR±νS)p、(νR±νS)p±Z、(νR±νS)p±2Z、频率为(νR±1)f1,其中f1为电机基波电频率[16]。

相对于阶次较高的径向电磁力所引起的较小噪声,阶次较低的电磁力所引起的噪声较大。本文根据此规律,将24槽4极电机的相关数据参数代入到式(2)中,得出空间阶次和频率倍数,如表2所示。

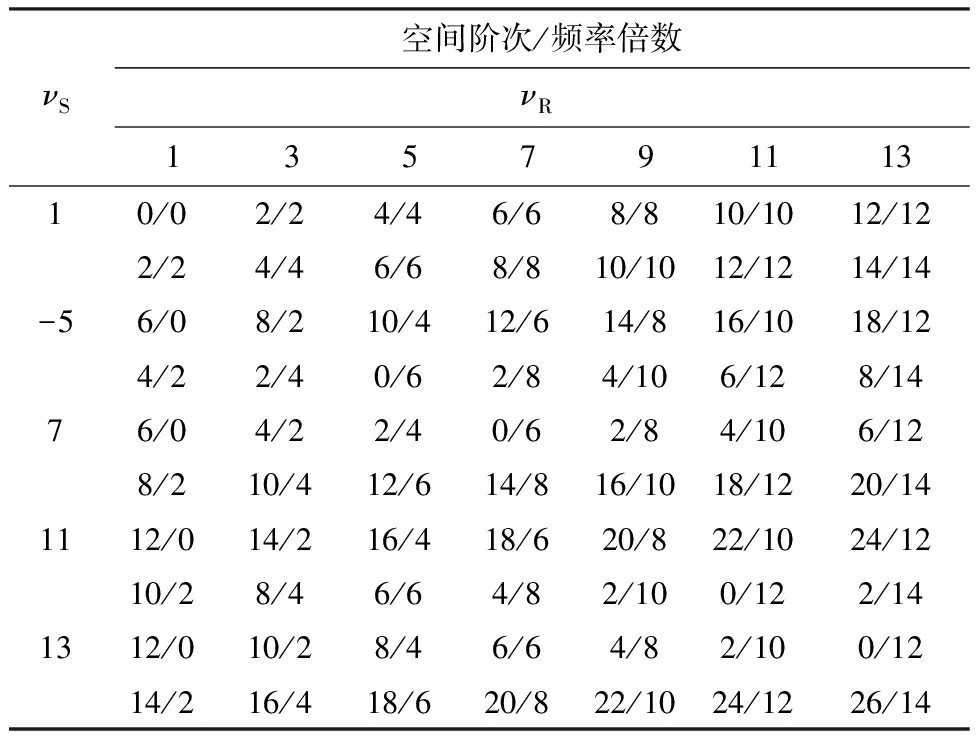
表2 PMSM径向电磁力的空间阶次与频率倍数

PMSM的电磁振动噪声往往与其电磁场有关,其中重要的就是径向电磁力。通过调整电机的磁场分配和电机的电磁磁路优化来减小振动噪声,就能够有效地抑制电机的振动和噪声。

3 电机降振优化设计方案

减小作用在电机定子齿部的径向电磁力,能够降低电机振动幅值。根据电机振动噪声出现的原理,给出基于隔磁磁桥间距d改善修型设计方法,将电机原模型中的隔磁磁桥间距增加,在优化过程中同时改变隔磁磁桥长度。

图3为在不同隔磁磁桥间距下所得到的电机径向气隙磁密幅值。由图3可知,隔磁磁桥间距d逐渐增大,径向气隙磁密幅值随之降低。其原因是偏移距离增加后的隔磁磁桥,磁路有效长度变长,磁阻提升,等效气隙磁导λδ变小,进而使得径向气隙磁密减小。

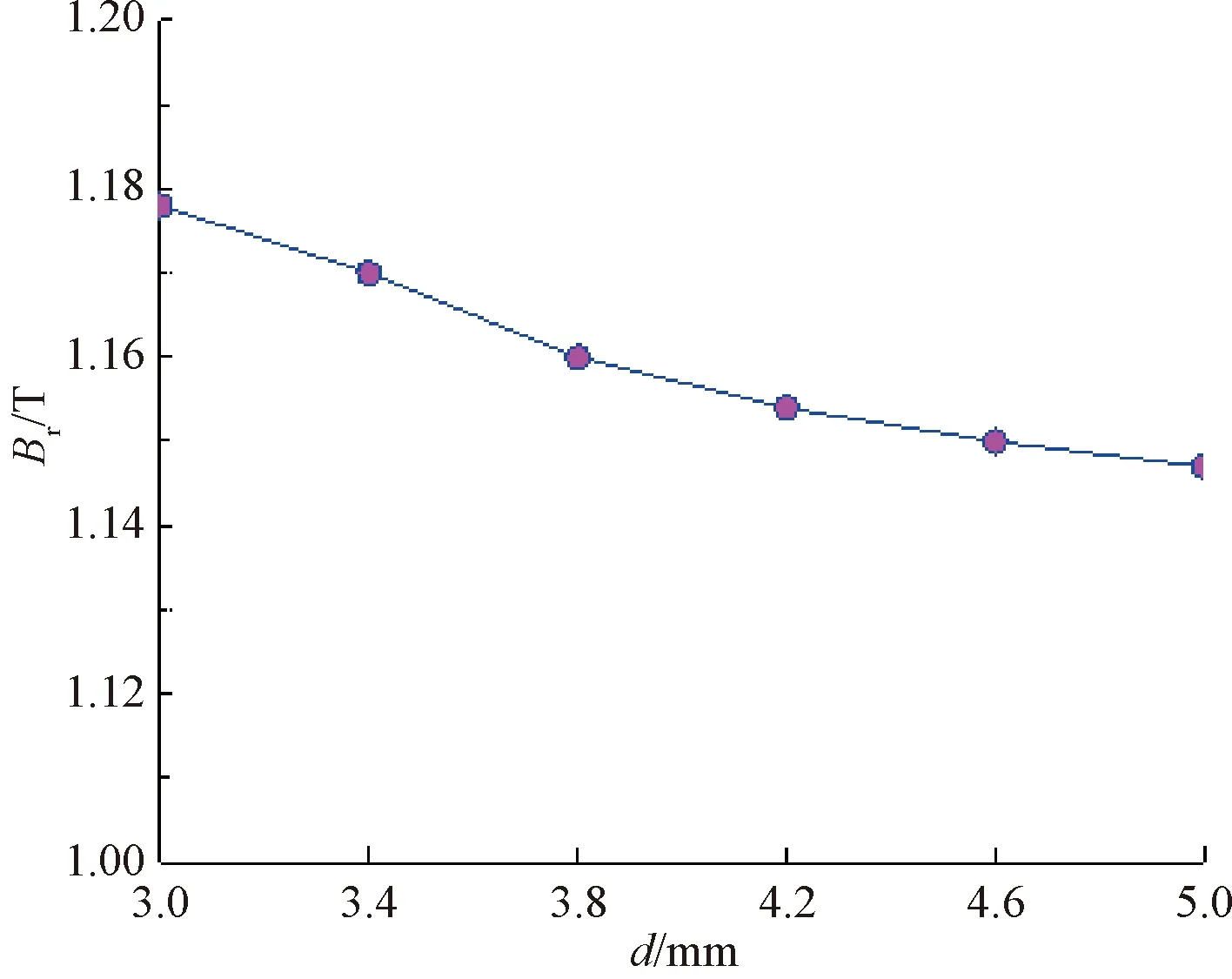
图3 隔磁磁桥间距与径向气隙磁密幅值关系

在优化转子隔磁磁桥的同时,还需要考虑电机的电磁性能。图4为隔磁磁桥间距d值与漏磁系数δ的关系图。可以看出,当偏移距离在4.6 mm之前时,电机漏磁系数上升程度较小,在4.6 mm之后,漏磁系数出现明显上升。通过观察对比,最终确定4.6 mm为隔磁磁桥间距设计值,并以图5的形式展示了经过优化的电机转子结构。

图4 隔磁磁桥间距与漏磁系数关系

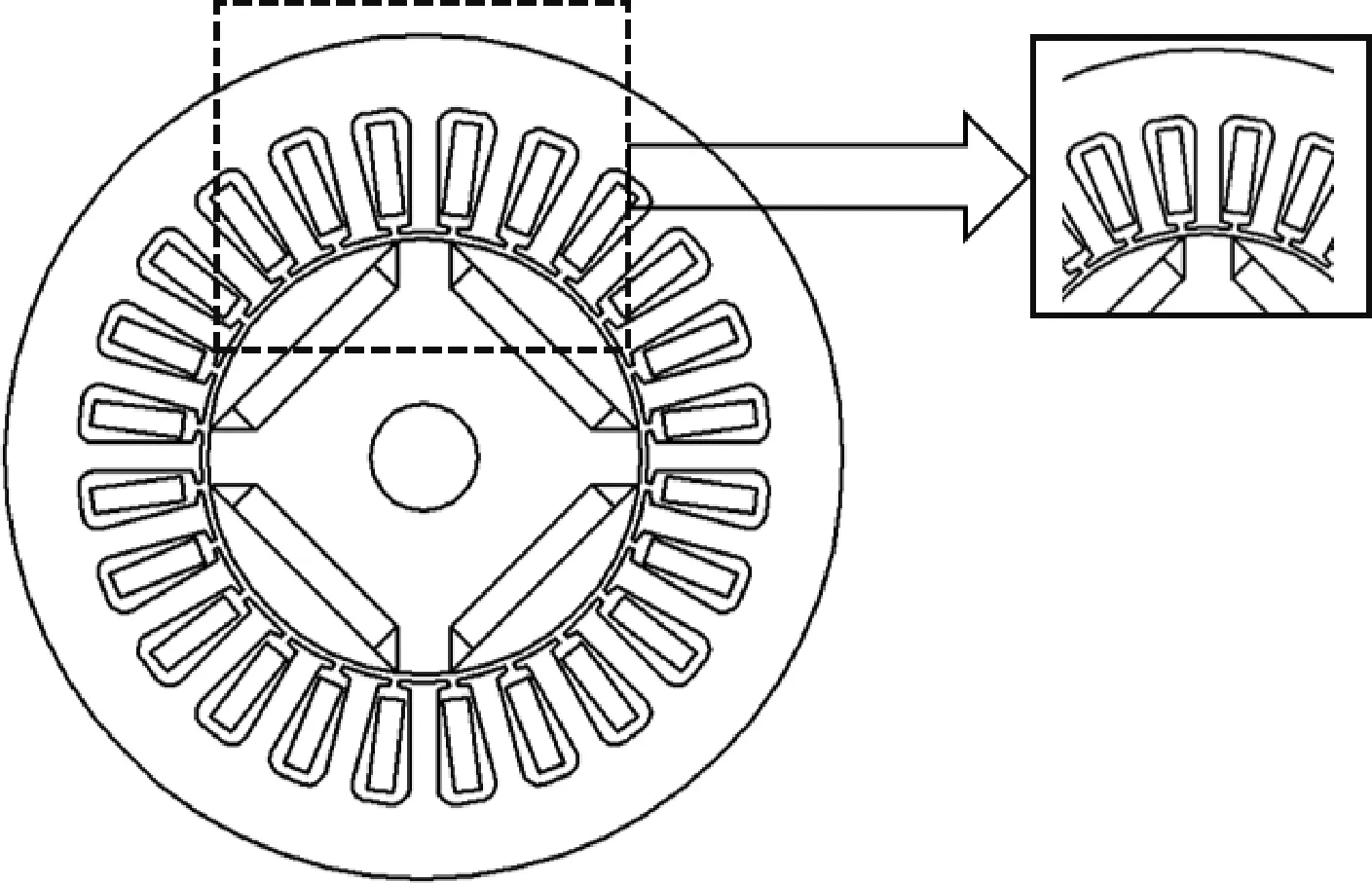
图5 电机转子优化方案

图6 电机优化前后径向电磁力波形

4 优化后电机性能计算

4.1 电机电磁计算分析

针对优化前后的电机方案分别进行电磁有限元仿真求解。取气隙中间一处作为磁场观测点,求解电机负载工况下的径向电磁力,得到的仿真结果如图 6所示。由波形图优化前后对比发现,径向电磁力密度的幅值有所下降。

图7与图8给出了电机输出转矩与齿槽转矩的波形。由图7、图8可知,优化后的输出转矩略有下降,但仍可满足电机输出性能要求。同时,优化后的电机转矩脉动与齿槽转矩性能有所改善。

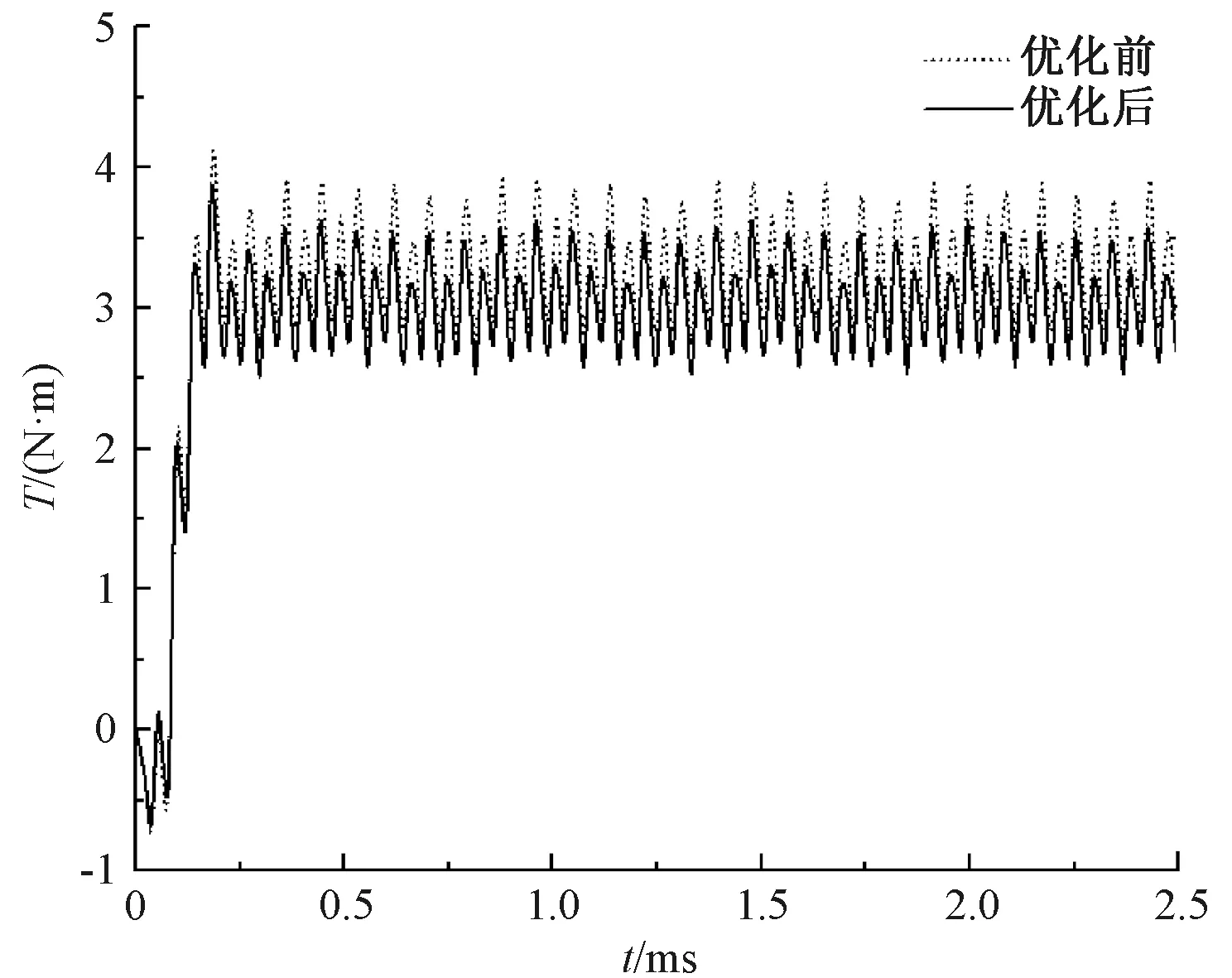
图7 电机优化前后的输出转矩波形

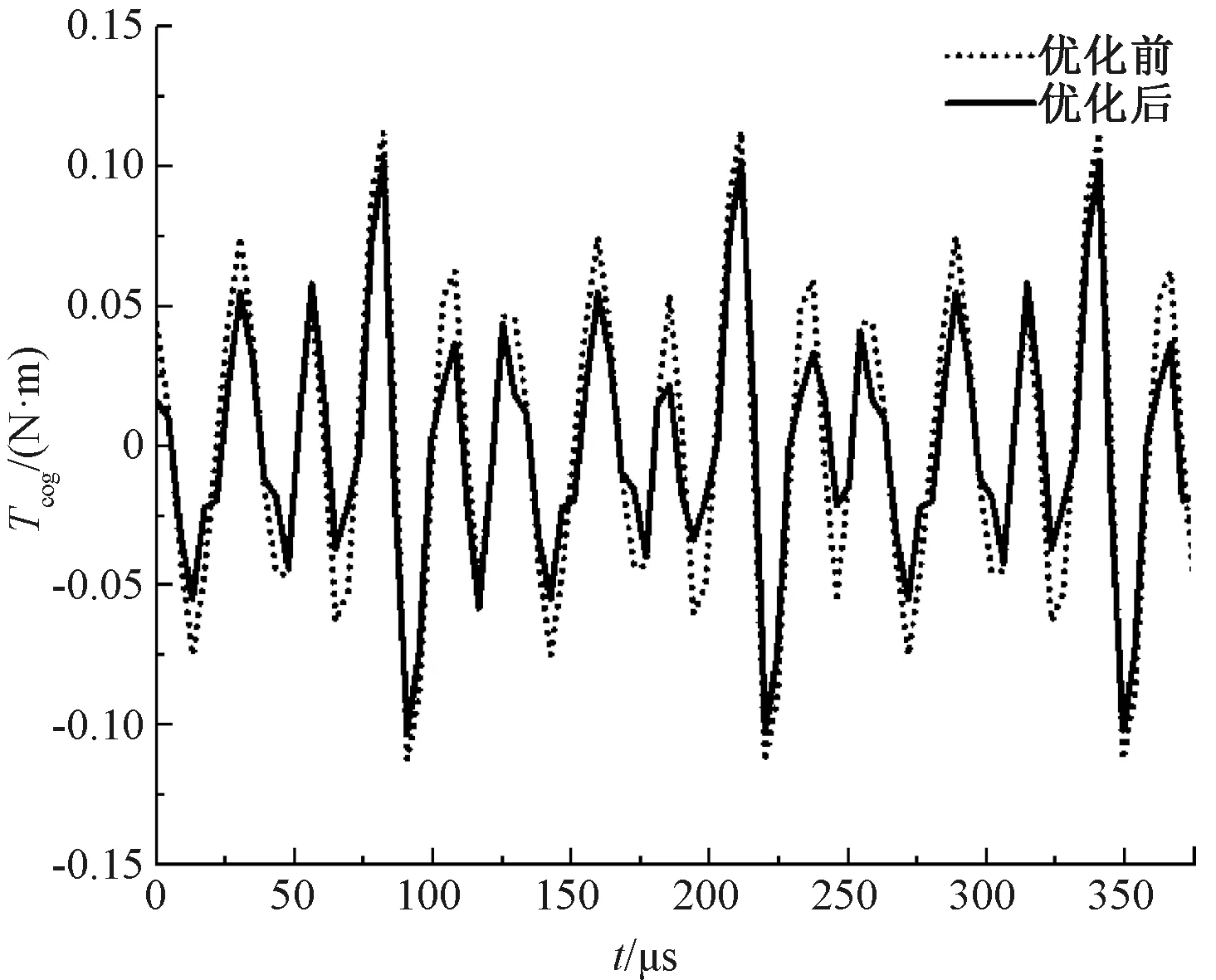
图8 电机优化前后的齿槽转矩波形

4.2 电机模态分析

在电机运转时,作用于定子齿部的外施电磁力频率与固有频率接近或相等时,将发生共振[17]。若共振时电机继续运转,就可能造成严重的损失,影响电机的正常使用和寿命。特别是对于电动汽车,出现这种情况,就可能导致严重的安全问题。采用模态分析,可以更加精确地测量出电机的固有频率,从而防止出现共振的问题。目前,解析法和有限元法是模态分析的两种主要手段,有限元法现已逐渐替代计算复杂性和不准确性的解析法[18]。本文对电机的定子模态进行求解采用的是有限元分析方法,通过计算得到的电机定子各阶模态振型及固有频率如图9所示。

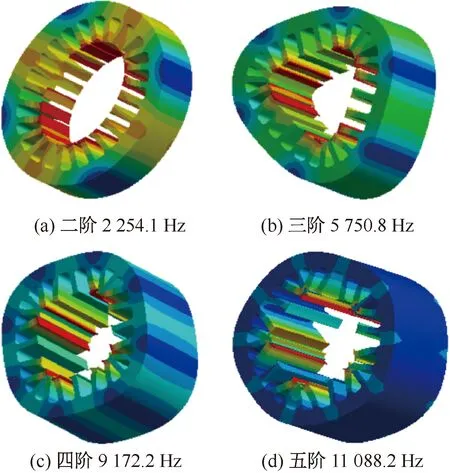
图9 电机定子模态振型图

由前面的分析可知,定子齿部所受径向电磁力主要是偶数倍基频分量。通过模态分析求解得出定子模型固有频率。对比发现,计算出的径向电磁力主要谐波频率值与定子固有频率值有较大的差距,这表明该电机不会出现共振问题,而且设计也较为合理。

4.3 电机振动分析

通过构建电机有限元振动谐响应三维模型,先将有限元瞬态场中的径向电磁力求解完成后,再传递到结构场,在定子齿部加入振动激励源,最后将电磁场与结构场耦合仿真。通过对法兰盘的螺栓孔进行约束,计算出当额定转速58 000 r/min时,电机壳体外表面上的某一监测点振动速度幅频特性曲线,如图10所示。

由图10可知,观测点的振动速度在偶数倍基频等处幅值较为明显。由表2可知,同这些频率点所对应的径向电磁力分量幅值都较高,使得振动速度幅值随之变大。振动速度幅值经优化后整体下降,偶数倍基频时下降更为明显。

通过应用隔磁磁桥修形方法,我们可以对电机结构进行优化,从而显著降低其径向气隙磁密度,还能保证电机的电磁性能,表明了该优化方法的准确性与实用性。

5 结 语

本文旨在探讨一种新型的降振优化方法,采用了一种基于隔磁磁桥修形的技术,可以有效改善功率20 kW燃料电池空压机用内置径向式PMSM的结构参数,从而减少径向电磁力,同时能够有效地降低齿槽转矩,并且保证其输出性能的合理性,从而达到良好的降振效果,为车用PMSM的优化设计、振动噪声的降低提供了工程参考。