PMLSM伺服系统自适应非奇异快速终端滑模控制
2023-10-25赵希梅
张 猛,赵希梅
(沈阳工业大学 电气工程学院,沈阳 110870)
0 引 言
采用永磁直线同步电动机(以下简称PMLSM)的直线驱动控制系统在结构上省略了滚珠丝杠等设备,零部件大大减少,且PMLSM拥有速度快、精度高、体积小、安全可靠性高等优势[1],因此,PMLSM在高速高精度生产制造方面十分常见[2]。但是,在生产制造中PMLSM伺服系统会受外部扰动等不确定性影响,所以选取合适的控制策略是十分必要的[3]。目前,简单的控制策略很难满足工业生产的需求,复合控制策略更加受人们的青睐,因此未来研究方向更加趋向于复合控制策略。
滑模控制(以下简称SMC)具备强鲁棒性、模型简单、响应速度快等优势,在轨道交通、机械臂、智能控制等领域得到广泛应用[4-6]。但是,SMC的强鲁棒性会带来一个显著缺点即抖振现象,抖振大大影响了整个系统的控制性能[7-8]。
文献[9]设计的终端滑模面明显提高了快速性,同时利用神经网络来补偿系统的不确定性,但终端滑模面所带来的奇异问题仍无法避免。文献[10]采用复合控制策略,结合自适应与SMC,对控制器中的未知参数进行估计,抖振现象减弱明显,但快速性仍未有明显改善。文献[11]采用的滑模面是积分类型的,不同于常用的滑模面,不会受到滑模面中微分项的影响,但同时切换函数所带来的抖振问题仍然存在。
本文设计了自适应非奇异快速终端滑模控制(以下简称ANFTSMC)方法,能够有效提高系统的收敛速度,解决了收敛速度慢的问题,并保证位置跟踪精度,避免奇异性。同时,自适应律的加入能够实时估计系统未知扰动的上界,系统的鲁棒性有所提高。最终,仿真对比分析表明,同SMC和NFTSMC方法对比,本方法能够在保证快速收敛性和跟踪精度的情况下,具有较强的鲁棒性能。
1 PMLSM数学模型
系统采用表贴式PMLSM,建立相应的数学模型,来实现PMLSM的矢量控制。PMLSM在两相旋转坐标系中的电压方程如下:
(1)
磁链方程:
(2)
式中:ud,uq为d,q轴的电压;Rs为定子电阻;id,iq为d,q轴电流;ψd,ψq为d,q轴磁链;Ld,Lq为d,q轴电感;v为动子速度;ψf为永磁体励磁磁链;p为极对数;τ为极距。
电磁推力Fe方程:
(3)
(4)
(5)
式中:Kf为电磁推力系数。
PMLSM的机械运动方程:
(6)
式中:M代表动子总质量;B代表粘滞摩擦系数;FL代表系统外部集总扰动,包括但不限于摩擦力、负载扰动和端部效应力。
忽略扰动FL的影响,可获得理想状态下的动态方程:
(7)
式中:d为动子位置信号;定义An=-B/M,Bn=Kf/M;u表示电流iq,即为控制器输出。
系统内、外均存在未知扰动时,其动态方程:
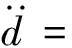
(8)
式中:C=-1/M;ΔA,ΔB,ΔC表示由动子总质量、粘滞摩擦等引起的系统不确定性;H为系统内、外部未知集总扰动,可表示:
(9)
在系统运行过程中,用正实数ρ代表未知集总扰动H的上界,满足|H|≤ρ。
2 PMLSM控制系统的设计
针对PMLSM伺服系统易受外部扰动等不确定性因素的影响,采用ANFTSMC方案来提高系统的收敛速度,并对系统中不确定因素进行有效抑制,进而提高系统的鲁棒性能。基于ANFTSMC的PMLSM伺服系统框图如图1所示。
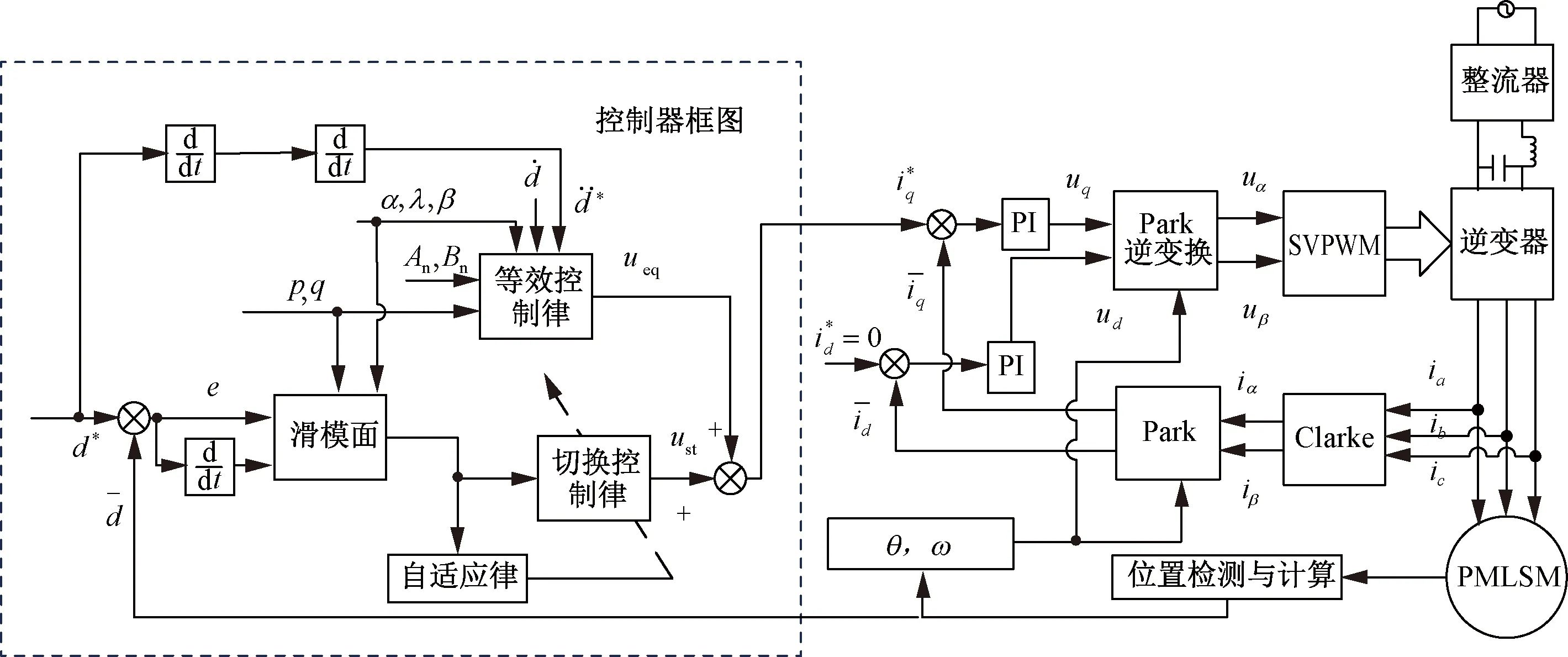
图1 基于ANFTSMC的PMLSM伺服系统框图
终端滑模控制(以下简称TSMC)与SMC进行比较,不仅继承了SMC的鲁棒性强、具有收敛性等特点,而且系统跟踪性能以及收敛时间优于SMC。取终端滑模面s:
(10)
式中:x为系统状态变量;β>0;p,q为正奇数,且满足p>q。
系统收敛至原点的时间:
(11)
系统如果能够进入滑动模态,证明整个系统是收敛的,且最终会回到原点,TSMC满足此收敛条件并且会在一定时间内收敛到原点。然而依旧存在的问题是,TSMC虽然在接近原点时收敛速度较SMC有所提高,但是在距离原点较远时,收敛速度不够快。因此,采用快速终端滑模控制(以下简称FTSMC),定义滑模面:
(12)
系统的收敛时间:
(13)
通过在TSMC的滑模面公式上设计线性项,使得在距离原点较远时,线性项起主要作用,在接近原点时,幂次项起主要作用,两者取长补短,最终只要系统进入滑动模态阶段,就会有较快的收敛时间。

(14)
式中:α,β>0,λ>1;p,q为正奇数,且满足p>q。
定义动子位置跟踪误差e:
e=d*-d
(15)
式中:d*表示给定位置信号;d表示实际位置信号。
采用NFTSMC能够改进跟踪精度,并提高趋近原点时系统的收敛速度,定义非奇异快速终端滑模面:
(16)
式中:α,β>0,λ>1;p,q为正奇数,且满足p>q。
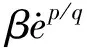
对s求导后得:
(17)
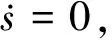
(18)
为了加强系统对外部扰动的抑制作用,设计切换控制项ust:
ust=Bn-1[ksgn(s)]
(19)
式中:sgn(s)表示符号函数;k表示切换增益。在设计中令k>0,并且满足k=ρ+η,其中,η为一正实数。通过改变k值能够削弱抖振且提高抗扰性能,使得系统整个控制性能有所提高。
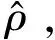
(20)
式中:c为常数。系统总控制律:
u=ueq+ust
(21)
构造李雅普诺夫函数V:
(22)
对V求导,得:
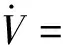
(23)
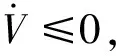
3 系统仿真分析
为了证明本文控制器的有效性,下面进行仿真阐述,分别采用SMC、NFTSMC和ANFTSMC 3种方法对PMLSM伺服系统进行仿真,PMLSM的主要参数:M=16.4 kg,B=8.0 N·s/m,Kf=50.7 N/A,ψf=0.09 Wb,p=3,Rs=2.1 Ω,Ld=Lq=41.4 mH,τ=32 mm。采用控制变量法调整控制器的参数,最优的系统控制参数如下:SMC参数,k1=2 000,k2=5,c=20;NFTSMC参数,p=7,q=5,β=0.025,α=17,λ=1.4,k=10;ANFTSMC参数,p=7,q=5,β=0.025,α=17,λ=1.4,k=10,c=100 000,η=8。
给定两种不同的输入信号,通过仿真对比说明本文控制器能满足一定的要求。
1)输入幅值为1 mm的阶跃信号,在1 s时加入100 N·m的恒定负载扰动。
图2是给定幅值为1 mm的阶跃信号下3种控制方法的位置跟踪曲线。可以看出,ANFTSMC可以快速到达给定位置,NFTSMC次之,SMC从3种曲线比较来看收敛速度较慢。由局部放大图可知,SMC的位置跟踪曲线在给定位置上下进行波动,幅度较大,NFTSMC的位置跟踪曲线在给定位置上下波动幅度比SMC小,ANFTSMC基本可以回到给定位置1 mm处,曲线波动幅度最小。通过对比可得,ANFTSMC能够提高位置跟踪精度,提高收敛速度。
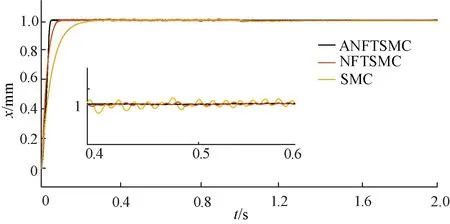
图2 阶跃信号位置跟踪曲线
在1 s突加100 N·m负载之后,局部放大图如图3所示。突加负载以后,SANFTSMC仍然在给定曲线附近波动,系统跟踪效果最好。NFTSMC则在0.99 mm~0.995 mm之间波动,跟踪精度不如ANFTSMC。SMC则在0.985 mm附近波动,跟踪精度比较差。由此说明,采用ANFTSMC方法的系统在突加100 N·m负载后跟踪效果仍然较好。
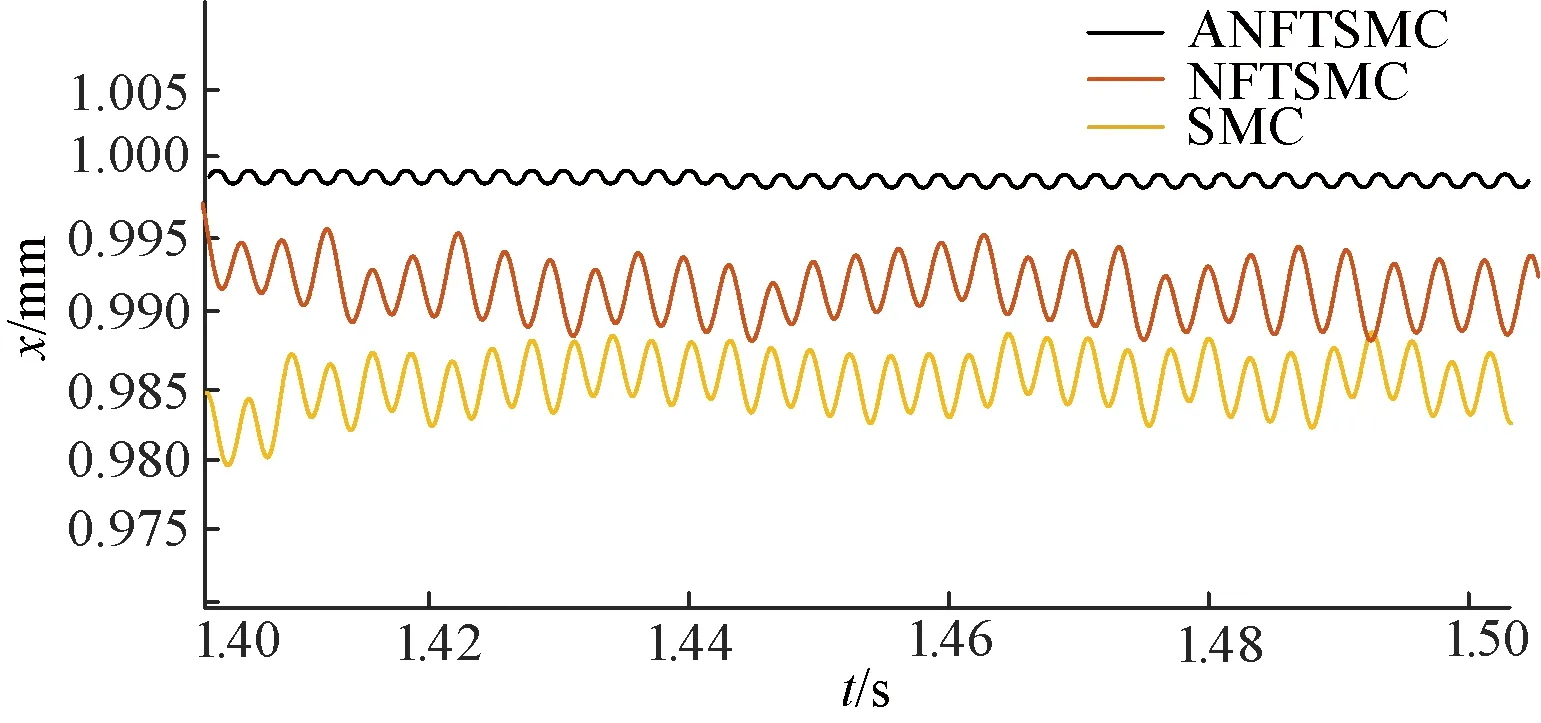
图3 阶跃信号突加负载位置跟踪曲线
3种控制方法的PMLSM伺服系统位置误差曲线如图4所示。由图4可看出,ANFTSMC优于SMC、NFTSMC,在0.05 s时系统已经达到稳定状态;NFTSMC需要约0.1 s达到稳定状态;SMC则最慢,需要约0.25 s达到稳定状态。ANFTSMC的收敛速度最快,最先达到稳定,响应速度有明显提高。
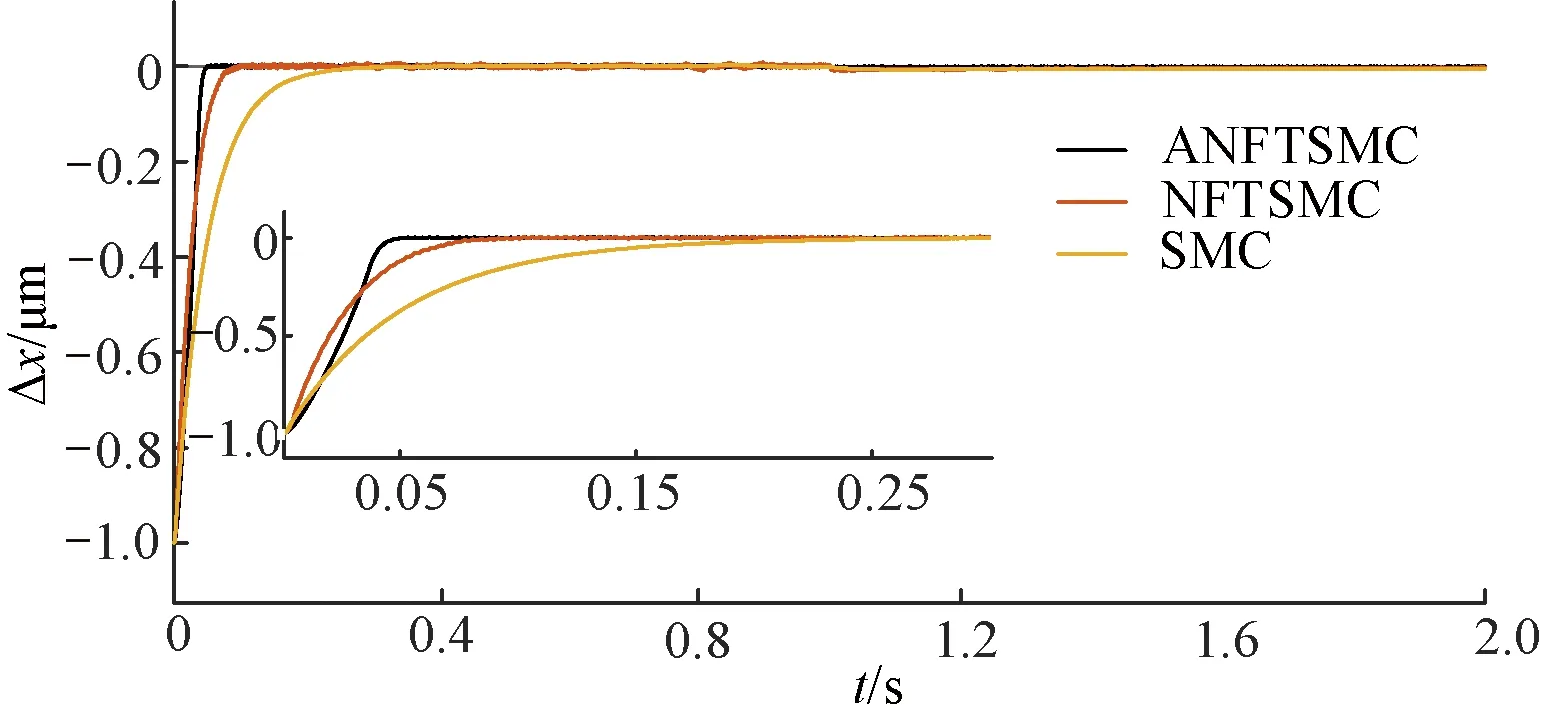
图4 阶跃信号位置误差曲线
2)给定幅值为0.2 m的正弦信号,且在1 s突加100 N·m的恒定负载扰动。
图5是给定正弦信号下3种控制方法的PMLSM伺服系统位置跟踪曲线。由图5可知,SMC的跟踪效果不及NFTSMC与ANFTSMC,但是加入自适应以后,对系统不确定性未知上界进行实时估计,ANFTSMC的跟踪效果进一步加强,同时提高了控制精度,使系统的控制性能得到改进。图6是3种控制方法的位置误差曲线。由图6可知,ANFTSMC在约0.1 s达到稳定,NFTSMC在0.14 s左右达到稳定,SMC则需要约0.3 s才到达稳定,ANFTSMC的响应速度在三者之间最好。因此再次证明采用ANFTSMC方法可以提高系统收敛速度。
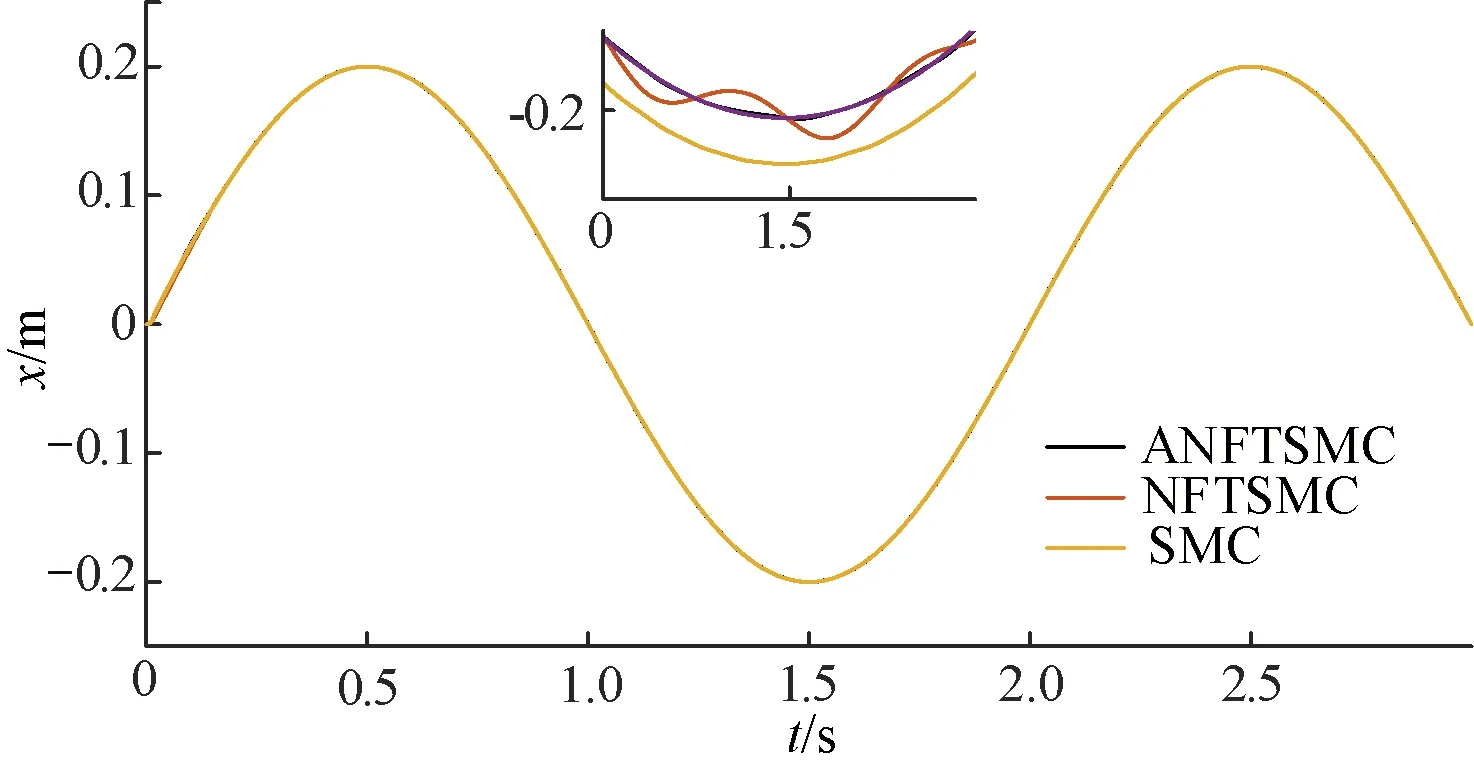
图5 正弦信号位置跟踪曲线
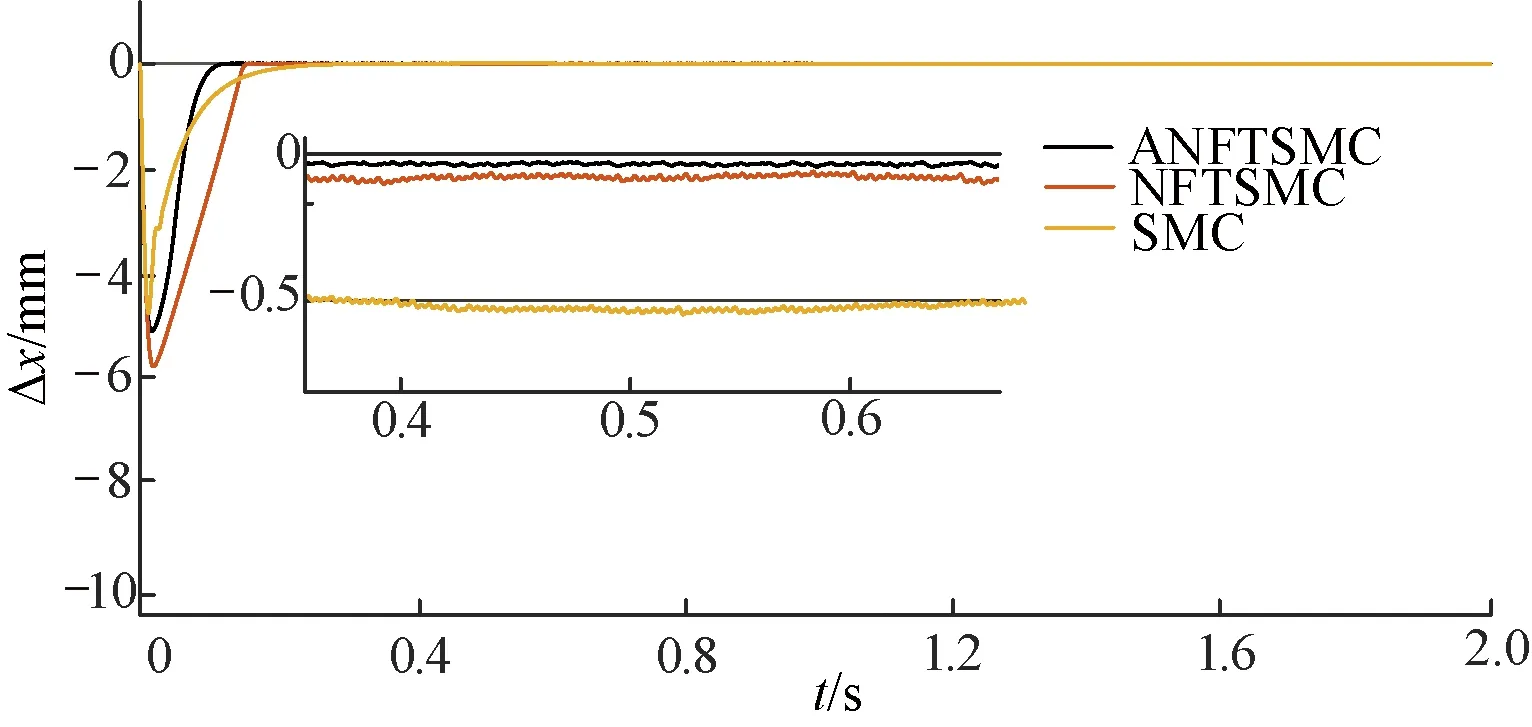
图6 正弦信号位置误差曲线
在1 s突加100 N·m负载以后,3种控制方法的位置误差曲线局部放大图如图7所示。SMC很难回到给定位置,NFTSMC的曲线在-5 μm附近波动,正弦信号位置误差曲线优于SMC。而ANFTSMC在0.3 μm~0.4 μm附近波动,在三者比较中效果最好,ANFTSMC的稳定性更好。这说明ANFTSMC的跟踪精度和鲁棒性都有所提高。
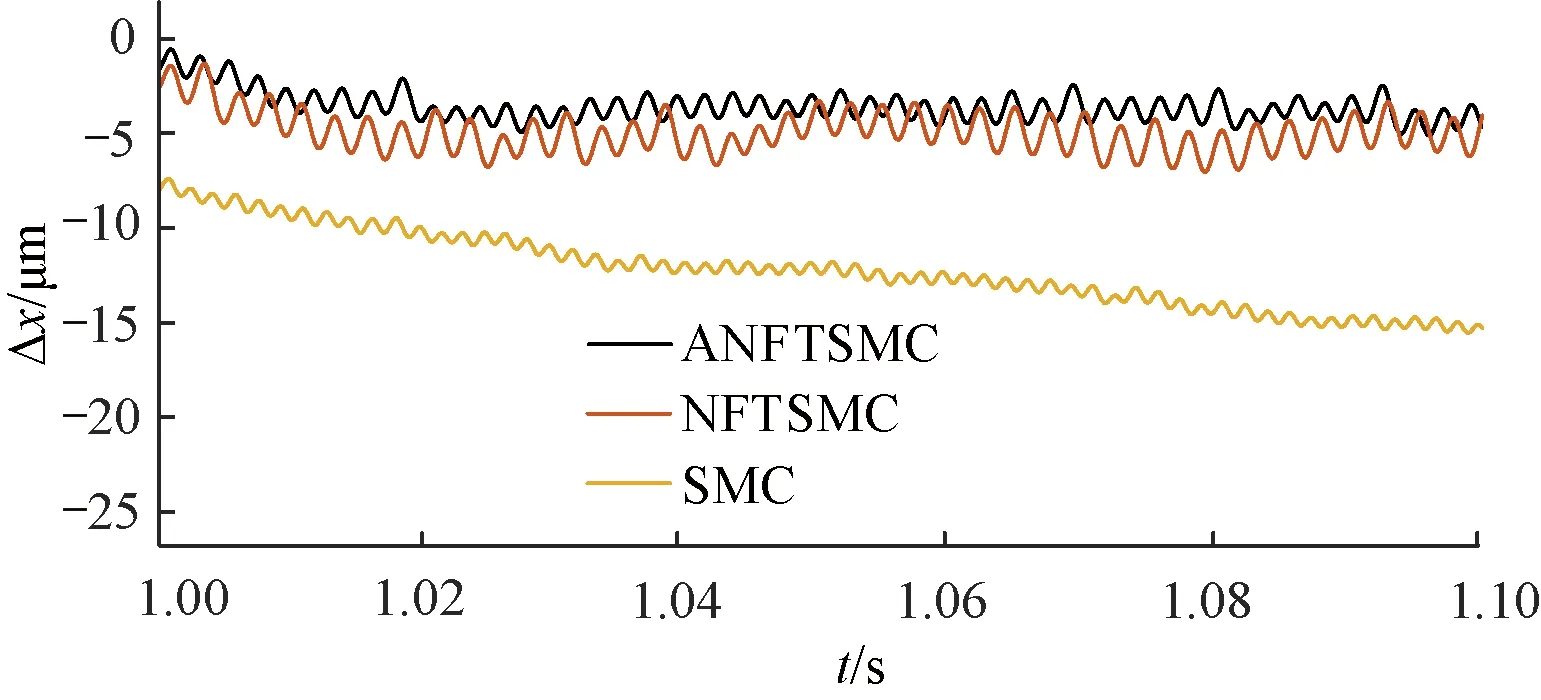
图7 正弦信号突加负载位置跟踪曲线
图8和图9分别是NFTSMC和ANFTSMC控制方法下,给定幅值为0.2 m的正弦信号伺服系统位置误差曲线局部放大图。由图8、图9可知,在到达稳态后,NFTSMC系统跟踪误差始终在4 μm左右,而ANFTSMC系统跟踪误差始终在2 μm左右,抖振现象明显得到改善,加入自适应律可在线估计系统不确定性参数的上界。
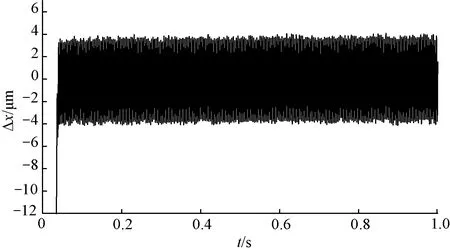
图8 NFTSMC位置误差曲线
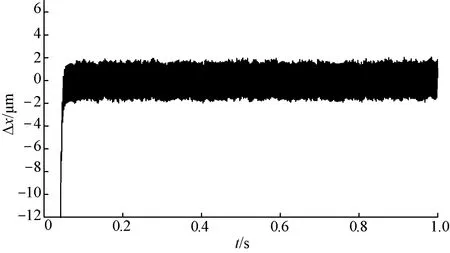
图9 ANFTSMC位置误差曲线
4 结 语
针对PMLSM采用传统SMC进行位置控制时,存在收敛时间慢、抗扰性差、位置跟踪精度低等问题,本文提出了ANFTSMC方法,在传统SMC上加入非奇异快速终端项,系统不仅能够在有限时间内收敛,避免了奇异性,而且提高了系统的控制性能。为进一步增强系统的鲁棒性和跟踪精度,在NFTSMC的基础上加入自适应律,用以估计系统所受不确定性的上界。仿真结果验证了本文控制方法的有效性。
