高功率密度永磁同步电机永磁体涡流损耗分布规律及其影响

陈 萍 唐任远 佟文明 贾建国 段庆亮

（沈阳工业大学国家稀土永磁电机工程技术研究中心 沈阳 110870）

1 引言

与传统电励磁电机相比，永磁同步电机具有损耗小、效率高，体积小，运行可靠等优点[1]。电机电磁场包括许多谐波：磁导谐波，磁场空间谐波和电流时间谐波。这些谐波在电机中产生的损耗不容忽视，特别是在变频器供电的永磁同步电机中，谐波含量大，钕铁硼永磁体电导率高，会引起较大的永磁体涡流损耗。相对于铜耗和铁耗来说，永磁体涡流损耗并不大，但由于高功率密度永磁同步电机体积小、散热差，特别是转子部位，足以产生过热的温升导致永磁体失磁，威胁电机运行的安全性与可靠性。随着永磁同步电机应用范围的扩大，永磁体涡流损耗的研究已成为永磁同步电机领域最为重要的关键技术之一。

2D有限元法计算永磁体涡流损耗时，将永磁体等效为一根两端绝缘的短路导体，这样永磁体两端的电压为零。使用 2D有限元法计算永磁体涡流损耗时，认为永磁体的轴向长度要远大于永磁体的宽度，因而无法计及永磁体涡流损耗轴向分布的不均匀[2,3]，这样计算得到的永磁体涡流损耗并不准确[4]。虽然3D有限元计算要占用大量的时间和计算机资源，但是建立三维模型，进行 3D有限元计算仍是解决这一问题的良好方法。

Yamazaki K.等人使用3D有限元法对永磁体涡流损耗分布进行分析[5,6]，但是缺少对永磁体涡流损耗必要的理论分析且也没有对永磁体涡流损耗的分布规律进行研究。

对永磁同步电机的温度场进行研究的文献，永磁体热源的施加几乎都没有考虑到永磁体损耗的分布特点[7,8]。文献[9]指出永磁体涡流损耗是导致电机转子发热的主要原因，但其虽分析了电机其他部位的最大温升点出现的位置，却并没有分析永磁体最大温升点出现的位置。文献[10]对永磁体过热退磁进行了研究，其温度场计算同样也是只将永磁体的平均损耗分布施加于永磁体上来计算温升，且并没有指出永磁体的局部最热点的具体位置。

得知永磁体局部最热点，则可有针对性地对永磁同步电机结构进行改进，消除局部最热点，优化电机设计。这就要求对永磁同步电机的永磁体涡流损耗及其分布以及对永磁体温升分布的影响进行深入的分析。

本文以一台 2.1kW 永磁同步电机为例进行 3D电磁场有限元分析，对产生永磁体涡流损耗的三个因素进行了计算，并给出了永磁体涡流损耗的三维分布图，同时对不同轴向长度永磁体的涡流损耗分布规律进行了量化分析。将永磁体涡流损耗分块平均分布值与永磁体涡流损耗整块平均分布值分别代入 3D温度场进行温升计算，分析永磁体局部温升最热点出现的位置。并将永磁体涡流损耗的各个方向的分布代入温度场进行计算，分析哪个方向的永磁体涡流损耗对温升分布的影响最大。最后，通过温升实验来验证温度场计算的准确性。

2 永磁体涡流损耗分布的理论分析

对永磁体涡流损耗的分析，数值上的准确计算固然重要，但是其分布规律也同样不容忽视。

永磁体涡流损耗可由以下公式计算[11]

建立图1所示的永磁体涡流损耗计算模型。该模型中，永磁体的长为l，宽为w，厚为h。本文研究坐标在（x,y）处的某回路（见图 1中阴影）。此回路x方向的宽度为dx，y方向的宽度为dy。

图1 永磁体涡流损耗计算模型Fig.1 The calculation model of PM eddy current loss

根据法拉第电磁感应定律

由于E=ρJ，得

式中φ——涡流路径所包围的磁通；

S——涡流路径所包围的面积。

当永磁体的涡流路径取模型中路径时，由式（3）可得

因此，由式（4）得

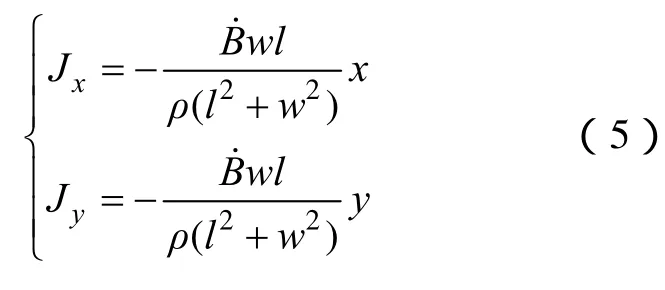
由式（5）可知，永磁体涡流密度的分布与永磁体上磁通密度变化、永磁体电阻率、永磁体形状以及所处永磁体上的位置有关。

3 永磁体涡流损耗及其分布规律的3D有限元仿真分析

本文采用 3D有限元对永磁体涡流损耗的数值和分布规律进行分析。

3.1 电磁场计算模型

以一台 2.1kW 表面式永磁同步电机为例进行3D有限元分析。该 2.1kW电机永磁体表面无金属护套，使用无纬玻璃丝绑扎。本文建立其 1/4周期模型，即取1个单元电机进行分析，其剖分图如图2所示。2.1kW永磁同步电机的永磁体结构型式为表面式，平行充磁，8极36槽，额定频率为266.7Hz，额定转速为 4 000r/min。进行电磁场计算的电流波形为实测波形，经滤波后的波形如图3所示。

图2 2.1kW永磁同步电机剖分图Fig.2 Grid map of 2.1kW PMSM

图3 2.1kW永磁同步电机PWM供电时的电流波形Fig.3 The waveform of 2.1kW PMSM under PWM supply

为了在计算永磁体涡流损耗大小的同时，得到永磁体涡流损耗的分布特性，本文对永磁体进行了一些特殊处理：将每块永磁体沿轴向分为10段，周向分为6段，厚度方向上分为3层，如图4所示。因为没有对任何两块永磁体之间施加边界条件，因此这180块永磁体合起来仍与一整块永磁体等效。

图4 永磁体涡流损耗计算模型分块示意图Fig.4 Diagram of PM eddy current loss calculation model

3.2 永磁体涡流损耗的产生因素分析

本文从产生因素角度将永磁体涡流损耗分为：①由于定子铁心开槽导致的磁导谐波产生的永磁体涡流损耗；②定子绕组分布，基波电流导致的空间谐波磁场产生的永磁体涡流损耗；③定子电流时间谐波产生的永磁体涡流损耗。

图5和表1分上、中、下三层，从产生永磁体涡流损耗的各个因素角度对永磁体涡流损耗分布进行了分析。磁导谐波、基波电流产生的空间谐波磁场和时间谐波电流三种因素产生的永磁体涡流损耗分布都是上层永磁体的大，占总体永磁体涡流损耗的 42.27%，这主要是由于上层永磁体暴露在气隙磁场中，开槽对其影响要比中、下层的大，同时由于透入深度的问题，电流时间谐波对永磁体涡流损耗的影响也主要集中于永磁体上层。通过分析也可看出，时间谐波电流是产生永磁体涡流损耗的主要因素，而这主要是因为该2.1kW永磁同步电机变频器供电的电流时间谐波含量大的缘故，如图 3所示。

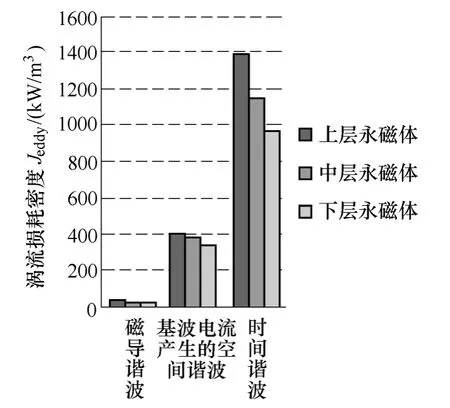
图5 各个因素产生的永磁体涡流损耗密度Fig.5 Eddy current loss density of each origin

表1 上、中、下三层永磁体涡流损耗占总永磁体涡流损耗的百分比（%）Tab.1 The percentage of upper, middle and lower PM eddy current loss in the total eddy current loss

图 6～图 8分别为各个因素在一个极下的永磁体涡流损耗分布。从这3幅三维图中可以明显看到，永磁体涡流损耗在永磁体中分布的总体趋势是四周大，中间小，四个端点的永磁体涡流损耗小。其中，磁导谐波产生的永磁体涡流损耗四个端点特别小。

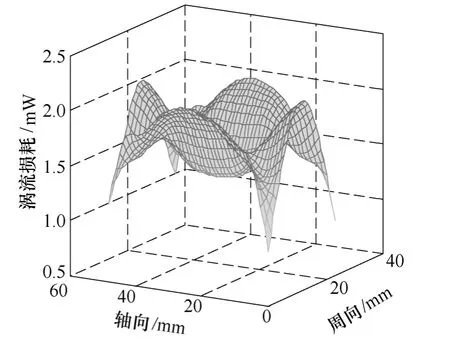
图6 磁导谐波产生的永磁体涡流损耗分布图Fig.6 The distribution of PM eddy current loss caused by permeance harmonics

3.3 永磁体涡流损耗的分布规律分析

本文所分析的2.1kW电机每个永磁体长55mm，宽28.17mm。保持电机整体结构型式不变，只对电机的轴向长度进行改变，分别取轴向长度为88mm、66mm、44mm、33mm、22mm，与本文的轴向长度55mm进行对比，分析永磁体长宽的改变对永磁体涡流损耗分布规律的影响，如图9所示。

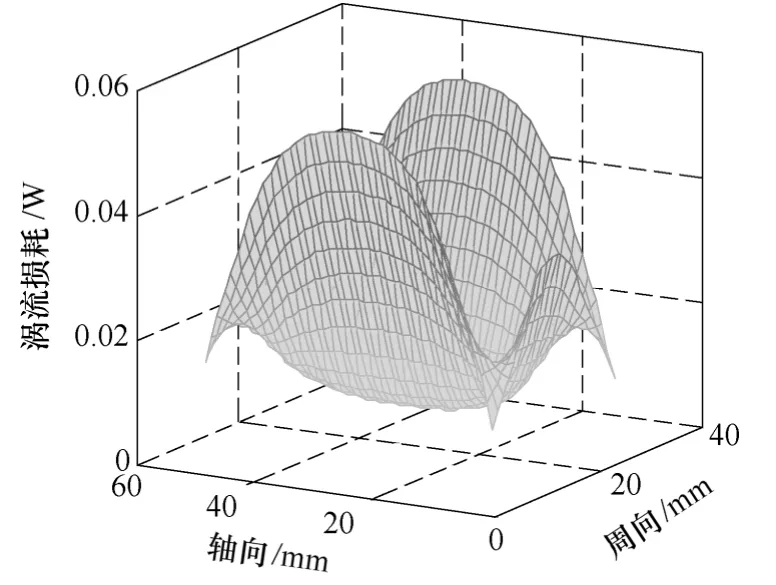
图7 基波产生的空间谐波导致的永磁体涡流损耗分布图Fig.7 The distribution of PM eddy current loss caused by spatial harmonics due to fundamental wave

图8 时间谐波产生的永磁体涡流损耗Fig.8 The distribution of PM eddy current loss caused by time harmonics

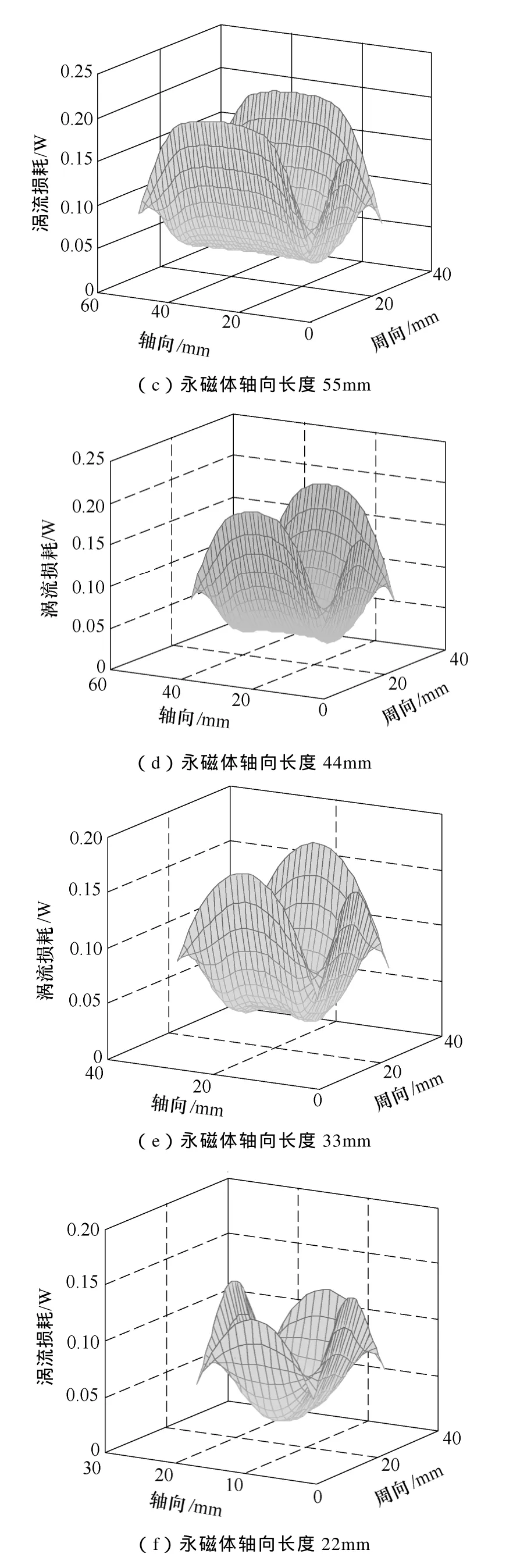
图9 永磁体涡流损耗分布随永磁体轴向长度的变化Fig.9 The distribution of PM eddy current loss vs.the axial length of PM

从图9可以看到，永磁体轴向长度为88mm时，永磁体涡流损耗的最大值出现在轴向边线上。随着永磁体长度变得越来越短，永磁体轴向边线中部永磁体涡流损耗较为平缓的部分越来越短，永磁体涡流损耗最大值越来越接近周向边线的最大值，直至当永磁体轴向长度为22mm时（小于周向长度28.17mm），永磁体涡流损耗的最大值被周向边线上的最大值所替代。由图9的6种永磁体长度下的永磁体涡流损耗的分布可以看出，每个极的永磁体涡流损耗的最大值出现在永磁体长和宽中长度比较大的那条边线上，且永磁体涡流损耗变化较大的部位为边线两端。当永磁体轴向长度足够长时，轴向中间部位的磁通密度变化很小，从而导致轴向中间部位的永磁体涡流损耗变化平缓。这与式（5）的分析相吻合。由式（4）、式（5）可以看出，永磁体涡流损耗密度的最大值出现在x、y中最大的部位，这而这个部位就是永磁体长、宽边线中较大者的中部。

同时由于Jy=(w/l)Jx，所以永磁体涡流损耗分布的最大点取决于永磁体的形状。

表2 永磁体轴向和周向边线永磁体涡流损耗最大值Tab.2 The maximum eddy current loss value of PM axial and circumferential edge

图10 永磁体涡流损耗轴向边线最大值随轴向长度占轴向与周向长度和比例的变化Fig.10 The variation of the maximum eddy current loss of the PM axial edge vs. the percentage of axial length to the sum of axial length and circumferential length

表2给出了这6个永磁体轴向长度所对应的永磁体轴向和周向边线的最大值。从表2和图10可以看出，永磁体涡流损耗在轴向边线的最大值随着轴向长度比例（本文指轴向长度占轴向与周向长度和的比例）的增大而变大，但是变大趋势逐渐平缓。可以设想，当永磁体轴向长度远大于周向长度时，永磁体涡流损耗的数值在轴向方向将不变，但这在实际问题中是不存在的情况，而 2D有限元法计算永磁体涡流损耗正是基于此假设，因此计算出来的永磁体涡流损耗误差较大。

本文用一个分段函数来量化图 10所示的永磁体涡流损耗轴向边线最大值Peam随轴向长度比例β的关系，如式（6）所示。这种分段函数的定量分析方法比单纯定性分析更能揭露永磁体涡流损耗规律的本质。

3.4 涡流密度线概念

基于以上的分析，本文运用涡流密度线的概念来更好地理解永磁体涡流损耗的分布。如图11所示的一个周期内的平均涡流密度线有以下特点：

图11 永磁体涡流线分布示意图Fig.11 The sketch map of PM eddy current density lines

（1）涡流密度线为闭合的曲线。

（2）涡流密度线互相之间不相交。

（3）涡流密度线越密的地方涡流损耗越大。

（4）涡流密度线有“端部效应”，即越靠近永磁体端部边线永磁体涡流密度线越密集，永磁体涡流损耗越大。

这就解释了为什么端部边线上的永磁体涡流损耗大，中间部位的永磁体涡流损耗小。同时对角线部位的永磁体涡流损耗应该是最小的，因为对于矩形永磁体来说，对角线的永磁体涡流密度线最稀疏，永磁体涡流损耗最小。

4 永磁体涡流损耗分布对永磁体局部最热点影响的研究

4.1 温度场计算模型

对 2.1kW 永磁同步电机的热计算模型进行简化，以便节约计算时间、加密计算模型。本文建立该电机的1/4模型，即2个极模型，其模型剖分图如图12所示。该电机各部位的损耗值见表3。

图12 2.1kW永磁同步电机温度场计算模型剖分图Fig.12 Thermal field calculation model grid map of 2.1kW PMSM

表3 2.1kW永磁同步电机各部位损耗值Tab.3 Loss of each part in 2.1kW PMSM（单位：W）

不同的冷却系统结构、不同的表面特性、不同的冷却介质及其流速都会对电机内各表面的对流散热系数有所影响。本文所分析的2.1kW永磁同步电机属于机壳自然通风散热，机壳表面的对流散热系数参照文献[12]取为 14.2W/(m2·K)。

表4给出了2.1kW永磁同步电机大部分材料的导热系数，其中定转子叠片铁心为各向异性材料，z方向即为其叠压方向。

表4 2.1kW永磁同步电机材料的导热系数Tab.4 The thermal conductivity of materials in 2.1kW PMSM（单位：W/(m·K)）

4.2 温升分布分析

在其他条件都相同的情况下，对不同情况下永磁体涡流损耗的分布情况进行温度分布计算，分别为：

（1）永磁体涡流损耗分块平均分布，即每块的涡流损耗值平均分布在这块永磁体上。

（2）永磁体涡流损耗整块平均分布，即整个永磁体（永磁体不分块）的涡流损耗平均分布在这个永磁体上。

环境温度为19℃，得到的永磁体温度分布对比图如图13所示，2.1kW永磁同步电机总体的温度分布对比图如图14所示。从这两幅图中可以看出，永磁体涡流损耗的分布对电机其他部位的温升分布影响不大，但却对自身的温升分布影响很大。

图13 2.1kW永磁同步电机永磁体温度分布图Fig.13 PM temperature distribution of 2.1kW PMSM

图14 2.1kW永磁同步电机总体温度分布图Fig.14 The total temperature distribution of 2.1kW PMSM

从图14可以看出，该永磁同步电机永磁体发热特别严重，由于转子的散热不好，永磁体温升是整个电机温升中最大的。从图13可以看出，虽然由于电机前端与后端结构的不同，导致电机永磁体温度并非沿轴向对称分布，但是实际上永磁体局部最热点出现在永磁体涡流损耗最大点的附近，而非永磁体涡流损耗整块平均分布时的永磁体中间部位。

这就得出一个结论，对于本文这种高功率密度、体积小的永磁同步电机，永磁体上的温升特别高，若发生退磁，则最易退磁的地方应该是永磁体表面、轴向中部、周向两边部位，即永磁体涡流损耗分布最大值出现的位置附近。

4.3 永磁体局部最热点的简化分析

本文将每个永磁体分成180块的方法虽然能够较为准确地得到永磁体局部最热点的温度值及分布位置，但是在工程计算中，这种方法无论是对电磁场计算还是温度场计算都相当麻烦。为此，本文将对永磁体涡流损耗各个方向的分布规律对局部最热点的影响进行研究。

图15为永磁体涡流损耗周向分段平均分布、轴向分段平均分布、径向分层平均分布及分圈平均分布（见图4的3圈）对永磁体温度分布的影响。与图13进行对比分析，可见，当只考虑永磁体涡流损耗的周向分段平均分布时，永磁体温度分布和永磁体涡流损耗分块平均分布时温度分布规律相近、数值相当。为了更快地计算永磁同步电机的永磁体温升数值以及温升分布，对于本文这种轴向长于周向的永磁体，以后的计算中可以不需将永磁体分为180块，而只需将永磁体周向分段进行电磁场和温度场的计算即可得到与整体分块计算相似的结果。

图15 永磁体涡流损耗分布对永磁体温度分布的影响Fig.15 The effect of PM eddy current loss distribution to its temperature distribution

4.4 温升实验及数据比较

表5给出了2.1kW永磁同步电机各部位的温升分布对比。实验之初，在永磁体端部贴上了英国厄麦德公司的Thermal 8型号温度贴片（实际测温点在永磁体轴向端部位置），绕组端部埋置了热电阻，轴温采用光电式温度计进行测量。其中，轴的测量点在靠近端盖的部位。测点示意图如图16所示。表3给出了不同永磁体涡流损耗分布时温升分布的对比，实验时室温为19℃。由表5的对比可知，永磁体涡流损耗的分布对永磁同步电机整体温升的分布影响并不大，只是对永磁体局部最热点的数值和出现的位置影响比较大。表5的数据同时也验证了本文损耗和温升计算的准确性。

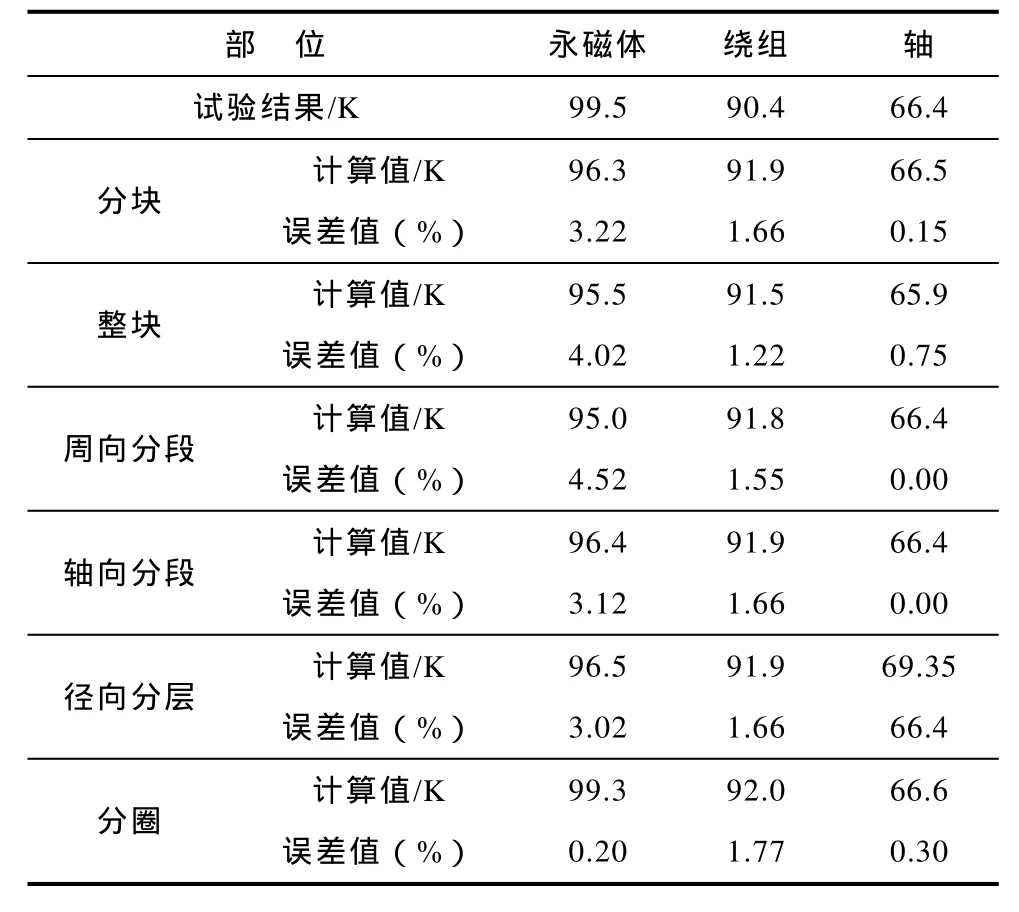
表5 2.1kW永磁同步电机不同永磁体涡流损耗分布时温升对比Tab.5 Temperature rising comparison of 2.1kW PMSM with different PM eddy current distribution

图16 2.1kW永磁同步电机实际测温点示意图Fig.16 Sketch map of actual temperature measuring point in 2.1kW PMSM

5 结论

本文结合理论分析，使用三维电磁场对永磁体涡流损耗的分布进行了研究，并通过三维温度场分析永磁体涡流损耗分布对永磁同步电机永磁体温升分布的影响。得到如下六个结论：

（1）永磁体涡流损耗在永磁体中分布的总体趋势是表面大、四周大，中间小，四个端点的永磁体涡流损耗小。

（2）从产生因素角度分析，时间谐波是变频器供电永磁同步电机永磁体涡流损耗产生的主要因素。

（3）永磁体涡流损耗的分布受永磁体形状的影响，最大永磁体涡流损耗的位置在永磁体轴向和周向较长的边线上。

（4）通过涡流密度线，能够非常好的理解永磁体涡流损耗的分布特性。

（5）通过永磁体涡流损耗分块平均分布的方式确定了永磁体局部温升最热点在永磁体涡流损耗最大点附近，而非永磁体中间部位。

（6）对于轴向长度大于周向长度的永磁体，永磁体涡流损耗的周向分段平均分布是替代分块平均分布的更适用于工程计算的方法。

[1] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2006.

[2] Wu L J, Zhu Z Q, Staton D, et al. Analytical model for predicting magnet loss of surface-mounted permanent magnet machines accounting for slotting effect and load[J]. IEEE Transactions on Magnetics,2012, 48(1): 107-117.

[3] Niu S, Ho S L, Fu W N, et al. Eddy current reduction in high-speed machines and eddy current loss analysis with multislice time-stepping finite-element method[J]. IEEE Transactions on Magnetics, 2012, 48(2):1007-1010.

[4] Martin F, Zaim M, Tounzi A, et al. Improved analytical determination of eddy current losses in surface mounted permanent magnets of synchronous machine[J]. IEEE Transactions on Magnetics, 2014, 50(6): 1-10.

[5] Yamazaki K, Abo A. Loss investigation of interior permanent-magnet motors considering carrier harmonics and magnet eddy currents[J]. IEEE Transactions on Industry Applications, 2009, 45(2): 659-665.

[6] Yamazaki K, Fukushima Y, Sato M. Loss analysis of permanent magnet motors with concentrated windings—variation of magnet eddy current loss due to stator and rotor shapes[C]. IEEE Industry Applications Society Annual Meeting, 2008: 1-8.

[7] 孔晓光, 王凤翔, 邢军强. 高速永磁电机的损耗计算与温度场分析[J]. 电工技术学报, 2012, 27(9):166-172.

Kong Xiaoguang, Wang Fengxiang, Xing Junqiang.Losses calculation and temperature field analysis of high speed permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2012, 27(9):166-172.

[8] 黄允凯, 胡虔生, 朱建国. 顾及旋转铁耗的高速爪极电机三维磁热耦合分析[J]. 电工技术学报, 2010,25(5): 54-60.

Huang Yunkai, Hu Qiansheng, Zhu Jianguo. Magnetothermal analysis of a high-speed claw pole motor considering rotational core loss[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 166-172.

[9] 付兴贺, 林明耀, 徐妲, 等. 永磁-感应子式混合励磁发电机三维暂态温度场的计算与分析[J]. 电工技术学报, 2013, 28(3): 107-113.

Fu Xinghe, Lin Mingyao, Xu Da, et al. Computation and analysis of 3D-Transient temperature field for a permanent magnet-induction hybrid excitation generator[J]. Transactions of China Electrotechnical Society,2013, 28(3): 107-113.

[10] 师蔚. 高密度永磁电机永磁体防退磁技术的研究:[D]. 上海: 上海大学, 2012.

[11] 倪光正. 工程电磁场原理[M]. 北京: 高等教育出版社, 2002.

[12] 陈世坤. 电机设计[M]. 北京: 机械工业出版社,2000.