基于超螺旋观测器的SPMSM无传感器控制

杨贽玮,赵世伟,杨向宇,邱小华

(华南理工大学 电力学院,广州 510640)

0 引 言

表贴式永磁同步电机(以下简称SPMSM)具有结构简单、可靠性高、功率密度高等优势,近年来广泛应用于高性能调速系统[1]。其调速系统的控制方式有矢量控制和直接转矩控制,前者性能更优异,在实际应用中更加广泛[2]。矢量控制要求电机反馈准确的转子位置,其获取通常依靠加装在电机转轴上的机械位置传感器,继而带来了系统可靠性降低、体积增大和成本增加的问题。无传感器控制通过采样电机电信号来估计转子位置,避免了使用位置传感器[3]。目前,永磁同步电机无传感器控制已经成为国内外学者研究的热点[4]。

无传感器控制的主要方案有Luenberger观测器、滑模观测器、模型参考自适应和卡尔曼滤波等。其中,滑模观测器(以下简称SOM)有实现简单和抗扰强的优势,但其观测反电动势由高频开关信号组成,导致了波形正弦度低以及严重的抖振现象[5]。

文献[6]在传统SMO的基础上使用sigmoid函数替代sign函数,有效减小了抖振。对观测反电动势进行滤波可以显著提高其正弦度,但会引入相位滞后问题。文献[7]使用滤波后的反电动势代替滤波前抖动严重的反电动势信号作为滑模观测器的反馈,改善了滤波环节造成的相位滞后。文献[8]中,为了避免使用低通滤波器,设计了状态观测器观测反馈信号,该方法实现了较宽的调速范围,但状态观测器的设计与参数设置较复杂。文献[9]设计了基于饱和函数的滑模观测器,引入一种截止频率随转子速度变化而变化的低通滤波器,改善了滤波效果,但由于传统滑模的局限,观测位置仍有一定的抖动。文献[10]引入模糊规则,对超螺旋观测器(以下简称STO)参数进行在线整定,提高了观测器在参数变化情况下的鲁棒性,但模糊规则的设计较困难。文献[11]提出了一种变增益STO,观测器增益与电机转速相关,减小了低速时的观测误差。

针对SMO的抖振问题,本文设计了STO并对观测反电动势进行滤波以削弱高次谐波,设计锁相环提取转子位置和转速信号并对转子位置进行补偿,以减小滤波带来的相位滞后。最后进行仿真与实验以验证本方案的有效性。

1 SPMSM数学模型

SPMSM在α-β坐标系下的数学模型如下:

(1)

式中:uα、uβ,iα、iβ为α-β坐标系下电压、电流;R和L为定子电阻和电感;ψm为永磁体磁链;ωe、θ为电角速度和电角度。

反电动势表达式:

(2)

式中:eα和eβ为α-β坐标系下的反电动势。

由式(2)可以得到,SPMSM反电动势中包含了电机转速和转子位置信息。

2 超螺旋滑模观测器设计

2.1 超螺旋算法

针对传统SMO固有的抖振问题,文献[12]提出了超螺旋滑模算法理论,文献[13]利用李雅普诺夫第二法证明了基于该算法的观测器在有扰动和无扰动情况下都可以在有限时间收敛。本文的超螺旋算法表示:

(3)

取δ≥0,并假设系统扰动全局有界:

(4)

当增益满足:

(5)

x=0是全局渐进平衡点,且对于任意初始状态系统将在有限时间收敛至平衡点。

2.2 基于超螺旋算法的滑模观测器

由式(1)、式(2)建立以反电动势形式表示的SPMSM方程:

(6)

电流估计方程表示:

(7)

将式(7)与式(6)作差得到电流误差方程:

(8)

(9)

基于超螺旋算法设计反电动势估计值:

(10)

观测反电动势由两项组成,前项类似于传统滑模,但会随着电流误差收敛而逐渐减小,后项是一个连续的积分项。

对照式(3)、式(7)可得:

(11)

由式(4)得:

(12)

从式(12)选定合适的δ≥0后,观测器增益k1、k2应该满足式(5)的约束,以保证收敛性能。

3 基于锁相环的转子位置估计

3.1 基于锁相环的转子位置重构

观测反电动势中包含了转子位置信息。传统方法一般使用反正切函数计算角度,再对角度微分获得角速度。即:

(13)

观测反电动势由高频信号组成,当其过零时,反正切函数会出现饱和现象,导致估计转子位置和转速出现较大的误差。为了避免这个问题,本文设计锁相环(以下简称PLL)提取转子位置信息。

PLL结构如图1所示。

图1 PLL结构图

结合式(2)可以得到:

(14)

从而得到传递函数:

(15)

通过式(15),可以使用配置带宽的方式选择PLL的PI参数。

3.2 反电动势滤波以及转子位置自适应补偿

滤波补偿框架如图2所示。

图2 滤波补偿框架图

输入PLL的反电动势表示:

(16)

式中:ωc为截止频率;ω为反电动势频率。

反电动势经过低通滤波后,相位滞后:

(17)

对应的观测角度滞后值:

(18)

补偿后的电角度:

(19)

4 仿真与实验结果

4.1 仿真分析

为了验证本文算法的可行性,在MATLAB/Simulink中搭建如图3所示的仿真模型。同时,搭建了传统SMO+PLL模型用于对比。

图3 仿真模型结构框图

图3中的PLL为锁相环,LPF为低通滤波器。STO算法框架如图4所示。在仿真过程中,设置观测器增益k1=25,k2=3 000,PLL比例积分环节Kp=900,Ki=160 000。

图4 STO算法结构

仿真电机模型参数如表1所示。

表1 仿真电机参数模型

首先,验证观测器的反电动势观测性能以及位置和转速观测效果,观测器不参与闭环,实际位置信号由电机模型提供。初始转速为750 r/min,在1 s时,转速指令阶跃为1 200 r/min。图5为STO观测反电动势波形。图6为传统SMO+PLL观测反电动势波形。

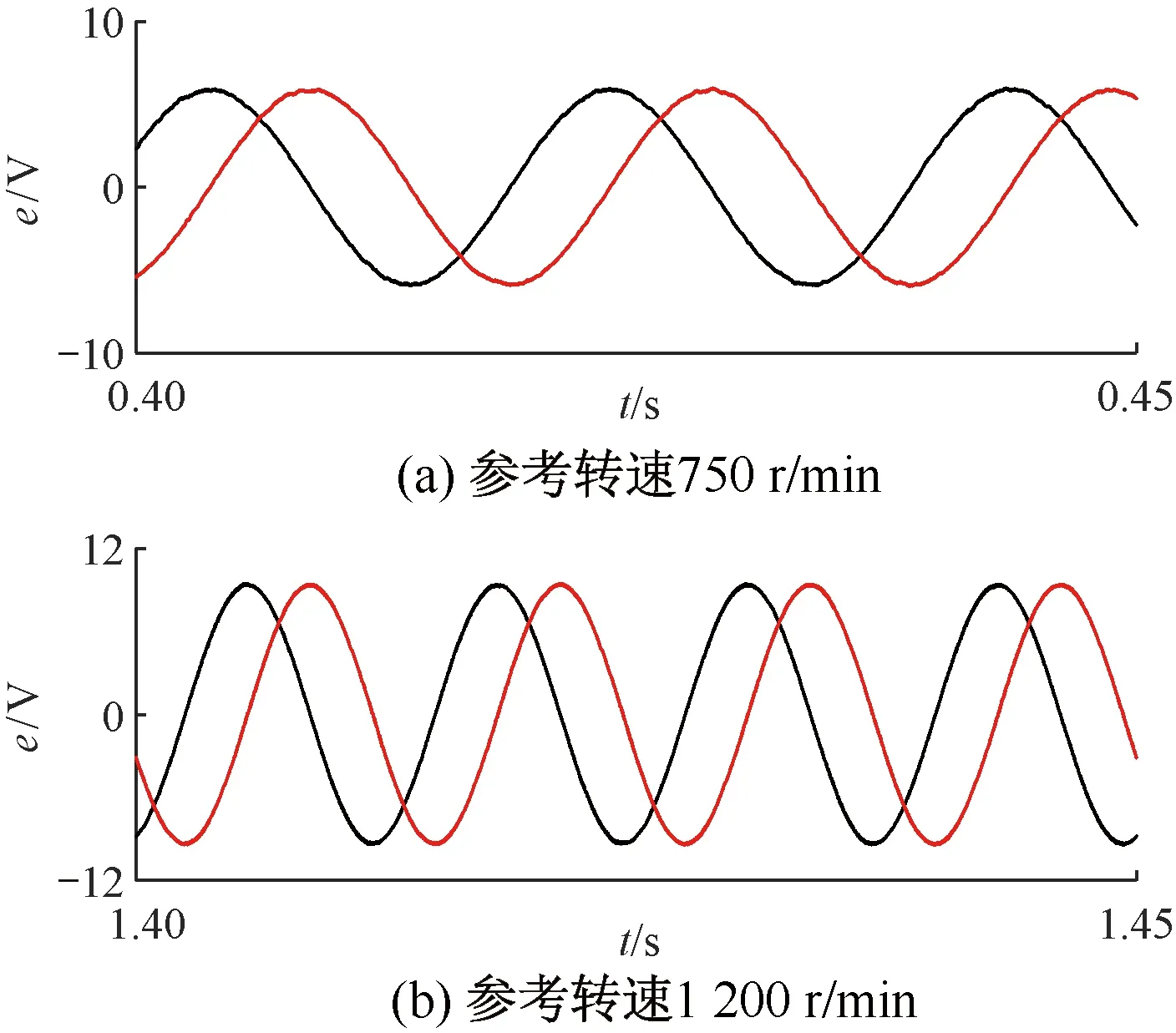
图5 STO观测反电动势仿真

图6 传统SMO+PLL观测反电动势仿真

图5和图6中,在相同滤波参数下,STO观测反电动势抖振现象好于传统SMO+PLL方案,且有更高的正弦度。转速750 r/min时,前者反电动势THD为1%,后者为4.1%;转速1 200 r/min时,前者反电动势THD为0.74%,后者为2.48%。

图7和图8为两种方案观测位置与实际位置对比,图9为两种方案观测角度误差对比。

图7 STO+PLL转子位置估计仿真

图8 传统SMO+PLL转子位置估计仿真

图9 转子位置误差仿真对比

图9中,STO方案位置误差抖动相对于传统SMO方案更小。

图10为两种方案开环转速响应曲线。图11为两种方案在两种转速情况下的对比。

(a)STO

图11 两种观测器观测转速对比

图11中,STO的观测转速波动小于传统SMO+PLL。转速750 r/min时,前者观测转速误差约为±5 r/min,后者约为±9 r/min;转速1 200 r/min时,前者观测转速误差约为±4 r/min,后者约为±7 r/min。

在电机1 200 r/min稳定运行时,加0.5 N·m负载,电机的转速响应曲线如图12所示。可以看出,观测器在加载情况下速度跟踪效果较好。

进行梯形加减速仿真,控制模型改为由观测器提供的位置和转速信号闭环。电机初始转速750 r/min,速度指令在1 s内匀加速至1 200 r/min,后在1 s内匀减速至750 r/min,得到系统的闭环转速响应曲线如图13所示。

图13 STO梯形加减速仿真

观测器全过程观测效果良好,抗速度扰动能力强。

4.2 实验分析

实验硬件平台如图14所示。控制器主控芯片使用STM32F446,功率部分采用由三个半桥驱动芯片驱动的三相全桥拓扑,直流电压24 V。电流环频率10 kHz,使用霍尔电流传感器采样A、C两相电流。转子实际位置由编码器提供。上下位机通讯使用串口协议。

图14 实验平台

首先进行阶跃实验,观测器不参与闭环。参考转速由0阶跃到750 r/min再到1 200 r/min。图15为观测反电动势波形。图16为观测位置与实际位置对比。图17为转速响应曲线。

图15 STO观测反电动势实验波形

图16 STO观测位置与实际位置实验波形

图17 STO阶跃实验转速响应

由图15可见,反电动势波形正弦度较好。图16中,观测位置与实际位置重合度较高。图17中,观测器在中高转速情况下观测转速误差均较小。

进行加载实验,观测器不参与闭环。设置参考转速为1 200 r/min,在速度稳定后加0.5 N·m负载。图18为速度响应曲线。从图18可以看出,观测器在加载时速度跟踪效果较好。

图18 STO加载实验

观测器进行闭环实验时,系统先在编码器闭环条件下运行至750 r/min,然后切换到观测器闭环。经观测器闭环后,参考转速首先保持750 r/min,后匀加速至1 200 r/min,后匀减速至750 r/min,其运行效果如图19所示。

图19 STO梯形加减速实验

由图19可见,STO在电机加减速过程中跟踪良好。

5 结 语

本文基于超螺旋算法设计SMO,采用PLL得到电机转子位置并进行自适应补偿。仿真和实验验证了该观测器的有效性。本文主要有以下结论:

(1)本文基于超螺旋算法的观测器相较于传统SMO观测反电动势正弦度更高,观测位置与观测转速抖动更小;

(2)该观测器有一定的抗外部扰动能力,在负载扰动的情况下表现良好;

(3)观测器闭环运行效果较好,具有一定的实用应用价值。