刚性弹体带攻角斜侵彻贯穿混凝土靶板的理论模型

刘泓甫,黄风雷,白志玲,段卓平

(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)

0 引言

攻角的存在会显著改变弹体进入目标时的运动轨迹和姿态,因此受到人们的广泛关注。近年来科研工作者进行了大量带攻角侵彻实验[1-4],数据表明攻角的存在对弹体侵彻过程中的偏转及速度损失有显著的影响。吴普磊等[3]、朱战飞等[5]、路志超等[6]、Zheng等[7]、吴世永等[8]、马爱娥等[9]对弹体带攻角侵彻靶板时的运动状态使用有限元软件进行了数值模拟,并简要分析了攻角对侵彻深度(简称侵深)、偏转角的影响规律。在理论研究方面,国内外学者针对弹体侵彻半无限靶的过程建立了弹体平面运动模型,计算了有攻角情况下弹体的运动情况[10-13]。何翔等[10]将计算获得的侵彻行程、弹体轨迹等与实验数据进行了对比,并研究了初始状态改变对侵彻过程中轨迹及过载的影响;高旭东等[11]的计算结果表明,攻角的存在可以加剧或抑制侵彻过程中弹体的偏转,进而影响弹体侵深及水平方向位移;Chen等[12]分别给出了攻角和倾角对弹体侵深的影响系数,并得到了二者共同作用下的侵深预测公式;薛建峰等[13]在建立模型时加入了对靶体表面层裂机理的考虑,认为弹体的偏转主要发生在开坑阶段,并将计算结果与实验数据进行了对比。

在弹体侵彻贯穿有限厚混凝土靶的理论研究方面,Chen等[14]针对斜侵彻状态,提出了开坑、隧道和剪切冲塞3阶段模型,认为偏转发生在弹体开坑时,但其对侵彻薄靶的计算结果与大多数实验中弹体偏转趋势相反;针对此问题,段卓平等[15]和 Duan等[16]确定了3种不同厚度靶板的区分方法,认为对中厚度靶和薄靶,偏转不仅出现在开坑阶段还出现在冲塞阶段,且其偏转方向往往与初始偏转相反,并建立了姿态偏转理论模型,可用来计算弹体斜侵彻贯穿混凝土靶后的状态。但上述两种模型均未考虑攻角对弹体轨迹和姿态的影响,仅适用于计算无攻角的斜侵彻。

目前关于攻角对弹体侵彻贯穿有限厚混凝土靶的影响研究仍处于实验和数值模拟阶段,极大地制约了当前侵彻战斗部毁伤威力的快速评估。为了解决弹体带攻角斜侵彻贯穿混凝土靶板后弹体姿态和弹道快速预估难题,本文考虑开坑阶段弹头表面应力非对称分布及受力面积变化的影响,结合已有的姿态偏转理论模型[15-16],建立了刚性弹体带攻角斜侵彻贯穿混凝土靶板的理论模型。

1 刚性弹体带攻角斜侵彻贯穿混凝土靶板的理论模型

定义弹体接触靶板前的运动参量,如图1所示:v0为初速,α为攻角,ψ为初始姿态角,θ为倾角,有θ=ψ-α。攻角及姿态角的正负代表其方向;对于弹体侵彻中出现的偏转,若该偏转使姿态角变大,则其为正偏转,反之则为负偏转。

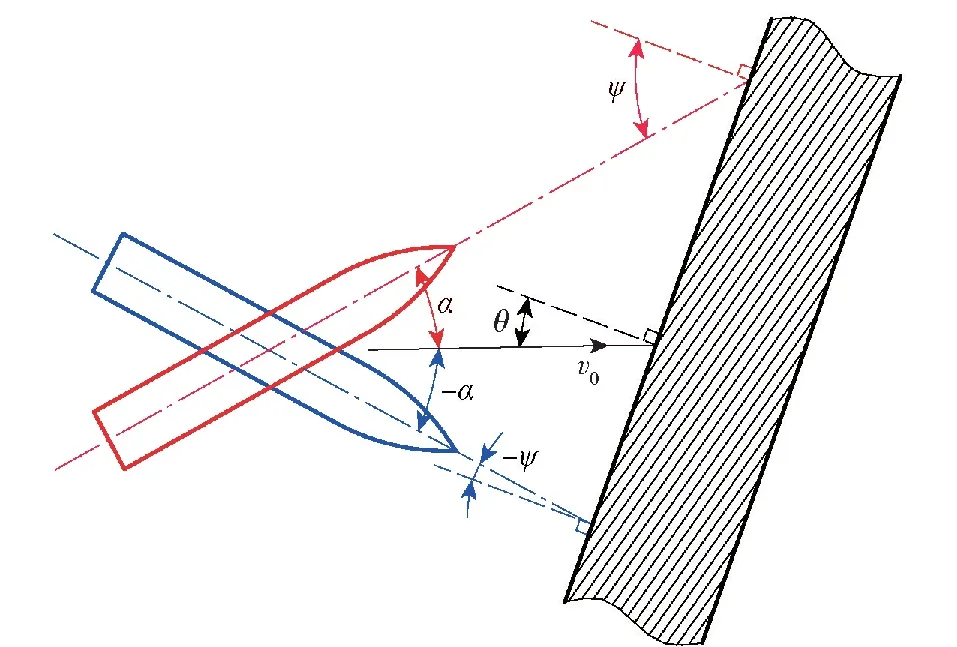
图1 弹体初始状态

如图2所示,弹体贯穿不同厚度靶板时将经历不同侵彻阶段,Δψ1、Δψ2分别为弹体开坑阶段偏转角和冲塞阶段的二次偏转角,H*为冲塞块厚度。靶板厚度的区分方法及对应的侵彻阶段可见文献[15-16],本文不再赘述。

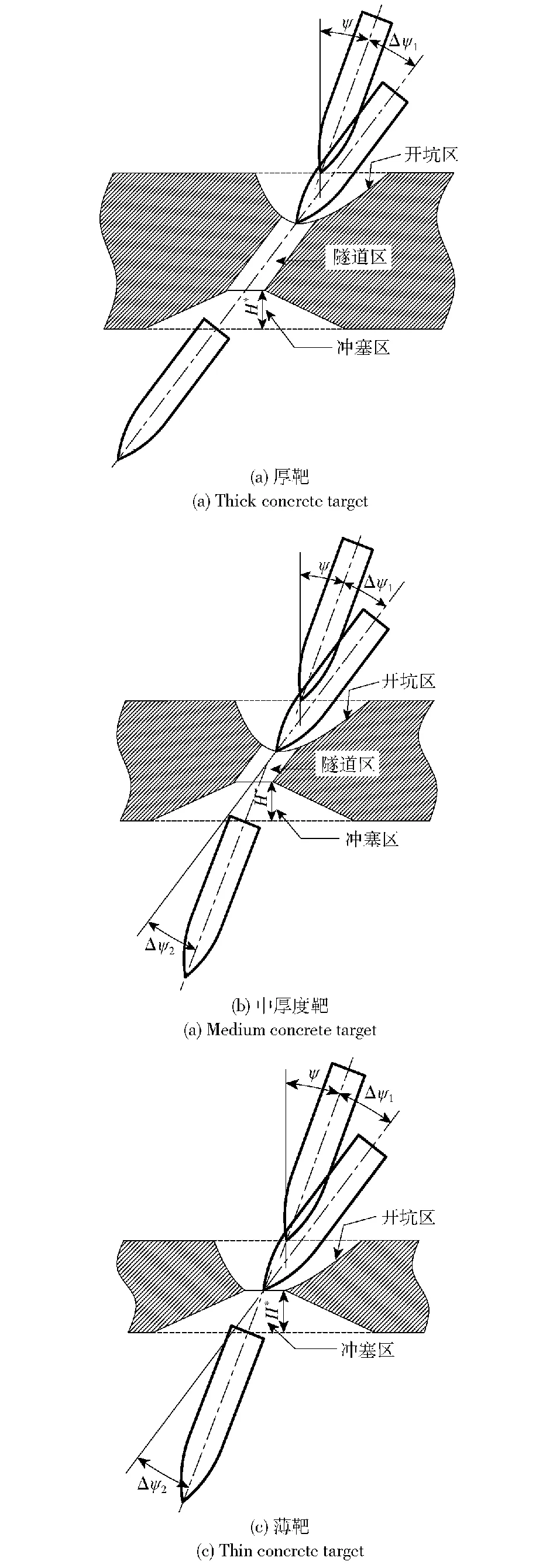
图2 弹体贯穿不同厚度混凝土靶

以尖卵形弹头的侵彻弹作为分析对象,在有攻角的条件下斜侵彻有限厚混凝土靶,如图3所示:弹径为d;弹头长度为lp,弹尖距质心C的距离为L,二者之差为ld;靶厚为H。为描述弹体在平面中的运动情况,建立全局坐标系O1xy,原点O1固定在弹体接触混凝土靶瞬时的质心位置,x轴为接触瞬时弹体轴线方向,y轴为平面内与x垂直的方向即弹体径向,O1xy面为弹道平面,质心在x轴上的位移同时表示了弹体侵深。

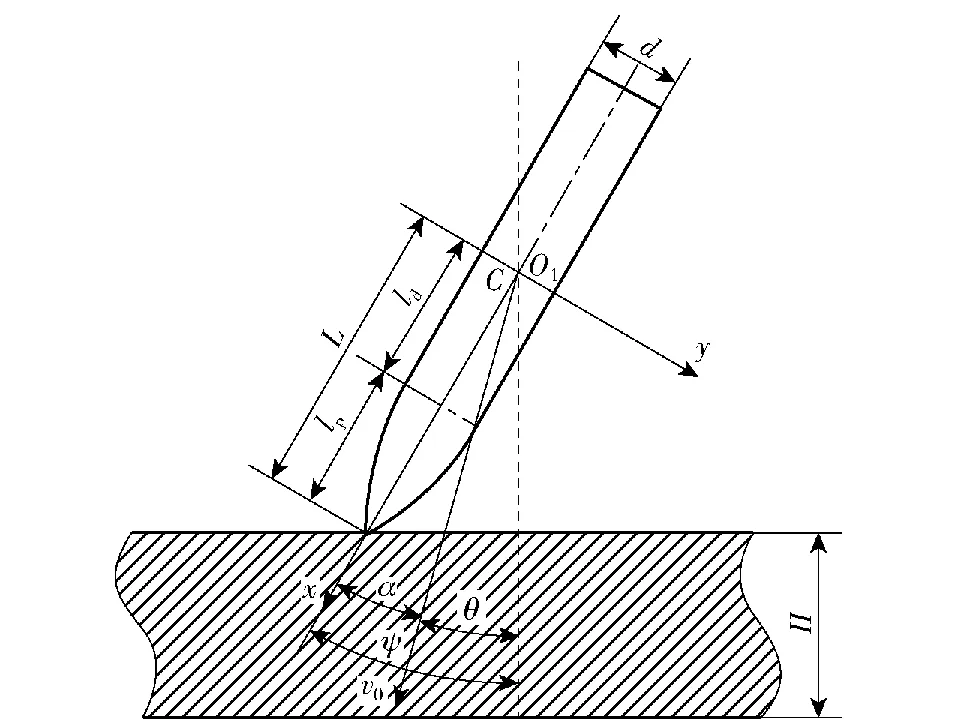
图3 尖卵形弹带攻角斜侵彻混凝土靶

在建立模型之前,提出以下假设:

1)弹体为刚体,不考虑变形和损伤。

2)弹体仅在弹头部分受到的阻力作用。

3)弹体运动过程中无绕弹轴的旋转,仅做平面运动。

4)忽略钢筋和骨料,认为混凝土为均质各向同性材料。

5)考虑到侵彻过程中弹体所受摩擦力作用很小,将其忽略。

1.1 弹头表面应力分析

表面应力法是确定斜侵彻过程中弹体受力的常用方法,由球形空腔膨胀理论可获得弹头表面法向应力[17]表达式:

(1)

计算目标点法向应力还需要求其法向速度。建立如图4所示的局部坐标系,原点O2在质心处,X为弹体轴向,Y为弹体径向,Z轴垂直于O2XY面向外。可以用坐标(X,φ)来描述弹头表面上的任一点,其中φ是Y轴负方向与该点所在横截圆面上半径的夹角,有X∈[ld,L],φ∈[0 rad, 2π rad]。

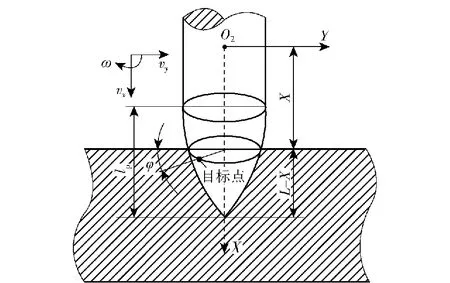
图4 弹体坐标示意图

设弹体质心的轴向和径向速度分别为vx、vy,角速度为ω,则弹头表面上任一点速度v可表示为

(2)

式中:ξ为目标点在O2XY面上投影点与质心的连线l跟X轴正向的夹角(见图5(a)),ξ=arctan(r/X),l=(X2+r2)1/2,r为投影点到目标点所处横截面圆心的距离,r=Rcosφ,R为目标点所处横截面半径,R=d/2+sy-s,sy=[s2-(X-ld)2]1/2,s为弹头表面的曲率半径,有cosβ=sy/s,β为目标点处表面法向量与弹体径向方向的夹角(见图5(b))。

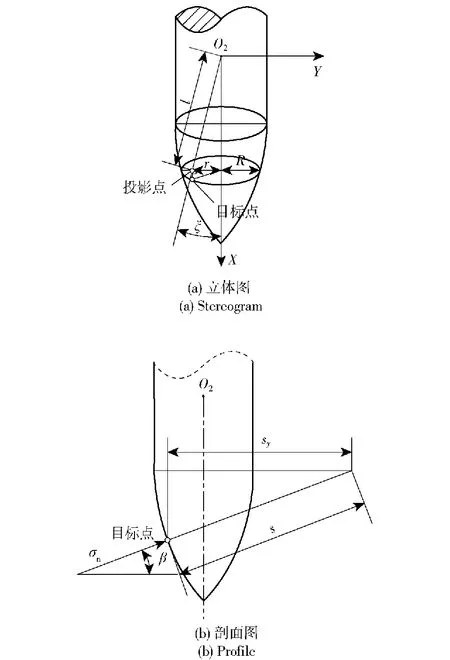
图5 弹头表面几何关系示意图

尖卵形弹头表面公式为

R2=Y2+Z2

(3)

则弹头表面任一点处的法向量可表示为

(4)

由式(2)、式(4)可求出该点的法向速度为

(5)

式(5)代入式(1),即可获得由质心速度及角速度表示的弹头表面任一点的法向应力σn。

取面积微元dA,有

(6)

用FX、FY、M分别表示弹体所受的轴向、径向阻力和偏转力矩,则微元上的受力可表示为

(7)

在不考虑开坑阶段自由表面效应及受力面积不同的影响下,对[ld,L]区间内的弹头表面应力进行积分,同时考虑表面应力关于侵彻平面分布的对称性,可获得弹头完全进入靶体后弹体所受的阻力及偏转力矩

(8)

(9)

(10)

弹体受力状态确定后,即可给出弹体侵彻过程中的运动微分方程:

(11)

式中:m和Jc分别为弹体质量和转动惯量。FX、FY、M的表达式由全局坐标系下的速度vx、vy、ω及弹靶参数构成,因其过于复杂,故不再详细写出。

1.2 弹体带攻角斜侵彻混凝土靶板的开坑阶段

在本文所讨论速度范围内,攻角对弹体运动的影响主要集中在开坑阶段,因为开坑阶段存在弹头进入过程及自由表面效应,不能直接由式(8)～式(11)简单求解弹体的运动状态,需要对此阶段内弹体的受力进行更详细的讨论,以建立弹体带攻角斜侵彻混凝土靶板的开坑模型。

针对不同厚度的混凝土靶板,开坑阶段分为完整开坑和不完整开坑。

1.2.1 完整开坑

如图2(a)、图2(b)所示,弹体在侵彻厚靶及中厚度靶时开坑阶段完整,开坑深度为kd,有k=0.707+lp/d[18]。弹体斜侵彻时,在开坑阶段将受到自由表面效应的影响,此外,完整开坑又分为弹头进入阶段和完全进入后的剩余开坑阶段两个小阶段,不同阶段受力区域不同,应该分开计算。

斜侵彻造成的自由表面效应采用文献[19-20]提出的衰减函数f(d*,a,vn)描述:

(12)

(13)

式中:a、b、d*分别表示空腔膨胀半径、混凝土塑性响应区外径、弹头表面微元沿外法线到自由面的距离与空腔膨胀半径a之和(见图6),d*可由几何关系直接获得,b=a(2E/3τ)1/3,E为混凝土弹性模量,τ为Mohr-Coulomb准则下的内聚力,有τ=(3-λ)fc/3,λ是压力硬化系数,对于混凝土,λ=0.67;γ=6/(3+2λ)。对于脆性材料,可认为塑料区由粉碎颗粒组成,当计算所得的塑性区域外径b大于弹轴到自由表面的距离d*时,混凝土对弹体无阻力,f(d*,a,vn)=0。

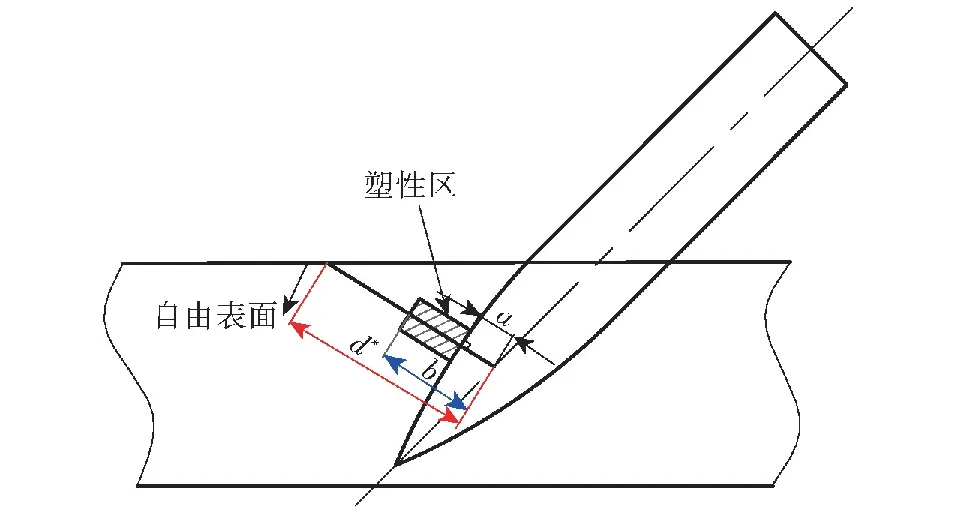
图6 自由表面效应示意图

因此,自由表面作用下的弹头表面正应力可表示为

σnf=f(d*,a,vn)σn

(14)

此外,开坑阶段包含弹头逐渐进入的过程,上下表面的受力区域不同且时刻发生变化,需要在计算中确定不同时刻弹头的受力区域。采用数值积分的方法,计算弹体在侵深为x时的轴向、径向阻力及偏转力矩,将所获阻力代入式(11),即可求解出弹体在开坑阶段的运动状态。弹头进入阶段的求解过程如图7所示。

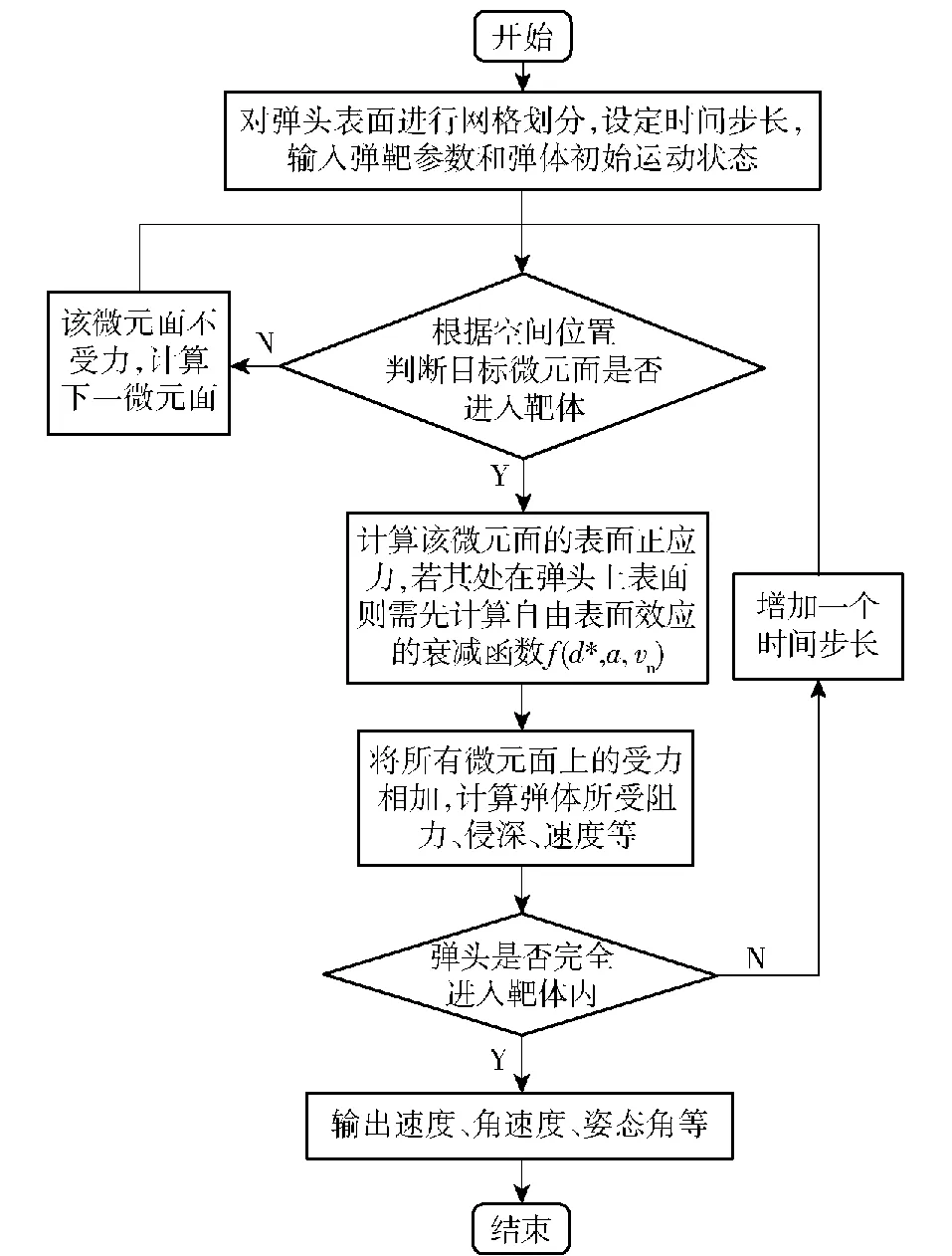
图7 弹头进入阶段计算过程

将图7中“判断目标微元面是否进入靶体”这一步移除,同时将获得的弹头完全进入时的运动状态作为弹体的初始运动状态,结束条件设置为“侵深是否到达kd”,即可获得对剩余开坑阶段的计算过程。

1.2.2 不完整开坑

不完整开坑发生在弹体侵彻薄靶时,如图2(c)所示,其开坑阶段的深度并不是kd,需重新计算。设冲塞块厚度为H*,则开坑深度为(H-H*)sec(ψ+Δψ1)。

姿态偏转理论模型[15-16]对开坑阶段进行了简化处理,认为开坑阶段的轴向阻力与侵深x呈正比,将开坑结束时的轴向阻力与冲塞块崩落临界力联立,由此求出了冲塞块厚度和开坑深度。但本文所建模型在开坑阶段的轴向阻力并不能仅用侵深x简单表示,不能求出开坑深度的解析解,只能使用计算程序获得其数值解,求解过程如图8所示。

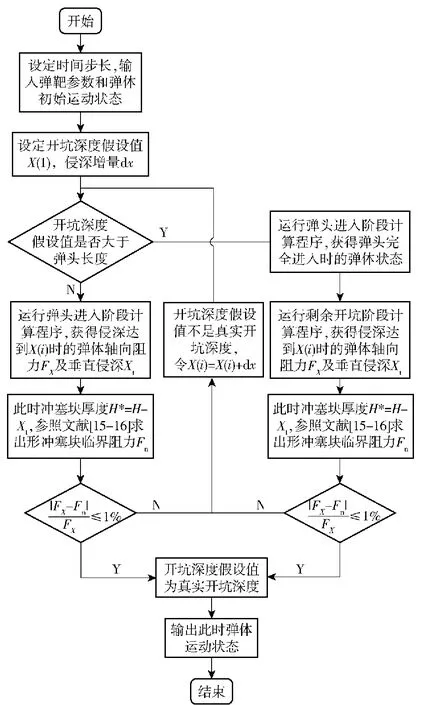
图8 不完整开坑阶段计算过程

1.3 隧道阶段和剪切冲塞阶段

通过1.1节和1.2节的讨论,建立了弹体带攻角斜侵彻混凝土靶板的开坑模型,可计算开坑结束时弹体的运动状态。根据不同的靶厚,后续将经历隧道阶段(厚靶/中厚度靶)和剪切冲塞阶段,不同靶厚的隧道及剪切冲塞阶段的计算参照文献[15-16],受限于篇幅,本文不再赘述。

2 模型验证

为验证本文所建立的理论模型,对不同侵彻实验进行计算(数据来自文献[1-2,21]及实验结果)。实验所用的弹靶参数及结果对比分别如表1、表2和表3所示。

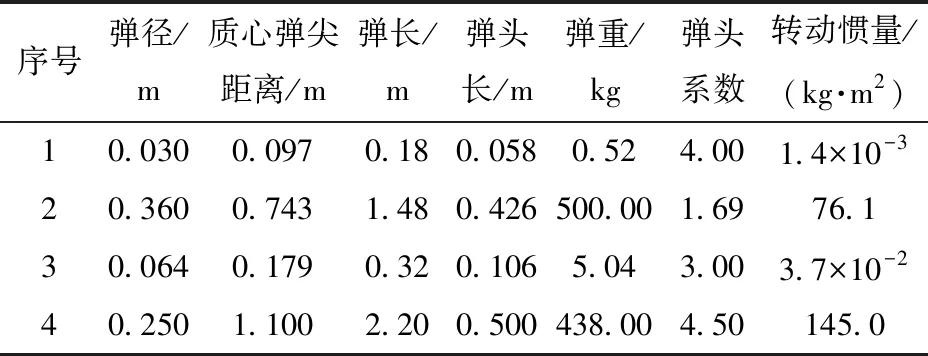
表1 弹体参数

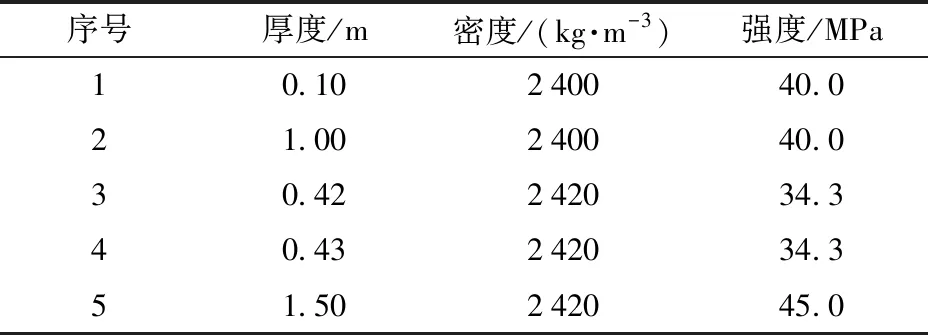
表2 靶体参数

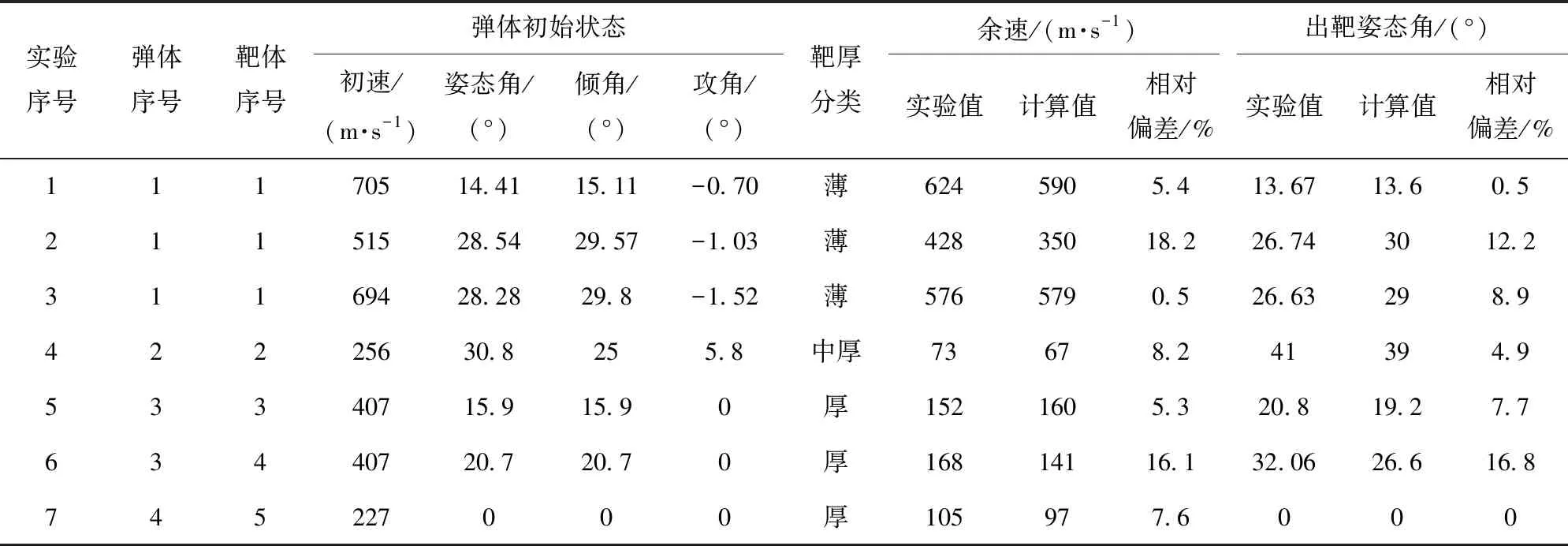
表3 计算结果与实验结果对比

针对上述不同弹靶参数及不同弹体初始状态下的侵彻实验,模型计算获得的余速及出靶姿态角跟实验结果的相对偏差均在20%以内,这表明本文带攻角理论模型将开坑阶段细分为两个阶段,严格判断不同时刻弹体受力区域,并使用衰减函数来表示自由表面效应的方法是合理的,可以较为准确地预测弹体带攻角贯穿靶板后的运动状态。

3 理论计算结果与分析

3.1 弹体开坑阶段受力

使用本文理论模型对表3中的实验4进行计算。倾角取值为10°,攻角取值分别为-4°、-2°、0°、2°、4°,其余参量不变,获得弹体开坑阶段的轴向阻力和径向阻力,结果如图9和图10所示。

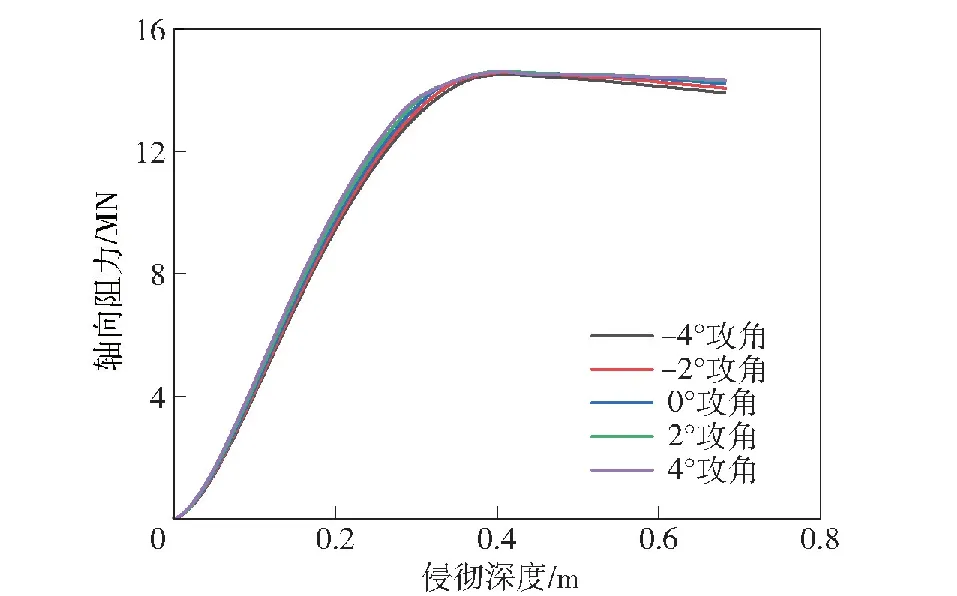
图9 轴向阻力

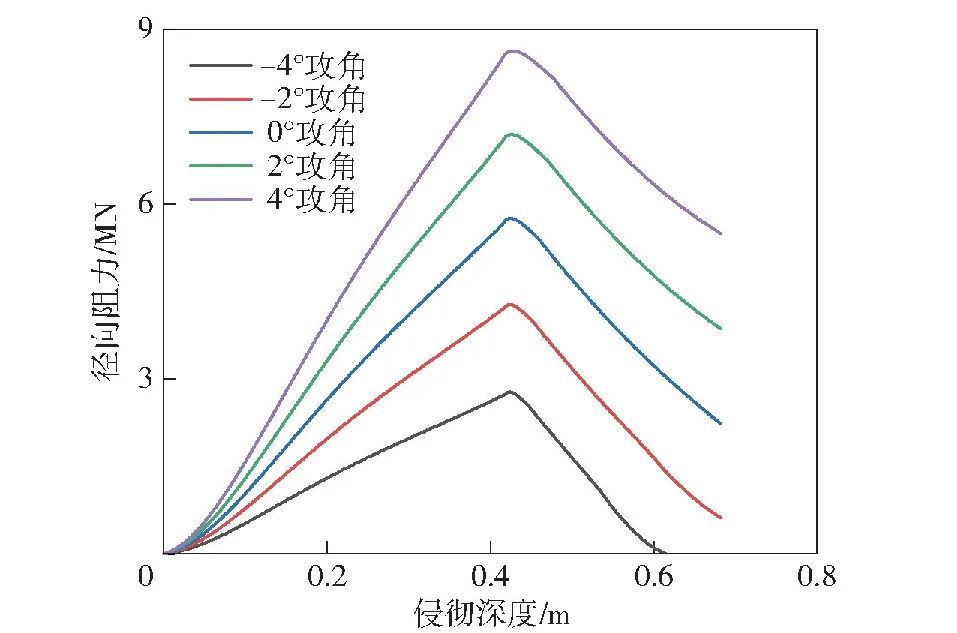
图10 径向阻力

从图9和图10可以看出:对轴向阻力,改变攻角其值无明显差异,说明轴向阻力受攻角的影响程度较小;对径向阻力,攻角越大,阻力值越大,且随着攻角的变化,径向阻力变化明显,说明其受攻角的影响程度较大。

轴向阻力和径向阻力内的变化均分为两个阶段。对轴向阻力,第1阶段阻力随侵深逐步上升,直到弹头完全进入靶体;在第2阶段,阻力基本不变。对径向阻力,第1阶段阻力随侵深逐步上升,在弹头完全进入靶体时达到最大;第2阶段则随着侵深的增加而逐渐下降。

分析两种阻力呈现图示变化趋势的原因:侵彻时随着弹头进入靶体,受力面积显著增加从而导致弹体所受阻力变大,弹头完全进入靶体时受力面积达到最大,故在弹头完全进入前,两阻力会持续上升;弹头完全进入后,随着侵彻的进行,弹体轴向速度变化较小,径向速度逐渐降低,且自由表面效应显著减弱,弹头受力分布逐渐对称,因此轴向阻力基本不变,而径向阻力则逐渐下降。

3.2 弹体出靶余速和姿态角

采用本文所建立的理论模型,计算不同攻角下弹体分别以10°、20°、30°倾角斜侵彻混凝土中厚度靶的情况,所用弹靶参数采用实验4中的型号,弹体初速为300 m/s,攻角取值为-10°～10°,计算间隔为2°。余速和姿态偏转角的计算结果分别如图11和图12所示。

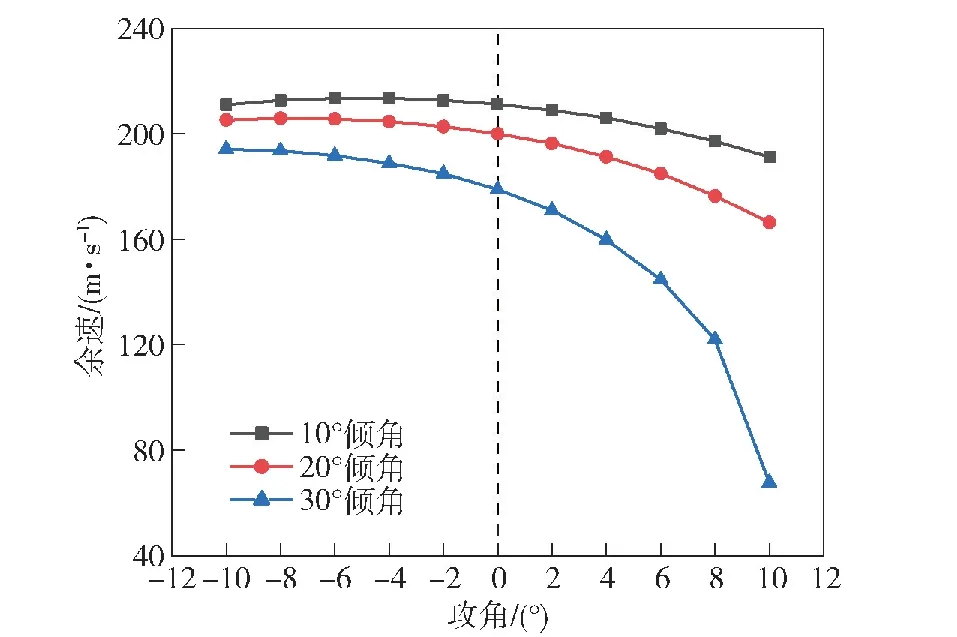
图11 攻角对余速的影响

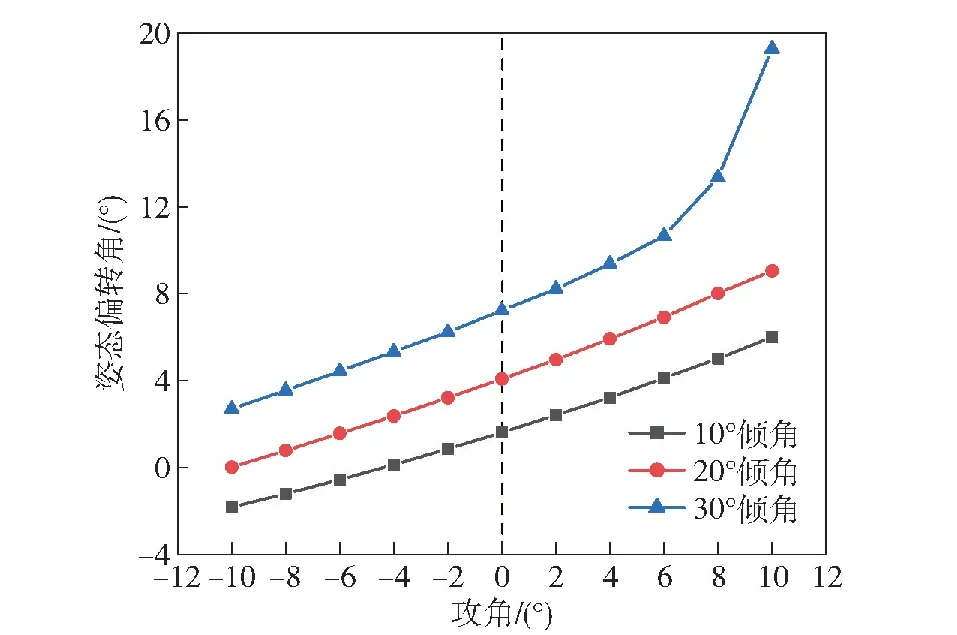
图12 攻角对姿态偏转角的影响

由图11可以看出,在一定倾角条件下,正攻角会降低弹体的余速,而适当的负攻角可提高弹体的余速,当负攻角与倾角的绝对值比值为1/3时,弹体余速接近最大。此外,倾角越大,余速越容易受到攻角变化的影响,如30°倾角下的余速曲线,在攻角值从-10°到10°的变化过程中,其余速变化量为 126 m/s,而其余两种倾角下余速变化量仅为20 m/s和39 m/s。

由图12可以看出,在一定倾角条件下,正攻角会加剧弹体偏转,而负攻角会抑制弹体偏转。对倾角较小的斜侵彻,姿态偏转角与攻角近似成线性关系;当倾角较大(30°)时,攻角的值超过一定范围后,姿态偏转角更容易受到攻角改变的影响,攻角增加,姿态偏转角会急剧上升,其原因是随着攻角的增加,上下表面受力面积不对称程度加剧,上表面自由表面效应也更加显著,二者同时作用导致弹体在开坑阶段内的偏转急剧增加。

弹体贯穿薄靶/中厚度靶时,开坑和冲塞阶段会经历两次偏转,图13和图14分别是不同倾角条件下攻角对开坑阶段偏转角和冲塞阶段的二次偏转角的影响规律。

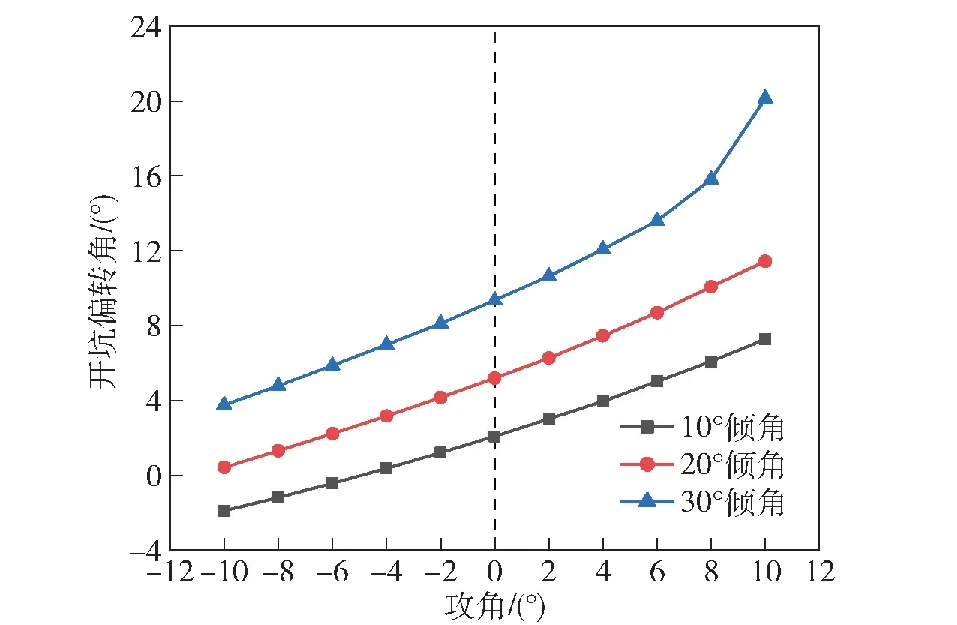
图13 攻角对开坑阶段偏转角的影响

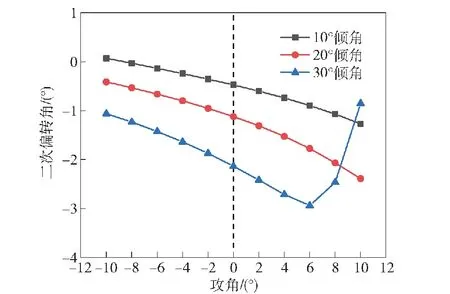
图14 攻角对二次偏转角的影响

如图13所示,正攻角会加剧弹体在开坑阶段的偏转,而负攻角可以抑制开坑阶段的偏转。对倾角较小的斜侵彻,开坑阶段偏转角与攻角近似成线性关系;当倾角较大(30°)时,攻角的值超过一定范围后,如前文所分析,开坑阶段偏转角急剧上升。

根据图14可以看出,倾角较小时,二次偏转角与攻角近似呈线性关系,正攻角加剧二次偏转,而负攻角抑制二次偏转。倾角较大(30°)时,攻角的值超过一定范围后,弹体的二次偏转角迅速减小,其原因是二次偏转角的大小是由冲塞阶段开始时姿态角、弹体轴向速度、隧道区长度等共同决定的,随着攻角的增加,隧道区域不断变长,且弹体轴向速度不断降低,同时作用下,当攻角到达某一临界值时,弹体的二次偏转角迅速减小。对于二次偏转需要指出的是,攻角对其的影响是通过对开坑阶段弹体运动的影响间接作用的。

4 结论

本文建立了刚性弹体带攻角斜侵彻贯穿混凝土靶板的理论模型,对不同工况下的侵彻实验进行了计算,并讨论了不同倾角条件下攻角对弹体余速和偏转的影响规律。得出以下主要结论:

1)使用本文模型对不同侵彻实验进行计算,与实验相比误差均在20%以内,说明模型能够实现对弹体带攻角斜侵彻贯穿混凝土靶板弹道和弹体姿态的快速预估。

2)攻角增大会使弹体开坑阶段内所受径向阻力变大,偏转力矩上升,弹体受力情况更加恶劣,理论模型的计算结果可为弹体设计提供依据。

3)在一定倾角条件下,正攻角会加剧弹体偏转并降低弹体的侵彻能力,负攻角会抑制弹体偏转且适当的负攻角能提高弹体的侵彻能力;倾角越大,侵彻能力和偏转角越容易受攻角改变的影响。