多飞行器协同任务分配的改进粒子群优化算法

2023-09-07王磊徐超李淼赵慧武

兵工学报 2023年8期

王磊, 徐超, 李淼, 赵慧武

(1.北京特种机电控制研究所, 北京 100012; 2.北方自动控制技术研究所, 山西太原 030051)

0 引言

在当今军用和民用领域,飞行器在目标搜索、对地攻击、空中搜救、交通巡查以及快递运输等方面发挥着重要作用[1]。因为单架飞行器无法高效率的完成复杂任务,经常需要使用多个飞行器协同完成复杂任务。因此,多飞行器系统在复杂的任务环境实现灵活的任务,已成为重要研究内容[2],多飞行器协同任务分配问题已成为飞行器自主导航领域亟需解决的关键问题[3]。

多飞行器协同任务分配是指:给定飞行器的种类及数量,根据一定的物理环境信息和任务要求,将一个或多个任务分配给一个飞行器,当所有飞行器完成所分配的任务后,整个飞行器编队的整体效能达到最优[4]。在解决多飞行器任务分配问题时,需考虑飞行器的任务能力上限、任务时序约束以及实时规划有效性等要求[5]。理论上,多飞行器任务分配问题属于非确定性多项式困难(NP-hard)的排列组合问题。对于大规模系统,难以完全避免组合爆炸问题。目前,研究者提出了多种计算可行的协同任务分配算法。文献[6]提出一种基于“招标-投标-中标”的市场拍卖机制,设计了多Agent分布式任务分配算法。文献[7]重点研究了实际任务环境中存在的不确定性约束条件,提出一种分布式多无人机协同任务分配方法。文献[8]提出了基于拍卖和一致性原理的分布式任务分配算法。文献[9]利用混合整数规划的方法研究了无人机搜索任务分配问题,给出问题的最优解。智能进化算法因为具有灵活、易实现和计算复杂度低的特点,被广泛地用于多飞行器协同任务分配的研究。文献[10]在多子群蚁群算法的基础上,提出了基于分工机制的蚁群算法求解无人机协作多任务分配问题。文献[11]建立了蝗虫仿生算法用于多无人机搜救任务。文献[12]提出一种改进遗传算法(GA),用于集中式在动态环境中给无人机任务分配任务。文献[13]将差分进化算法用于解决任务分配问题。文献[14]提出基于和声搜索算法的任务分配算法。

与其他智能进化算法相比,粒子群优化(PSO)算法具有较强的寻优能力,且鲁棒性较强。文献[15]提出用于调整PSO算法的主要控制参数的自适应策略,并研究了PSO算法的收敛性。为了进一步提高PSO算法在解决任务分配问题的效率,文献[16]采用混合整数规划的方法构造适应度函数。文献[17-20]提出了多种用于任务分配和路径规划的改进PSO(MPSO)算法。

本文研究了多飞行器协同任务分配问题,提出了一种任务分配MPSO算法。主要创新点包括:基于粒子连续性的位置和速度,解码出离散化的任务分配方案,即实现了PSO算法连续性解的离散化;为了防止算法过早陷入局部收敛的问题,根据模拟退火算法原理,建立一种跳出局部收敛的策略,并将这种策略嵌入到PSO算法的每一次迭代中;与其他算法进行了对比实验,验证了本文提出的MPSO算法的有效性。

1 多飞行器协同任务分配数学模型

本文基于水平二维战场环境研究了多飞行器协同任务分配问题。每架飞行器按照一定的攻击顺序对地面多个目标进行打击,同时目标也能侦查、攻击飞行器,对飞行器具有一定的防空威胁。

假定总共有Nu架飞行器U={U1,…,UNu}和Nt个目标T={T1,…,UNt},需要对每个目标执行一次攻击任务,因此相应的共有Nt个任务M={M1,…,MNt}。飞行器数目远远小于任务数目,即Nu≪Nt。本文研究的任务分配问题的目标是为每架飞行器Ui指派一个顺序攻击任务集合Θi:

Θi=〈Mw,1,Mw,2,…,Mw,k〉

(1)

式中:Θi为给飞行器Ui指派的任务,所有任务Θi就构成了一个任务分配解或方案,i∈{1,…,Nu}。当Ui执行Θi时,先从初始位置Bi起飞,先执行任务Mw,1, 然后攻击Mw,2,以此类推,依次攻击Θi中的任务。Ui攻击完最后一个任务Mw,k后返回初始位置Bi,总航程表示为dis(Θi)=dis(Bi,Tw,1)+Σs∈{1,…, k-1}dis(Tw,s,Tw,s+1)+dis(Tw,k,Bi),其中函数dis(·)表示两个任务的相应目标或初始位置与目标之间的距离。如图1描述了飞行器U1、U2以及 5个任务M1～M5的位置坐标,同时也表示将任务M1、M2和M4依次分配给了U1,将M3和M5分配给了U2,即一组任务分配解Θ1=〈M1,M2,M4〉以及Θ1=〈M3,M5〉。

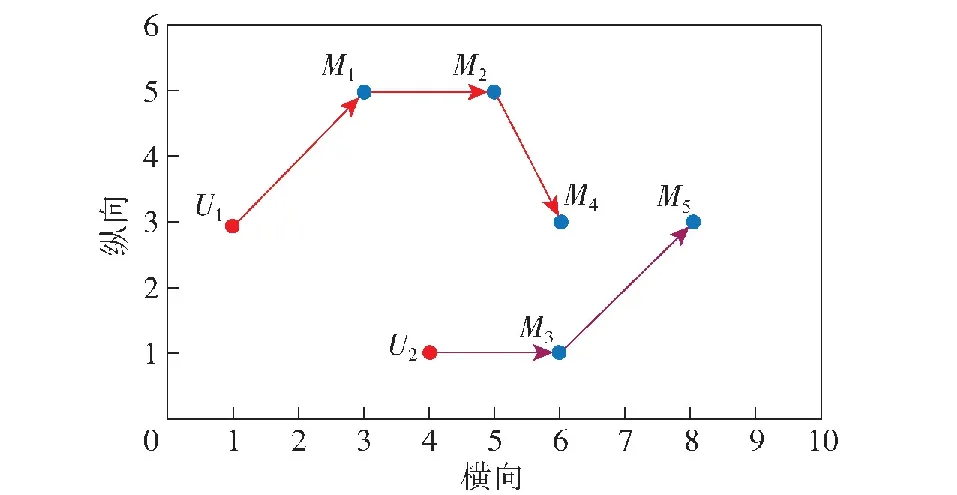
图1 多飞行器协同任务分配示意图

利用0-1变量xij表示飞行器Ui执行任务Θi时是否执行第j个任务Mj:

(2)

通过为飞行器合理分配攻击目标,保证飞行器编队整体作战性能最好。实际上,多飞行器协同任务分配是个排列组合优化问题,需要考虑以下的约束、代价与收益:

(3)

每个目标只能指派给一个飞行器,不能重复分配。此约束表示为

(4)

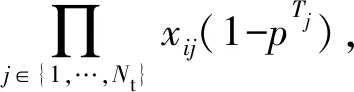
(5)

3)航程代价。飞行器需要飞行一定航程完成任务。通过将航程代价指标最小化,尽可能地减少资源消耗。飞行器Ui执行任务Θi的航程代价函数为

minLi=dis(Θi)

(6)

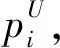
(7)

综合上述分析,可得飞行器协同任务分配问题的数学模型为

(8)

s.t.式(3)和式(4)

xij∈{0,1},∀i∈{1,2,…,Nu},∀j∈{1,2,…,Nt}

式中:s1、s2和s3分别是威胁代价、航程代价以及攻击收益对应的权重。类似文献[15]的分析,本文均衡考虑威胁代价、航程代价和攻击收益,因此设定s1=1、s2=1、s3=1。

2 基于MPSO算法的多飞行器协同任务分配方法

2.1 PSO算法原理

PSO算法中,一定数目的粒子组成种群,每个粒子代表问题的一个潜在解。每个粒子有两个属性:位置和速度。在种群进化过程中,粒子需要追踪两个极值:一个是粒子自身历史的最优解,称为个体极值;另一个是整个种群当前的最优解,称之为全局极值。所有粒子基于这两个极值更新位置和速度,从而尽快向最优解靠拢。如果问题的解是D维的,那么相应粒子的位置和速度都可看做D维向量。假设粒子Pk在t时刻的位置和速度分别是Yk,t=(Yk,t[1],…,Yk,t[D])和Zk,t=(Zk,t[1], …,Zk,t[D]),它们按照式(9)和式(10)演化:

Zk,t+1[j]=w·Zk,t(t)[j]+c1·Rand1·(pbestk,t[j]-Yk,t[j])+c2·Rand2·(gbestk,t[j]-Yk,t[j])

(9)

Yk,t+1[j]=Yk,t[j]+Zk,t[j]

(10)

式中:w称为惯性权重,根据文献[15]分析,通常情况下令w=0.721 3;c1和c2是自然常数,通常情况下令c1=c2=2;Rand1和Rand2是分布在[0, 1]之间的随机数;pbestk,t是粒子Pk当前时刻t的个体极值;gbestk,t是种群当前找到的全局极值。在种群进化过程中,粒子Pk的任一位置分量Yk[j]被限制在最大位置Ymax和最小位置-Ymax之间,如式(11)所示:

(11)

传统PSO算法流程如下:

1)设置粒子种群规模、最大迭代次数,初始化粒子位置和速度,计算每个粒子的个体极值和全局极值。

2)计算每个粒子的适应度函数值,如果该值优于该粒子当前个体极值,则更新该个体极值;如果某个体极值优于当前的全局极值,则更新全局极值。

3)按照式(9)和式(10)更新每个粒子的位置和速度。

4)如果迭代次数达到最大迭代次数,则停止迭代,输出全局极值为当前最优解,否则,转入步骤2。

2.2 用于多飞行器协同任务分配的MPSO算法

利用PSO算法解决多飞行器协同任务分配问题,需要解决以下两个难点:1)任务分配问题属于排列组合优化问题,其解空间是离散的,而传统PSO算法只能给出连续性的解。因此,需要建立PSO连续性的解与离散化的任务分配方案之间的一一对应关系,即离散化PSO算法的解;2)PSO算法具有操作简单、容易收敛的优点,但也容易过早陷入局部收敛。为解决上述两个问题,本文将粒子的位置编码为一组任务分配向量,然后将分配向量解码为一组任务分配方案,实现了PSO算法连续性解的离散化。同时,基于模拟退火算法原理,本文提出一种跳出局部收敛的策略,根据策略运用生成新粒子,解决了局部收敛问题。

2.2.1 编码与解码

令粒子的位置和速度都是Nt维向量,即D=Nt,那么解空间也是Nt维。令粒子的位置上限等于飞行器的数目,即Ymax=Nu;令函数K(z)表示不大于z的最大整数,例如K(2.3)=2。

为了更好地解决任务分配问题,将粒子Pk的位置Yk编码为一列分配向量Ak=(Ak[1],Ak[2],…,Ak[Nt]),

(12)

很明显,因为Yk[j]∈[-Nu,Nu],可知Ak[j]是整数且Ak[j]∈[1,Nu]。

算例1考虑一个多飞行器协同任务分配问题,其中Nu=3,Nt=14,即将14个不同目标T1～T14分配给飞行器U1～U3。很明显,其解空间是14维。将粒子Pk的位置和速度都限制在[-3, 3]之间,则相应的一组的位置和速度如表1所示。根据式(12)可得Pk对应的任务分配向量Ak,同样如表1所示。

表1 一个粒子的位置、速度和相应的分配向量

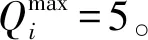
算法1:

输入:分配向量Ak

输出:任务分配方案Θi,i∈{1,…,Nu};

1 for (iinNu){

2 for (jinNt){

3 if (Ak[j]=i){

4Ψ(i)=Ψ(i) ∪ {Tj};

5 }

6 }

7Start[i]=Bi,Θi=∅,TN[i]=0; ∥初始化

8 }

9Ψ=∅;

10 for (iinNu){

11 while (Ψ(i)≠∅){

12 选择Ts∈Ψ(i);

14Start[i]=Ts;

15TN[i]=TN[i] + 1;

16Ψ(i)=Ψ(i) {Ts};

17 将Ts添加到顺序集合Θi的末尾;

18 }

19 else{∥当前给Ui分配目标超过其上限

20Ψ=Ψ∪Ψ(i);

21Ψ(i)=∅;

22 }

23 }

24 } ∥初步分配

25 while (Ψ≠∅){

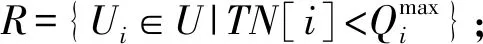
27 选择Ts∈Ψ;

28 选择Um∈K;

29TN[m]=TN[m] + 1;

30Start[m]=Ts;

31Ψ=Ψ {Ts};

32 将Ts添加到顺序集合Θm的末尾;

33 } ∥再次分配

34 输出Θi,i∈{1,…,Nu};

算法1的数组Start和TN都是Nu维的,其中,分量Start[i]表示当前时刻分配给飞行器Ui的末尾目标,分量TN[i]表示当前时刻分配给飞行器Ui的目标个数。集合Ψ表示受限于飞行器攻击能力约束、未能分配的目标集合。算法1可分为以下3个步骤:

1) (1～9行):根据分配向量Ak为每个飞行器Ui分配一组目标集合Ψ(i)。此时,Ψ(i)中目标的个数可能超过了Ui的攻击能力上限,并且也没有确定攻击目标的顺序。同时,初始化Start、Θi和TN,使得∀i∈{1,…,Nu},Start[i]=Bi,Θi=∅,TN[i]=0。

在初步分配过程中,对于U1,因为T9∈Ψ(1),将T9加入Θ1;接下来,Ψ(1)中剩余目标T10,将T10加入Θ1的末尾,依次类推,可得Θ1=〈T9,T10,T14,T12,T11〉,其数量达到了U1的任务能力上限,但此时Ψ(1)中还剩余一个未分配的目标T13,需要将T13并入Ψ,即Ψ={T13}。同理,可得Θ2=〈T1,T2,T3,T8,T4,〉,达到了U2的攻击能力上限,但Ψ(2)中目标T7未分配,只能将T7并入Ψ,此时Ψ=Ψ∪ {T7}={T13,T7}。类似的可得Θ3=〈T5,T6〉。

在再次分配过程中,只有U3没有达到攻击能力上限。因此,需要将Ψ={T13,T7}中的目标分配给U3。先把T13分配给U3,再把T7分配给U3,即把T13和T7依次添加到Θ3的末尾,可得Θ3=〈T5,T6,T13,T7〉。

因为PSO算法是从初始种群开始进化,初始粒子的质量会影响算法的收敛速度。为了使得初始种群中粒子分布的更加均匀,本文令例子Pk的位置Yk的每个分量Yk[j]满足[-Nu,Nu]之间的均匀分布,同理令Pk的初始速度向量Zk[j]也满足[-Nu,Nu]的均匀分布。

2.2.2 基于模拟退火算法的跳出局部收敛的策略

传统PSO算法很容易陷入局部收敛。受到模拟退火算法的启发,提出一种使得PSO算法尽快跳出局部收敛、扩大搜寻范围的方法。这种方法先以某种规则生成新粒子,然后按照概率函数判断是否接受这个粒子的更新。

1)局部搜索启动准则:为了平衡算法的对于解空间的开发和探索的能力,使用概率hk启动粒子Pk的基于模拟退火算法的局部搜索过程,hk由式(13)计算:

hk=1-0.01×102g/max_g

(13)

式中:g是当前迭代代数;max_g是最大迭代次数。即对于每个粒子Pk,产生一个随机数r∈[0,1]。如果r

图2 新粒子位置向量交叉与替换

算法2：

输入:粒子Pk、个体极值对应的粒子Pbestk和全局极值对应粒子Pgbest;

输出:新粒子Pk;

1 计算F(Pk)和F(Pgbest);

2 if (Ω1=F(Pk)-F(Pgbest)>0){

5 if (Ω>0){

6r=random[0, 1];

7 if (r≤exp[-Ω1×Ω])

9 else{

11 }

12 }

13 输出:粒子Pk;

2.2.3 飞行器任务分配问题的MPSO算法

本文提出了一种用于多飞行器协同任务分配的MPSO算法。首先,限定了粒子的位置大小,根据式(12)将粒子的位置编码为一组分配向量。然后,将得到的分配向量作为算法1的输入,解码得到一组满足约束式(3)的任务分配方案。在PSO算法更新进化过程中,每个粒子按照式(8)和式(9)来调整自己的速度和位置。选择合适的适应度函数,尽可能地减少飞行器付出的威胁代价和航程代价,提高飞行器编队的总体攻击收益。同时,提出的新粒子生成策略利用了模拟退火算法的思路,保留了全局极值的有效片段,以一定概率决定是否保留生成的新粒子,有效缓解PSO算法容易陷入局部收敛的问题。

MPSO算法流程如下:

1)初始化种群中的粒子的速度和位置,设置迭代次数max_gen,令g=0。计算全局极值和每个粒子的个体极值。

2)对每个粒子Pk执行如下的操作:

①执行算法2更新粒子Pk;

②根据式(12)将Pk的位置编码为分配向量Ak;

③执行算法1,将Ak解码任务分配方案Θi,i∈{1,…,Nu};

④根据得到的任务分配方案,计算适应度函数F(Pk);

⑤更新每个粒子的个体极值和全局极值;

3)根据式(8)和式(9)更新每个粒子的速度和位置,令g=g+1。

4)判断迭代是否结束,若g

5)输出全局极值及对应的任务分配方案。

3 实例仿真

算例3任务区域有15个目标T1～T15,3架飞行器U1～U3。目标和飞行器的位置、价值、威胁等属性都是随机产生,如表2和表3所示。本文分别用3种PSO算法(MPSO算法、PSO算法、PSO1算法)和一种GA求解此问题,并对比分析实验结果。验证平台是基于2.3 GHz的Core i9 9880H的MacBook Pro计算机,使用Python编写程序。其中,MSPO算法是由本文给出的算法;PSO算法利用了本文提出的算法1对粒子进行编码与解码,但没有试图解决局部收敛问题;PSO1算法由文献[15]给出,粒子的更新过程中没有修复粒子对应的解,保留了不满足要求约束条件的解;GA由文献[4]给出。

表2 目标情况

利用MPSO算法、PSO算法、PSO1算法和GA分别求解此任务分配问题。分别运行10次程序,并记录平均适应度值以及最优适应度值,图3给出了运行过程中各个算法的最优适应度值变化过程。得得到的各个算法最优解如表4所示。平均适应度值和最优适应度值如表5所示。从表5中可以看到,MPSO算法给出了最优结果562.85,PSO算法给出次优结果567.44,PSO1算法和GA给出的结果分别是574.55和563.08。很明显,MPSO算法要比其余3种算法性能更好。

表4 不同算法得到的最优分配解

图3 系统程序运行适应度值变化

因此,无论从最优适应度还是平均适应度来看,MSPO算法都给出了最好结果。

本文提出的MPSO算法在解码粒子时修正了对应的任务分配解,使之满足约束条件,并且引进了基于模拟退火算法的跳出局部收敛策略。分析可知:1)MPSO算法在更新粒子时,接受性能好的粒子,以一定概率接受性能较差粒子,而PSO算法不会接受性能较差的粒子。因此,在迭代初期,PSO算法表现要优于MPSO算法,但是到算法迭代后期,随着接受较差粒子的概率降低,MPSO算法体现出跳出局部极值的优点,这与图3中结果相一致;2)PSO1算法在更新粒子时没有修正对应的解,保留了不可行解,因此与MPSO算法和PSO算法相比,PSO1算法的性能较差,这也在图3中得到了体现;3)GA没有修正解码后的解,只保留可行解,因此收敛速度较慢、性能较差。