导弹突防概率解析与仿真计算结果差异分析
2018-10-29胡振震王亮杨宝庆胡玉理杨文
胡振震,王亮,杨宝庆,胡玉理,杨文
(中国洛阳电子装备试验中心,河南 洛阳 471000)
0 引言
弹道导弹突防概率计算[1-3]主要有2种方法: 一是解析计算;二是仿真计算。解析计算主要基于概率论等构建导弹突防概率解析计算表达式[4-9]。仿真计算通常利用蒙特卡罗方法构建突防仿真模型[10-13]。一般情况下2种方法得到的计算结果是一致的,但一些情况特别是攻击弹头略饱和(拦截弹数量略不足) 时,两者会存在明显的差异。
考虑一个简单的算例(a): 真实攻击弹头数w=10,重诱饵数α=0,轻诱饵数β=0,弹头可靠性PR=1.0,发现概率PD=0.9,跟踪概率PT=1.0,识别概率PI=1.0,拦截弹数量N=9,1枚弹头需求拦截弹数n=1,拦截弹可靠性Pr=1.0。分析这些数据很容易得到解析计算结果,拦截概率为1,拦截弹可靠性为1,弹头的跟踪识别概率都为1,弹头的可靠性为1,那么弹头都可靠且发现1枚就能拦截1枚,因为发现概率是0.9,那么能够发现9枚同时也能拦截9枚,即突防弹头是1枚,突防概率是0.1,然而仿真计算结果为突防弹头数1.349,突防概率为0.135。这2种方法哪一种是正确的,实际应用时应该采用哪一种方法的结果作为参考,这是决策者很关心的问题,也是本文需要解决的问题。
1 各阶段统一的解析和仿真计算模型
弹道导弹突破反导系统[14]的各个阶段(初、中、末段)可以用统一模型进行计算,各阶段的差异仅在于输入参数的不同(比如:弹头和诱饵是否分离,拦截策略等)。反导系统各阶段都可分预警和拦截[15]过程,预警过程主要有发现、跟踪、识别环节,计算需考虑发现概率、跟踪概率、识别概率,而拦截过程主要有拦截环节,需考虑拦截(或毁伤)概率。对于某一阶段的突防过程,假设有w个真实弹头和α个重诱饵,β个轻诱饵,弹头可靠性为PR,拦截弹的数量为N,可靠性为Pr。真实弹头的发现、跟踪、识别、拦截概率分别为PDw,PTw,PIw,PKw。重诱饵的发现、跟踪、识别、拦截概率分别为PDα,PTα,PIα,PKα。轻诱饵的发现、跟踪、识别、拦截概率分别为PDβ,PTβ,PIβ,PKβ。
1.1 解析计算模型
突防过程首先考虑发现和跟踪环节,则弹头和诱饵被发现和跟踪的数量为
wPRPDwPTw+αPRPDαPTα+βPRPDβPTβ.
考虑识别环节,弹头被识别为真弹头的概率为PIw,重/轻诱饵识别为弹头的概率PIα,PIβ,则弹头和诱饵识别为真弹头的总数(即需拦截的总弹头数)为
A=Aw+Aα+Aβ=wPRPDwPTwPIw+
αPRPDαPTαPIα+βPRPDβPTβPIβ.
考虑拦截环节,采用n拦1策略(即n枚拦截弹拦截1枚弹头,n枚拦截弹拦截1枚弹头的过程视为泊松流过程)。当nA≤N时,即拦截弹数量能满足n拦1的需求,被拦截的弹头和诱饵数量为
Aw[1-(1-PrPKw)n]+Aα[1-(1-PrPKα)n]+
Aβ[1-(1-PrPKβ)n].
当nA>N时,即拦截弹数量不足时,被拦截的弹头和诱饵数量为

因为考虑到诱饵和真实弹头都已被识别为真实弹头,不分彼此,所以拦截弹N/n对于弹头和诱饵来说是平均分配的,不考虑弹头和诱饵的不同导向概率[16],其比率为Aw∶Aα∶Aβ。因此,当nA≤N时,突防的真实弹头数为
wPR{1-PDwPTwPIw[1-(1-PrPKw)n]}.
当nA>N时,突防的真实弹头数为

总结起来,n拦1策略导弹突防概率的解析计算模型为
(1)
1.2 蒙特卡罗仿真模型
利用蒙特卡罗方法进行仿真实验,突防的弹头数量是最终的样本期望,样本则是一次突防实验的结果。样本值认为是一些随机变量的函数,这些随机变量则是定义在多个不同的事件空间上的实函数,具有某一概率密度[17]。直接影响突防弹头数量的事件包括弹头可靠性事件和弹头被拦截事件,而被拦截事件又与发现事件/跟踪事件/识别事件相关,还与拦截方的拦截弹数量和拦截策略有关,也与拦截的是否为诱饵有关,因为被拦截的可能是被识别为弹头的诱饵,因而需考虑弹头类型事件。
真实弹头(或者拦截弹)可靠性事件是一个随机二值事件,要么可靠,要么不可靠,依概率收敛于期望。可靠性函数hr为随机变量xr的函数。即:
类似还存在: 弹头发现事件的函数hdw为随机变量xdw的函数,弹头跟踪事件的函数htw为随机变量xtw的函数,弹头识别事件的函数hiw为随机变量xiw的函数,一枚真实弹头被一枚拦截弹拦截的事件的函数hkwone为随机变量xkw的函数,弹头类型事件的函数htpw为随机变量xtp的函数等。重诱饵和轻诱饵也存在与上述弹头事件类似的事件。
突防概率有2种仿真方式:一种是对发射的所有弹头在突防各环节进行整体处理,即齐射式的仿真;第2种是对发射的所有弹头逐个进行完整突防过程处理,即顺序式的仿真。下面分别给出仿真框架:
考虑齐射式拦截,发现、跟踪、识别、拦截每一个环节都需要对所有弹头进行整体处理,处理完一个环节后再处理下一个环节。一次仿真过程包括步骤如下:
(1) 首先考虑可靠性事件,经可靠性处理后原有弹头w,α,β中可靠的弹头数为m1w,m1h,m1l。
(2) 接着考虑发现、跟踪、识别事件(即处理发现、跟踪、识别环节),处理后得到成功识别的弹头数为m2w,m2h,m2l。
(3) 接着考虑拦截事件(即处理拦截环节),分2种情况:当m2n≤N(m2=m2w+m2h+m2l)时,拦截弹足够;当m2n>N时,拦截弹不足,需考虑弹头类型事件。得到被拦截的弹头数为m3w,m3h,m3l。
(4) 最后得到n拦1策略的突防真实弹头数hw=m1w-m3w。
考虑顺序式拦截,总的突防弹头数由各枚突防弹头累加得到。当一枚弹头是真实弹头,可靠且没有被拦截,则该枚弹头实现突防。那么突防的真实弹头总数为

(2)
式中:x为识别为弹头的真实弹头数量;y,z为识别为弹头的重诱饵,轻诱饵的数量;htpwi为弹头类型函数。
根据n拦1策略,弹头被拦截事件的函数hki与可靠性函数、发现函数、跟踪函数、识别函数、单枚拦截弹的拦截函数和可靠性函数,以及拦截弹存在函数有关(max函数描述n拦1策略下n枚拦截弹只需其中有1枚实现拦住即可):
hki=max{hkwonejhrdfj,j=1,n}f(Ni).
(3)
而xd为未经拦截过程直接突防的真实弹头数,与x,y,z取值有关:

(4)
拦截弹存在函数f为
式中:Ni表示拦截第i枚弹头前所剩余的拦截弹数量。剩余的拦截弹数与识别为弹头事件的二值函数hisw相关,它是随机变量xtp和弹头、诱饵的发现、跟踪、识别事件的函数。
2 解析和仿真计算结果差异分析
2.1 预警和拦截过程的非独立性影响
考虑前述算例(a),根据式(1)计算得到突防概率为0.1。而仿真计算无论是齐射式仿真还是顺序式仿真结果都是0.135。在齐射式仿真中,总弹头10枚,因为可靠性为1.0,那么10枚弹头都可靠。对于发现概率0.9,因为发现事件是随机的,那么在一次实验中的发现弹头数可能是9,也可能是其他值,而样本集的均值能依概率收敛于9,但是对于单个样本(单次实验得到的结果)来说,其值不一定是9,也有可能是10,8,7,又因为拦截概率为1,拦截弹数为9,那么最多能拦截的弹头数是9枚,所以可能被拦截的弹头数会是9,8,7,而不可能是10,于是拦截过程会带通地把所有发现弹头数大于9的随机事件排除,那么对于样本集来说,发现弹头数为10的情况相当于仅发现9枚的情况,因此拦截弹不足(即攻击弹头的饱和)导致的结果相当于发现弹头数无法依概率收敛到9。说明攻击弹头饱和(当拦截弹不足)时,发现事件与拦截事件是相关的,而不是独立的。
在顺序式仿真中,总弹头数10枚,对于第1枚弹头,必然可靠,可能被发现也可能不被发现,被发现后消耗一枚拦截弹并确定被拦截,第2~9枚弹头类似,可能被发现也可能不被发现,发现即被拦截,但对于第10枚弹头来说,发现了也可能不被拦截,如果前面拦截弹已经使用完了,那么自然就无法拦截。因此被拦截的弹头数量最大只能是9,而且一定会存在小于9的情况,因为随机发现事件必然会出现发现弹头数小于9比如8,7等情况,因此被拦截弹头数的期望必然会小于9,突防弹头数必然大于1。同样说明了发现事件与拦截事件的非独立性。
而对于解析计算来说,发现事件和拦截事件是确定独立的,发现概率是0.9,那么解析计算一定是发现9枚弹头,并且因为拦截概率等于1,解析计算也一定是9枚弹头被拦截,剩下1枚弹头突防。
上述分析表明,预警过程发现环节的事件与拦截过程的事件间的非独立性会导致仿真结果与解析计算结果的差异,同样可以推论: 跟踪、识别等与发现环节性质类似的事件也会带来相同影响。
2.2 算例分析
仍然利用算例(a)来分析预警和拦截过程各环节的独立性。图1给出了拦截弹可靠性为0.9,其他概率为1时的突防概率,横轴为拦截弹数量,纵轴为突防概率。随着拦截弹头数增加,突防概率逐渐下降到0.1,当拦截弹数量达到10后,突防概率维持0.1不变,因为所有的弹头均已拦截,剩余的拦截弹不再使用。解析计算、齐射式仿真、顺序式仿真三者结果完全一致,根据解析计算的独立性,说明当拦截弹可靠性为0.9,其他概率为1.0时,预警和拦截过程各个环节是独立的。图2给出了拦截弹可靠性为0.9,拦截概率为0.9,其他概率为1时的突防概率,其结果与图1类似,说明拦截弹可靠性和拦截概率的变化不影响各环节的独立性。

图1 突防概率(Pr=0.9)Fig.1 Penetration probability(Pr=0.9)
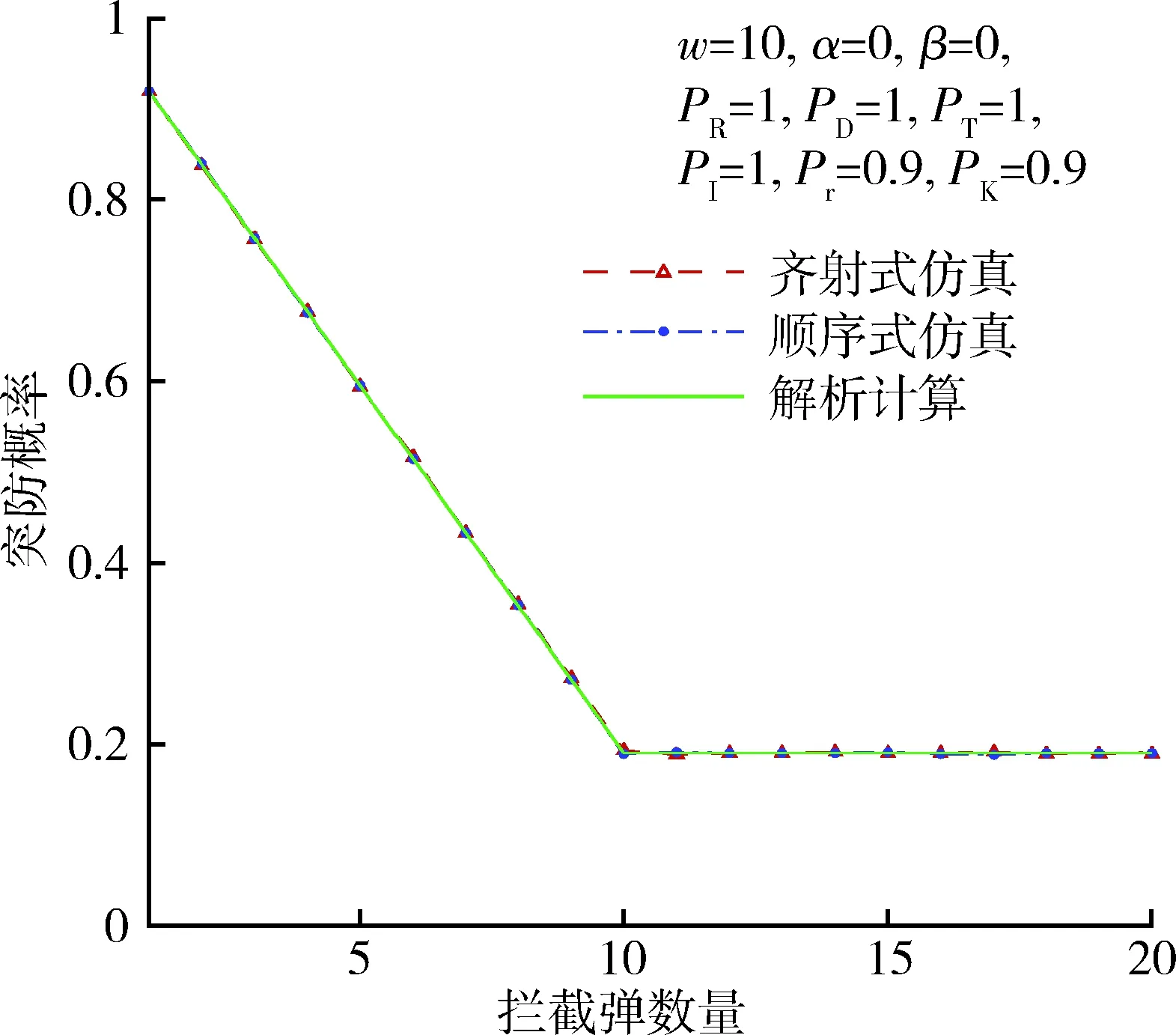
图2 突防概率(Pr=0.9,PK=0.9)Fig.2 Penetration probability(Pr=0.9,PK=0.9)
图3给出了拦截弹可靠性为0.9,拦截概率为0.9,弹头可靠性为0.9,其他概率为1时的突防概率,图中在拦截弹数为9时,仿真结果和解析计算结果存在明显差异,当拦截弹数为8时存在细微的差异。说明攻击弹头略饱和时弹头可靠性影响了各环节的独立性。图4给出了拦截弹可靠性为0.9,拦截概率为0.9,弹头识别概率为0.9,其他概率为1时的突防概率,其结果与图3类似,说明识别概率也带来相同的影响。因为发现、跟踪与识别环节的性质类似,可以推论发现、跟踪概率也将产生同样的影响。
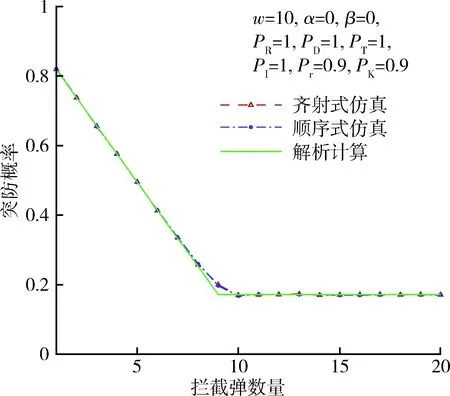
图3 突防概率(Pr=0.9,PK=0.9,PR=0.9)Fig.3 Penetration probability(Pr=0.9,PK=0.9,PR=0.9)
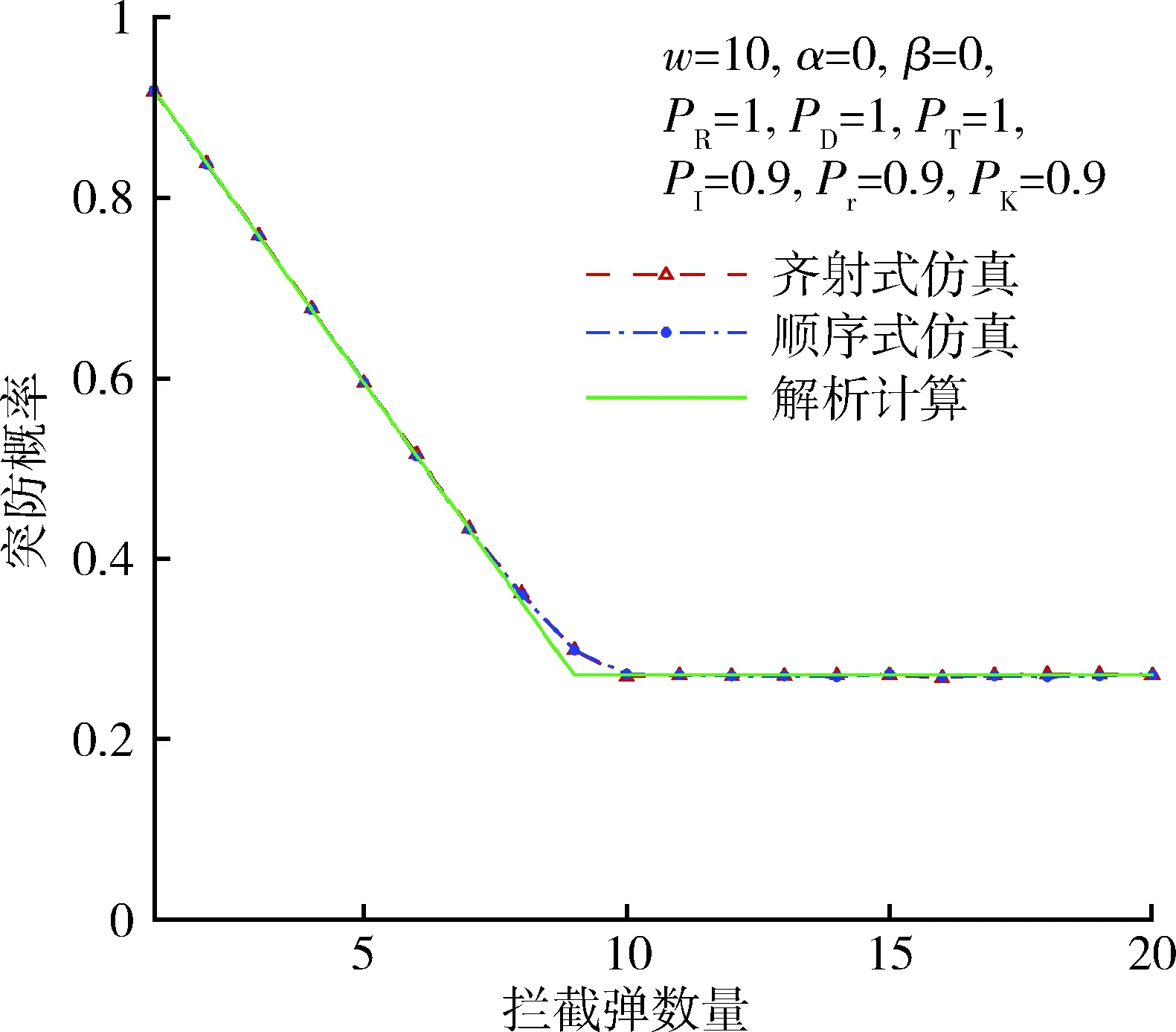
图4 突防概率(Pr=0.9,PK=0.9,PI=0.9)Fig.4 Penetration probability(Pr=0.9,PK=0.9,PI=0.9)
图5给出了弹头识别概率为0.9,其他概率为1.0时的突防概率,进一步验证识别概率会影响独立性,而拦截概率和拦截弹的可靠性则不会。总的来说:当攻击弹头略饱和时,弹头的可靠性、发现概率、跟踪概率、识别概率对预警和拦截过程各环节的独立性存在影响,而拦截概率和拦截弹可靠性则没有。

图5 突防概率(PI=0.9)Fig.5 Penetration probability(PI=0.9)
2.3 数学验证
从上述算例可知,当PR,PD,PT,PI存在小于1的情况时,仿真和解析计算差异主要发生在N=n(A-1)附近,即攻击弹头略饱和(拦截弹头略不足)时。利用一个更为简化的算例(b)来对顺序式仿真进行数学分析,考虑弹头数w=3,诱饵数为0,PD=0.9,其他概率值都等于1,n=1,那么式(2),(3)可以改写为

(5)
进一步展开为
hw= 1-hdw1f(N)+1-hdw2f(N-hdw1)+
1-hdw3f(N-hdw1-hdw2).
(6)
计算得到A=2.7,即当拦截弹数N=A-1=1.7附近会存在差异,因此考虑计算拦截弹数N为1~4的情况进行分析。当N=4时,hw的数学期望(均值)为
E(hw)= 1-E(hdw1f(4))+1-E(hdw2f(4-
hdw1))+1-E(hdw3f(4-hdw1-hdw2)).
因为4≥1,4-hdw1≥1,4-hdw1-hdw2≥1;
所以E(hw)=1-E(hdw1)+1-E(hdw2)+1-E(hdw3),
E(hw)=1-PD+1-PD+1-PD=0.3,
P=E(hw)/w=0.1.
该结果与式(1)的结果一致。
当N=3时,得到类似的结果:
E(hw)= 1-E(hdw1f(3))+1-E(hdw2f(3-
hdw1))+1-E(hdw3f(3-hdw1-hdw2))·
因为3≥1,3-hdw1≥1,3-hdw1-hdw2≥1;
所以E(hw)= 1-E(hdw1)+1-
E(hdw2)+1-E(hdw3),
E(hw)=1-PD+1-PD+1-PD=0.3,
P=E(hw)/w=0.1.
当N=2时,情况有所不同:
E(hw)= 1-E(hdw1f(2))+1-E(hdw2f(2-
hdw1))+1-E(hdw3f(2-hdw1-hdw2)),
因为2≥1,2-hdw1≥1,2-hdw1-hdw2?≥1.
因为f的参数值与hdw相关,不全大于1,所以求期望时可利用全概率公式计算:
P(hdw1= 1,hdw2=1)E(hw)=
0.81×(1-1+1-1+1-0)=0.81;
P(hdw1= 1,hdw2=0)E(hw)=
0.09×(1-1+1-0+1-0.9)=0.099;
P(hdw1= 0,hdw2=1)E(hw)=
0.09×(1-0+1-1+1-0.9)=0.099;
P(hdw1= 0,hdw2=0)E(hw)=
0.01×(1-0+1-0+1-0.9)=0.021;
E(hw)=1.029;
P=E(hw)/w=0.343.
当N=1时,也有:
E(hw)= 1-E(hdw1f(1))+1-E(hdw2f(1-hdw1))+
1-E(hdw3f(1-hdw1-hdw2)),
1≥1,1-hdw1?≥1,1-hdw1-hdw2?≥1;
P(hdw1=1,hdw2=1)E(hw)=
0.81×(1-1+1-0+1-0)=1.62;
P(hdw1=1,hdw2=0)E(hw)=
0.09×(1-1+1-0+1-0)=0.18;
P(hdw1=0,hdw2=1)E(hw)=
0.09×(1-0+1-1+1-0)=0.18;
P(hdw1=0,hdw2=0)E(hw)=
0.01×(1-0+1-0+1-0.9)=0.021;
E(hw)=2.001;
P=E(hw)/w=0.667.
从式(1)计算得到N=2,N=1时的P为
P(N=2)=0.333 333 333,
P(N=1)=0.666 666 666.
说明当N=2时,两者差异明显;N=1时,两者有略微的差异。
从结果看,因为仿真过程是1枚接1枚的拦截,所以前面处理的弹头是否发射拦截弹会影响后面弹头的拦截,这可能会构成一种条件概率。当攻击弹头数不饱和时(即拦截弹足够多,比如N≥nA时),无论前面拦截过程是什么情况,后面的拦截弹头都足够,这样识别事件和拦截事件互相独立,那么期望计算不考虑条件概率。但在攻击弹头数略饱和时(即拦截弹数量略少于需求拦截弹数,比如N=n(A-1)时),前面弹头的拦截情况使得后面弹头面临的拦截弹有可能足够,也有可能不足,这就导致期望值处于拦截弹足够和不足2种情况之间,计算需要考虑条件概率,这进一步体现了此时预警和拦截过程各个环节的非独立性。相比之下,在解析计算中拦截弹不足就是不足,因为各环节是互相独立的,其期望无需考虑条件概率。仿真计算和解析计算的差异就在于此,这也说明仿真计算能够考虑预警和拦截过程各环节互相影响的事实。
3 结束语
本文建立了弹道导弹突防各阶段统一的解析计算和蒙特卡罗仿真计算模型,通过算例比较,分析了攻击弹头略饱和时2种模型计算结果的差异,得出结论如下: 当攻击弹头数不饱和(即拦截弹数量足够时),预警和拦截过程的各个环节是独立的,解析计算和仿真计算结果一致,但是当攻击弹头数饱和时,各环节不再具有独立性,这导致了解析计算和仿真计算结果的差异。在实际应用中,因为仿真计算模型能考虑到各环节非独立性问题,所以更接近真实情况,从结果正确性角度考虑,决策者应以仿真结果作为参考依据。
