附加攻角效应对颤振稳定性能影响

欧阳克俭，陈政清

(1.国网湖南省电力公司电力科学研究院，长沙 410007;2.湖南大学风工程研究中心，长沙 410082)

附加攻角效应对颤振稳定性能影响

欧阳克俭1，陈政清2

(1.国网湖南省电力公司电力科学研究院，长沙 410007;2.湖南大学风工程研究中心，长沙 410082)

用强迫振动装置识别攻角从－3°～+4°细化步长变化为1°的洞庭湖二桥主梁断面气动导数;将该气动导数拟合成折减风速、攻角的三维曲面，只需获取某一有效攻角的具体数值即可自动求得所有气动导数值。通过在ANSYS中的三维TABLE表存储各攻角的气动导数，自动计入附加攻角对颤振稳定性影响。全模态颤振分析结果表明，附加攻角效应可降低该类桥梁的颤振临界风速。若按常规试验方法以3°攻角为步长进行气动导数插值计算，颤振分析有可能得到错误结论。

大跨桥梁;颤振;附加攻角;强迫振动;ANSYS

附加攻角一般认为桥梁断面在静风荷载作用下的扭转角度，存在于桥梁风工程中的风洞试验、气弹流固耦合CFD模拟中［1］。对苏通大桥进行全桥气弹模型试验时发现，接近颤振失稳临界状态［2］的附加攻角达5°。曹丰产等［3］通过节段模型试验对附加攻角进行研究。针对国内14座不同桥型、跨径桥梁的试验分析发现，节段模型附加攻角大小与扭矩系数斜率密切相关，接近颤振临界状态时西侯门桥附加攻角达2.7°。朱青等［4］针对节段模型试验存在附加攻角问题，设计出附加攻角测量、修正装置。试验研究知，附加攻角对扭转阻尼有一定影响，附加攻角修正后的模型颤振临界风速高于修正前;人为初始激励在0°风攻角对有效攻角影响非常明显;附加攻角使气动导数A2、A1、H3显著变大，从而提高颤振临界风速。因此进行三维颤振分析时，若气动导数按初始攻角取值，则与桥梁实际有效攻角间有较大误差。应对桥梁在静风荷载作用下的有效攻角如实评判后再取桥梁结构有效攻角对应的气动导数进行相关颤振分析。文献［5－8］在三维颤振分析中考虑附加攻角造成的气动力非线性对颤振稳定性影响，用气动导数插值方法处理。对气动导数处理，由于通常不考虑附加攻角修正值及存在两插值攻角间步长过宽，因而导致插值计算误差过大。本文以斜拉悬索桥洞庭湖二桥方案桥(简称洞庭湖二桥)为例开展附加攻角效应研究。

1 静风附加攻角

由于桥梁结构在颤振前后始终作用静风荷载，颤振发生前有小于颤振临界风速的静风荷载。在其作用下结构会发生几何变形，进而导致主梁攻角发生改变，见图1，其中θ0为初始攻角;θ为在桥面施加静风荷载U后结构的有效攻角;α为静风荷载引起结构变形的附加攻角。

图1 附加攻角示意图Fig.1 Schematic additional angle of attack

为在数值计算中有效评估附加攻角对颤振影响，需用含攻角信息的气动导数反应气动力。在有限元计算中考虑静风荷载对附加攻角影响需采用内外两重迭代方法，引入松弛因子易于快速得到收敛解，本文中松弛因子取0.4。静风荷载有限元理论计算见文献［9］。洞庭湖二桥主梁断面见图2，节段模型缩尺比1:80，试验获得风轴坐标系下三分力系数见图3。

图2 洞庭湖二桥成桥状态模型断面Fig.2 Completed model section of Dongting lake bridge

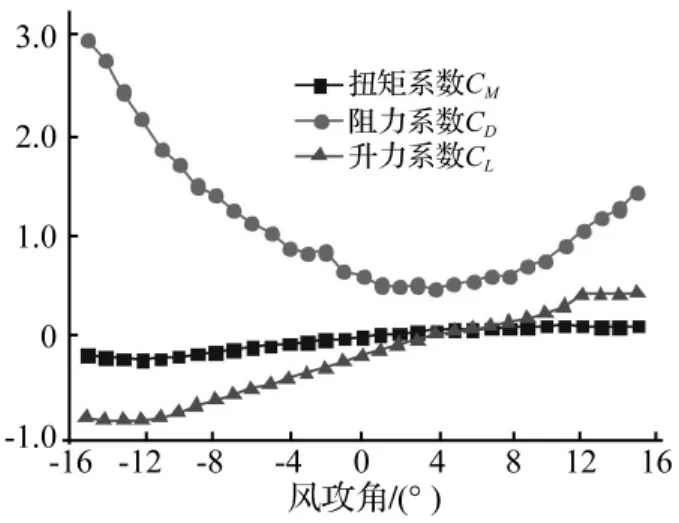
图3 洞庭湖二桥风轴三分力系数Fig.3 Third axis wind force coefficient of Dongting lake bridge

2 加密攻角步长变化的气动导数识别试验

在已知节段模型三分力系数前提下，由于在不同风速下静力平衡时阻尼力不起作用，故可通过理论计算获得节段模型的附加攻角，即

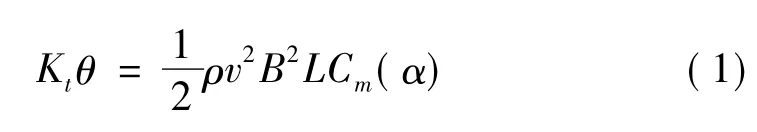
式中:Kt为模型抗扭刚度;θ为附加攻角;α为实际攻角;B，L分别为模型宽度及长度。

由式(1)可知自由振动识别的气动导数本身含附加攻角效应影响，若在此基础上插值计算附加攻角对应的气动导数则会有偏差。而对弹性悬挂节段模型进行气动导数识别时所给模型的初始激励有较大人为因素，难以控制，故初始激励影响、造成附加攻角变化及附加攻角影响会极大降低自由振动识别气动导数的准确性。此时应选用强迫振动法以克服自由振动法中存在的静风附加攻角问题［10－12］，并以攻角变化1°为一个步长进行气动导数识别，可降低不同攻角气动导数插值的误差。只有在有限元数值计算中考虑附加攻角影响才能有效计算桥梁结构的颤振临界风速。

本文以主跨径1 800 m的洞庭湖二桥为研究对象，在湖南大学－Ⅱ号风洞低速段进行－3°，－2°，－1°，0°，+1°+2°，+3°，+4°计8个工况的强迫振动气动导数识别试验。具体参数见表1。

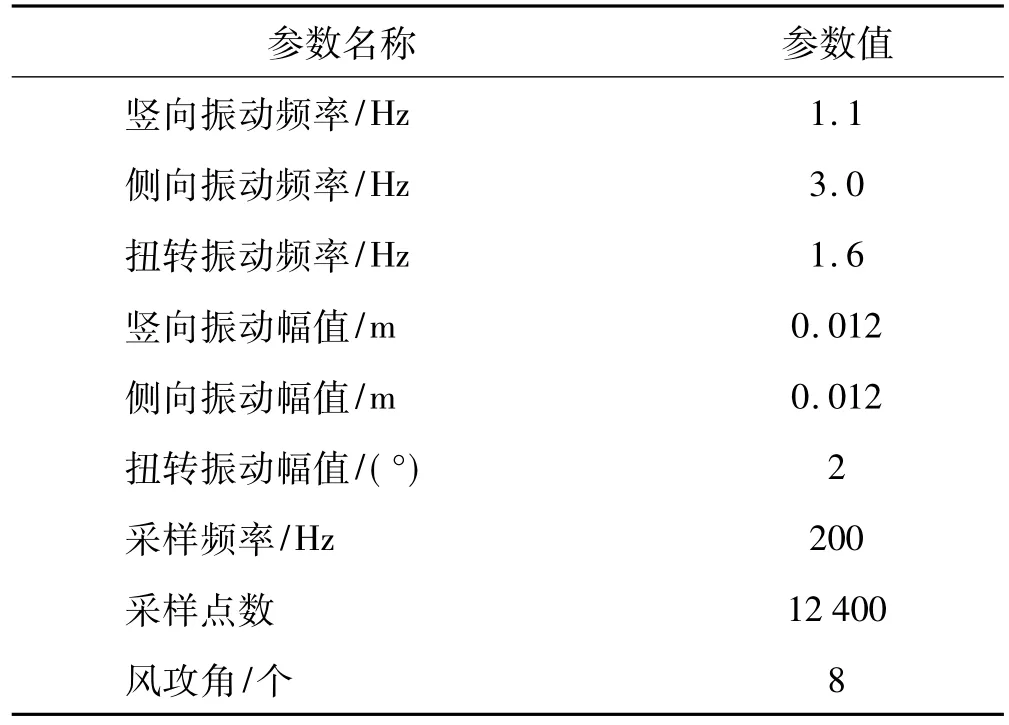
表1 附加攻角强迫振动试验参数Tab.1 Additional angle of attack for forced vibration test parameters

图4 成桥状态节段模型强迫振动试验Fig.4 Completed bridge section model forced vibration tests

经强迫振动试验识别洞庭湖二桥断面在8个不同攻角下的气动导数，振动形式为三自由度耦合振动，成桥状态节段模型强迫振动试验见图4。图5为不同攻角在折减风速为9.85时A的数值变化。由图5看出，随攻角由负变正A2值逐渐变大，说明攻角越大断面流线性能越差。图中虚线表示若在0°、+3°，0°、－3°，0°、+4°之间继续用线性差值法，A值则会产生较大误差，从而影响颤振分析。H及A(i=14)随攻角变化对比见图6，将不同攻角下同一气动导数值用二元插值拟合成一个曲面见图7，并编制计算程序，只需获取某一有效攻角值即可自动求得所有气动导数值。由图6、图7看出，H及A(i=14)随攻角由负变正均有一定规律性:低折减风速下气动导数变化不明显，随折减风速增大，各不同攻角下气动导数差值较明显，A，A，A，H随攻角由负变正气动导数值逐渐变小，A，H随攻角由负变正气动导数值逐渐变大。而量级较小的A随攻角变化也体现出较好的规律性，说明强迫振动试验精度能得到有效保障。

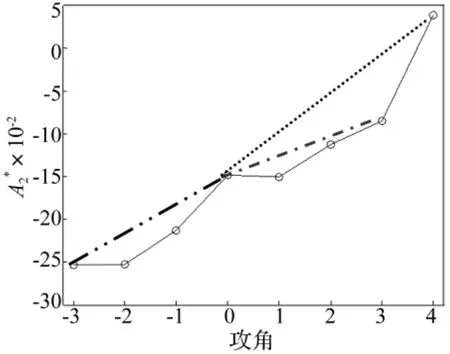
图5 不同攻角A2值Fig.5 Different A2values of the angle of attack

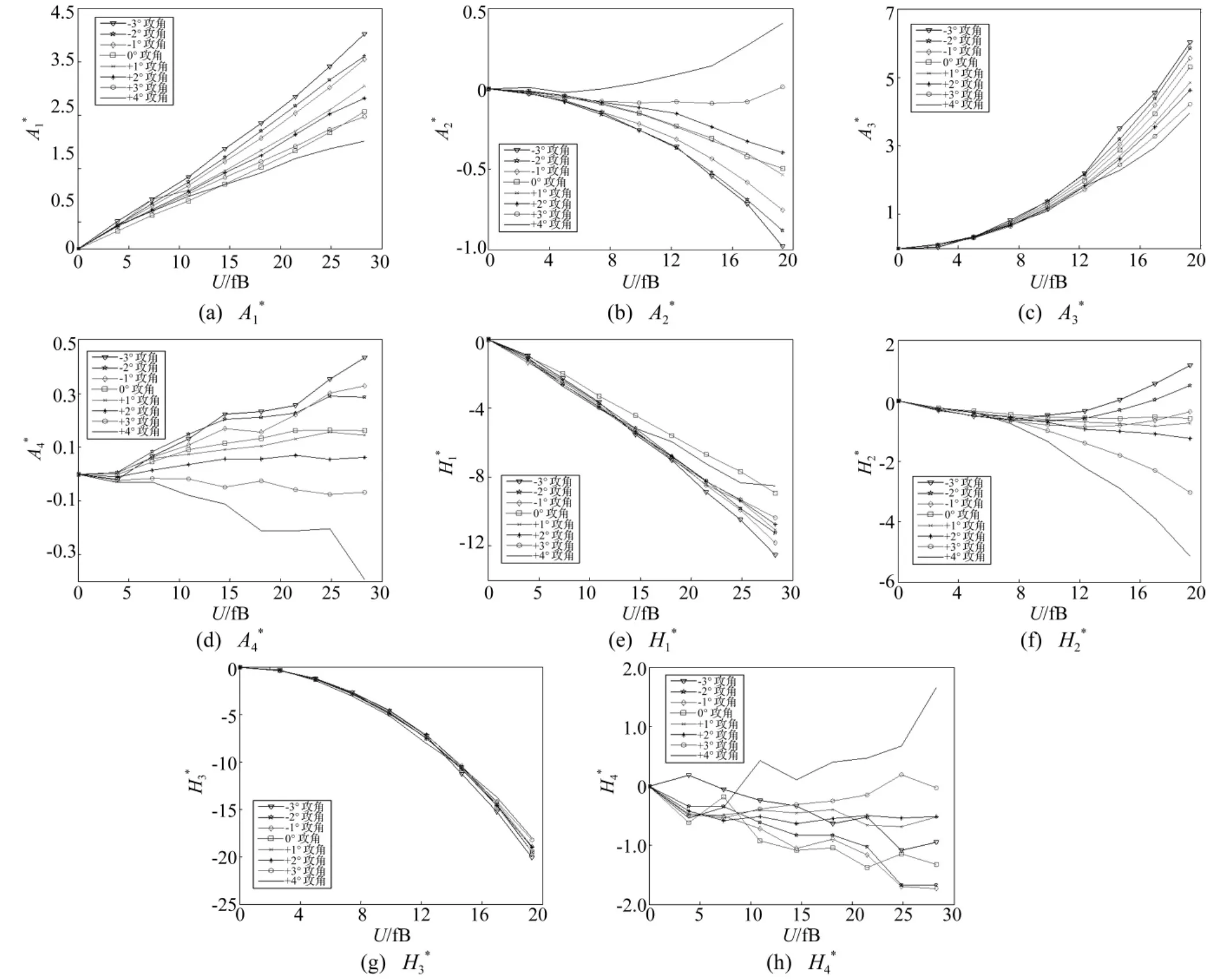
图6 不同攻角下洞庭湖二桥气动导数对比Fig.6 Different angle of attack aerodynamic derivatives contrast of Dongting Lake bridge

3 附加攻角效应数值计算

岳阳洞庭湖二桥方案桥为斜拉－悬索协作体系，跨径为310 m+1800 m+310 m。两310 m边跨为双索面斜拉区，主梁用混凝土箱梁，斜拉索间距12 m。主跨1800 m采用斜拉－悬索协作体系，悬吊区长1168 m，斜拉区长度388 m，拉吊结合区长72 m，桥型布置见图8。

静风荷载对颤振临界风速影响主要表现为:①对结构动力特性产生影响。在基于ANSYS进行颤振分析时需选用有预应力的模态分析求解器，有效计入静风荷载及结构自重对动力特性影响;②主梁发生扭转变形时产生的附加攻角必改变风桥的流固耦合机制，影响颤振性能。

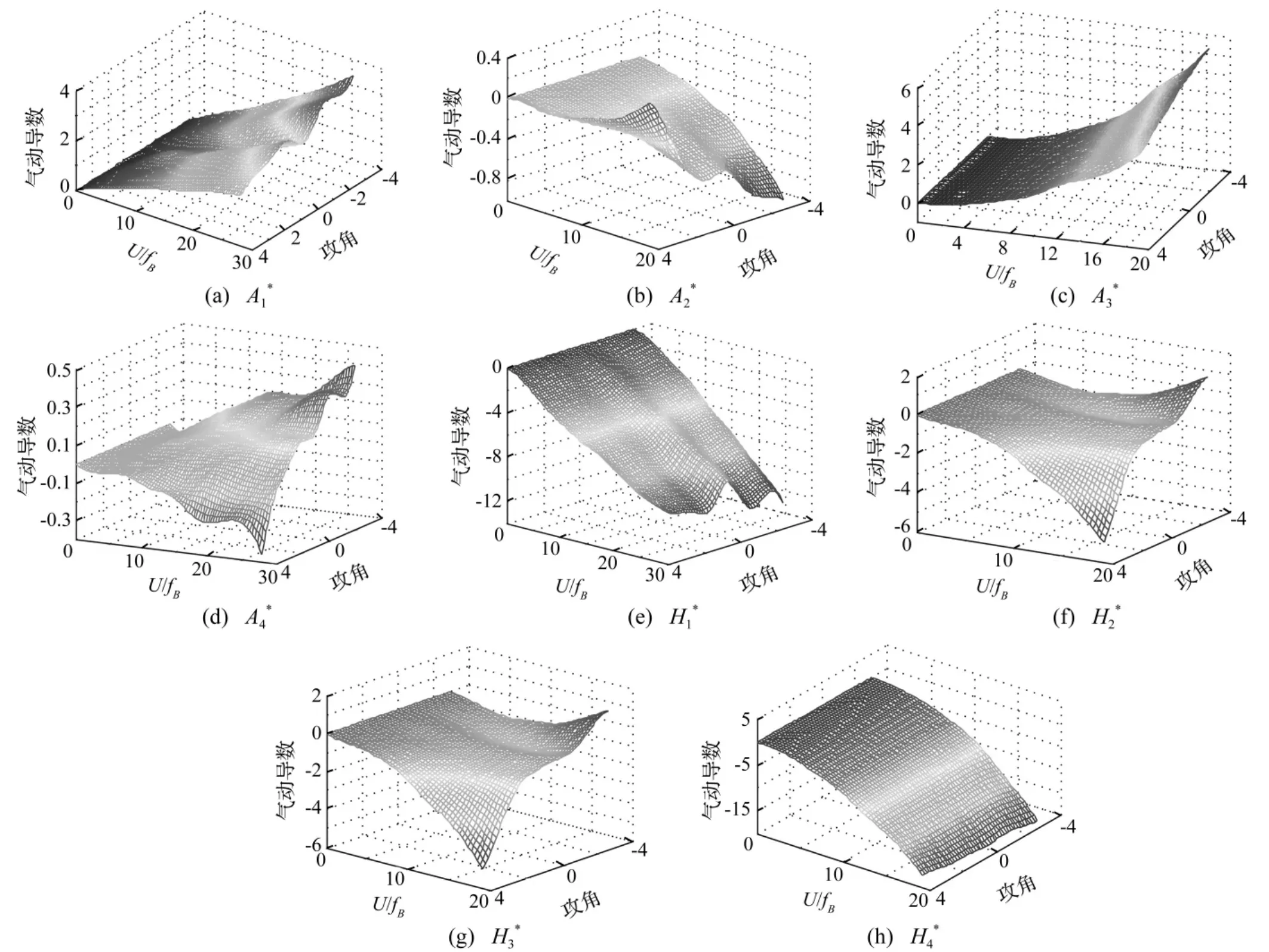
图7 不同攻角下气动导数拟合曲面Fig.7 Fitting surface of different angles of attack aerodynamic derivatives

图8 洞庭湖二桥桥型布置Fig.8 Type layout of Dongting lake bridge

为在ANSYS全模态颤振分析中有效考虑附加攻角对颤振性能影响［13－15］，本文利用ANSYS中TABLE表的行、列、面三维数组功能存储不同攻角气动导数。TABLE表每个面存储一个攻角气动导数，每行存储一个折减风速对应不同气动导数。将不同攻角定义为面的下标，在获得每一特定风速对应的附加攻角及折减风速时即可用TABLE表的线性插值功能自动获得任意有效攻角对应的气动导数，程序实现非常方便。TABLE表具体设置见图9，其中“ANGLE”对应的第一行为面的下标即有效攻角。“WIND”对应的第一列为折减风速。洞庭湖二桥是否考虑附加攻角效应的颤振临界风速、颤振频率对比见表2。由表2看出，由于0°攻角在颤振临界风速前的附加攻角较小，由附加攻角效应引起的颤振性能改变不大。尽管+3°攻角、0°攻角在不考虑附加攻角时的颤振临界风速基本相等，但由于桥梁断面在+3°攻角时对应的升力矩系数较大，引起的附加攻角亦较大，对颤振临界风速改变较显著。

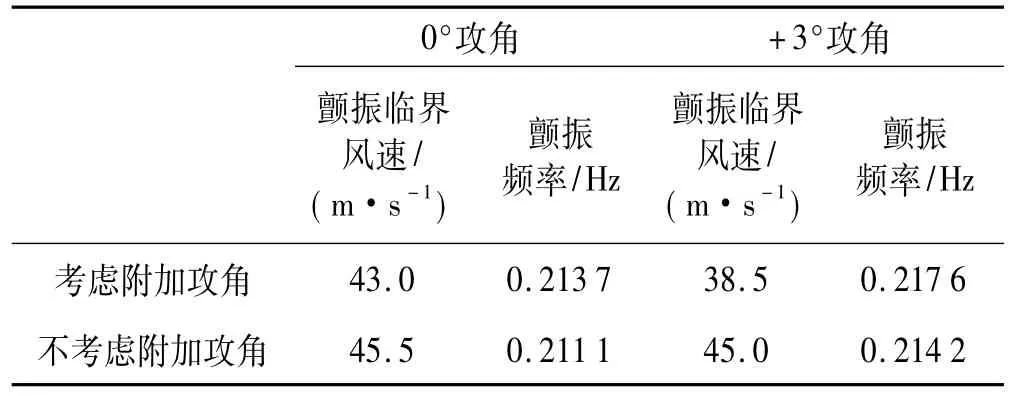
表2 附加攻角效应颤振分析结果对比Tab.2 The results comparing of additional effects of angle of attack flutter analysis

图10、图11分别为0°及+3°两攻角在计及附加攻角效应时的颤振形态。由两图看出，两攻角的颤振形态较接近，为弯扭耦合振型。对该类桥梁断面形式，附加攻角起到降低颤振临界风速作用，因此在桥梁抗风设计中需充分考虑附加攻角对颤振影响，否则会得到偏危险结论。

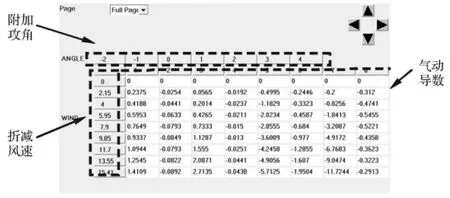
图9 ANSYS三维数据表Fig.9 Three－dimensional data table of ANSYS

图100 °攻角颤振形态图Fig.10 0°Angle of attack flutter modality map

图11 +3°攻角颤振形态图Fig.11+3°Angle of attack flutter modality map

4 结论

(1)利用强迫振动装置识别由－3°～+4°攻角、步长为1°的洞庭湖二桥主梁断面气动导数。直接用两间距过大攻角插值计算所得有效攻角气动导数会有较大误差。

(2)用二元插值将不同攻角下同一气动导数值拟合成一个曲面，只需获取某有效攻角的具体数值即可自动求得所有气动导数值。H，A(i=14)随攻角由负变正时在低折减风速下气动导数变化不明显;折减风速增大A，A，A，H随攻角由负变正气动导数值逐渐变小;A，H随攻角由负变正气动导数值逐渐变大。对量级较小的A随攻角变化的规律性较好。

(3)在ANSYS中用三维TABLE表存储不同攻角的气动导数值，能自动计入附加攻角效应导致的气动力非线性对颤振稳定性影响。附加攻角能降低颤振临界风速作用，桥梁抗风设计中应充分考虑附加攻角对颤振影响。

［1］Boonyapinyo V，YamadaH，MiyataT.Wind－induced nonlinear lateral－torsional buckling of cable－stayed bridges［J］.Journal of Structural Engineering，1994，120(2):486－506.

［2］许福友，陈艾荣.苏通大桥气弹模型气动失稳分析［J］.土木工程学报，2007，40(7):44－48.

XU Fu－you，CHEN Ai－rong.Analysis of the aerodynamic divergence of an aeroelastic model of Sutong bridge［J］. China Civil Engineering Journal，2007，40(7):44－48.

［3］曹丰产，葛耀君.桥梁节段模型试验的风攻角与静力扭转发散［C］.第十二届全国结构风工程学术会议论文集［A］.西安:2005:302－306.

［4］朱青，朱乐东，郭震山.节段模型静风附加攻角对颤振性能的影响［C］.第十四届全国结构风工程学术会议论文集［A］.北京:2009:719－724.

［5］刘慕广，陈政清.典型钝体断面大攻角下的颤振自激力特性［J］.振动与冲击，2013，32(10):22－25.

LIU Mu－guang，CHEN Zheng－qing.Characteristcs of selfexcited forces in flutter of typical blunt body under large attack angles［J］.Journal of Vibration and Shcok，2013，32(10):22－25.

［6］许福友，陈艾荣.苏通大桥三维颤振分析［J］.工程力学，2008，25(8):139－144.

XU Fu－you，CHEN Ai－rong.3－D flutter analysis of sutong bridge［J］.Engineering Mechanics，2008，25(8):139－144.

［7］丁泉顺，王景，朱乐东.桥梁断面颤振导数识别的耦合自由振动方法［J］.振动与冲击，2012，31(24):5－8.

DING Quan－shun，WANG Jing，ZHU Le－dong.Coupled free vibration technique for identifying flutter derivatives of bridge decks［J］.Journal of Vibration and Shcok，2012，31(24):5－8.

［8］郭增伟，赵林，葛耀君，等.基于桥梁断面压力分布统计特性的抑流板抑制涡振机理研究［J］.振动与冲击，2012，31(7):89－94.

GUO Zeng－wei，ZHAO Lin，GE Yao－jun，et al.Mechanism analysis for vortex－induced vibration reduction of a flat streamlined steel box－shaped girder with airflow－suppressing board based on statistical property of surface pressure［J］. Journal of Vibration and Shcok，2012，31(7):89－94.

［9］陈政清.桥梁风工程［M］.北京:人民交通出版社，2005.

［10］Miyata T，Yamada H.On an application of the direct flutter FEM analysis for long－span bridges［C］.In:Proc 9th Int Conf on Wind Engineering，New Delhi.，1995:1033－1041.

［11］Ge YJ，XiangHF.Recentdevelopmentofbridge aerodynamics in China［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96:736－768.

［12］欧阳克俭.气动力有理函数与颤振稳定性的多因素分析［D］.长沙:湖南大学，2011.

［13］Hua X G，Chen Z Q，Ni Y Q，et al.Flutter analysis of longspan bridges using ANSYS［J］.Wind and Structures，2007，10(1):61－82.

［14］Matsumoto M，Shirato H，Shijo R，et al.Flutter stabilization of long span bridges［C］.In:Proc of the 2ndInternational Symposium on Advances in Wind and Structures，2002:62－66.

［15］Ding Q，Chen A，Xiang H.Coupled flutter analysis of longspan bridges by multimode and full－order approaches［J］. Journal of Wind Engineering and Industrial Aerodynamics，2002，90(12):1981－1993.

Influence of static wind additive attack angle on flutter performance of bridges

OUYANG Ke－jian1，CHEN Zheng－qing2
(1.State Grid Hunan Electric Power Corporation Research Institute，Changsha 410007，China; 2.Wind Engineering Research Center，Hunan University，Changsha 410082，China)

Aerodynamic derivatives of Dongting Lake bridge girder sections were identified by forced vibration in wind tunnel，with the angle of attack changing in step of 1°from－3°to+4°.The aerodynamic derivatives were fitted to form a three－dimensional surface made up by reduced velocity，angle of attack and aerodynamic derivatives.Only if a specific value of the effective angle of attack is given，all aerodynamic derivatives can be automatically obtained.The data of aerodynamic derivatives were stored in a three－dimensional TABLE in ANSYS，the effect of additional angle of attack on flutter stability was naturally concerned.A full－mode flutter analysis indicate that the additional angle of attack may decline the critical flutter speed of typical bridges and the influenced extent is according to the type of bridges.

long－span bridge;flutter;additive attack angle;forced vibration;ANSYS

U446.1

A

10.13465/j.cnki.jvs.2015.02.008

国家自然科学基金重大研究计划(重大建筑与桥梁强/台风灾变的集成研究91215303)

2013－11－01修改稿收到日期:2014－01－28

欧阳克俭男，博士，工程师，1981年9月生邮箱:ouykj@126.com