空地多目标攻击武器-目标分配与制导序列优化
2023-09-07张安徐双飞毕文豪徐晗
张安, 徐双飞, 毕文豪, 徐晗
(西北工业大学 航空学院, 西安 陕西 710072)
0 引言
远距离空地多目标攻击是现代战争中的一种新型作战形式,我方攻击机编队携带并发射多枚、多种型号的空地导弹[1],各空地导弹由多个制导站接力制导[2],对敌方多个地面目标实施精确打击,具有打击范围更广、抗干扰能力更强的特点。为了提升打击成功率,并减少资源消耗,需要在一定的约束下,对各攻击机的打击目标、使用的空地导弹类型与数量,以及各导弹的接力制导方案等进行规划,即涉及武器-目标分配(WTA)和接力制导规划 2类问题。
WTA将有限的武器弹药,通过最优策略,分配到相关目标,实现作战效能最大化,是一种多参数、多约束、非线性优化问题[3-5]。传统WTA方法以解析法为主,包括分支定界法[6]、割平面法[7]、隐枚举法等,这些方法对复杂WTA问题的适用性较差。WTA智能优化方法是近年来的主要研究方法:夏维等[8]提出包含变量随机分解、合作协调进化和种群非支配排序的改进多目标粒子群优化算法,实现大规模WTA问题的实时求解;王然辉等[9]使用遗传算法求解对地打击WTA问题,并通过控制种群规模和改进变异策略,提升算法效率,避免算法早熟;Chang等[10]针对多阶段动态WTA问题,以最小化敌方目标的生存概率为优化目标,采用改进的人工蜂群算法进行求解。其他WTA智能优化方法还包括神经网络法[11]、K近邻算法[12]、强化学习算法[13]、布谷鸟算法[14]、模拟退火算法[15]等。当前关于WTA的研究大多对作战场景的设计较为简单,直接给定武器种类、数量以及对各目标的毁伤概率[16],忽略了作战环境及作战过程对打击效果的影响。在远距离空地多目标攻击中,WTA需要考虑目标位置、武器发射平台位置、不同武器发射平台的火力配置差异等因素,并与导弹的接力制导过程紧密结合。
规划各空地导弹由哪些制导站进行接力制导并规划制导次序,属于序列优化[17-18]问题。目前关于序列优化算法有一定的研究成果:Xu等[19]采用基于试飞任务序列的改进遗传算法,优化多架试验机的试飞任务编排;窦建平等[20]采用基于可行工序序列的遗传算法,对零件的加工工序和各工序匹配的机床、刀具等资源进行优化,这些研究方法对本研究具有指导意义。
本文研究针对远距离空地多目标攻击作战任务,设计更为复杂的作战场景:对传统WTA问题中的武器种类、数量、毁伤概率等因素进行扩展,考虑不同攻击机的导弹配置差异,以及各攻击机与各目标在战场中的位置分布,并在战场中加入制导单元,将WTA与空地导弹的飞行过程及接力制导过程紧密结合。建立多目标、多约束WTA与制导序列优化模型,目标函数为目标综合生存概率最小和总用弹量最少,约束条件涉及攻击机导弹配置、导弹毁伤能力、目标毁伤要求、制导站性能等。提出基于双序列编码的多种群带精英策略的非支配排序遗传算法(DSMPNSGA-Ⅱ),设计适用于WTA与制导序列优化模型的编码、解码、选择、交叉、变异等操作,并通过多种群策略提升解的质量。通过算例仿真与算法对比,验证DSMPNSGA-Ⅱ求解WTA与制导序列优化问题的有效性。
1 WTA与制导序列优化模型
1.1 作战场景构建
假设在未来某一远距离空地多目标攻击任务中,我方派出M架攻击机,每架攻击机携带一定数量的同种类型或不同类型的空地导弹,对敌方N个地面固定目标进行打击。我方已在战场部署K个地面固定制导站,各制导站的制导区域(在二维平面的投影)为以制导站为圆心的圆,每个制导站可承担多枚空地导弹的制导任务。作战区域为二维平面矩形区域。以矩形西北顶点为原点O,正东方向为x轴正方向,正南方向为y轴正方向,建立平面直角坐标系。作战场景如图1所示。
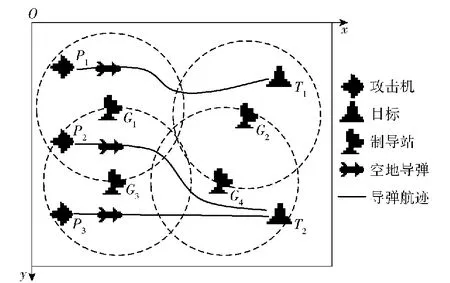
图1 作战场景示意图
图1表示我方派出3架攻击机P1~P3,对敌方2个地面目标T1和T2进行打击,由4个制导站G1~G4对导弹进行制导。目标T1由攻击机P1发射导弹进行打击,导弹由制导站G1和G2依次制导;目标T2由攻击机P2和P3发射导弹进行打击,两枚导弹分别由G1和G4、G3和G4依次制导。
本文研究假设:图1所示各攻击机位置即为该攻击机携带导弹的发射位置;各空地导弹在巡航平飞阶段高度一致,在该高度对应二维水平面内进行WTA与接力制导规划;两个制导站的制导区域有交集即可进行制导交接。WTA与制导序列优化问题需要在一定的约束下,对以下内容进行规划:
1)规划每个目标由哪些攻击机进行打击;
2)规划每架攻击机使用的导弹类型与数量;
3)规划各导弹由哪些制导站依次接力制导。
优化目的为提升对目标的整体毁伤概率,并减少资源消耗。
1.2 优化模型建立
1.2.1 模型参数定义
模型中的参数定义为:
1)攻击机参数。攻击机数量为M,第m架攻击机记为Pm,位置为ppm=(ppxm,ppym),引入攻击机导弹配置矩阵PM:
(1)
式中:pmm,h为第m行第h列元素,表示攻击机Pm装备第h种类型导弹的数量,取值范围为非负整数集,h=1,2,…,H,H为导弹类型数量。
2)目标参数。目标数量为N,第n个目标记为Tn,位置ptn=(ptxn,ptyn),价值系数为vn,各目标的最小毁伤概率均为dpm,对各目标的最大毁伤次数均为dnm。
3)制导站参数。制导站数量为K,第k个制导站记为Gk,位置为pgk=(pgxk,pgyk),制导区域为gxyk,各制导站制导半径均为RG,制导能力均为CG。
4)导弹参数。空地导弹数量等于PM中所有元素之和,记为sum(PM),导弹类型数量为H,第i枚导弹的类型为mtypei(取值为不超过H的正整数),所属攻击机为mpi(取值为不超过M的正整数),引入导弹杀伤概率矩阵MT:
(2)
式中:mth,n为第h行第n列元素,表示第h种类型导弹对目标Tn的杀伤概率,取值范围为实数集(0,1)。
5)其他参数:引入WTA矩阵PT和制导矩阵MG,作为本文研究的决策变量:
(3)
(4)
式中:pti,j为PT中的第i行第j列元素,取值为0或1,若取值为1则表示第i枚空地导弹攻击目标Tj,1在PT的每行元素中最多出现1次;MGi为第i枚导弹的制导序列,该导弹由制导站mgi,1、mgi,2、…、mgi,kmg(i)依次接力制导,kmg(i)表示为第i枚导弹进行制导的制导站数量,若该导弹不攻击任何目标则MGi=∅,kmg(i)为0。
目标综合生存概率为f1,总用弹量为f2,f1和f2作为目标函数。
1.2.2 目标函数
本研究考虑目标综合毁伤概率最大和总用弹量最少两个优化目标。为了使各目标函数优化方向一致(即均为最小值优化),用目标综合生存概率最小代替目标综合毁伤概率最大的优化目标。两个目标函数计算公式如下:
1)目标综合生存概率最小:
(5)
式(5)以目标的价值系数为权重,对各目标的毁伤概率进行线性加权求和,获得目标综合毁伤概率,进而计算目标综合生存概率,式(5)的推导过程见文献[8]。
2)总用弹量最少:
(6)
式(6)表示PT中所有元素之和为总用弹量。
1.2.3 约束条件
本研究考虑约束条件包括:决策变量取值范围约束、导弹攻击能力约束、目标最大毁伤次数约束、目标最小毁伤概率约束、制导区域约束、制导能力约束。
1)决策变量取值范围约束:
pti,j=0,1,i=1,2,…,sum(PM),j=1,2,…,N
(7)
(8)
式(7)表示PT中的元素取值为0或1;式(8)表示MG中元素的取值为制导站的编号,各制导站在同一导弹的制导序列中最多出现1次。
2)导弹攻击能力约束:
(9)
式(9)表示每一枚导弹最多攻击一个目标。
3)目标最大毁伤次数约束:
(10)
式(10)表示攻击每个目标的导弹数量最多为dnm。
4)目标最小毁伤概率约束:
(11)
式(11)表示每个目标的毁伤概率不小于dpm。
5)制导区域约束:
(12)
式(12)表示每一枚导弹所属攻击机的位置应在其制导序列第一个制导站的制导范围内;该导弹打击的目标应在其制导序列最后一个制导站的制导范围内;每个制导序列中相邻制导站的制导范围应有交集,以满足制导交接条件。
6)制导能力约束:
(13)
式中:fnum(x,y)表示x在向量y中出现的次数。式(13)表示每个制导站最多承担CG枚空地导弹的制导任务。
2 DSMPNSGA-Ⅱ原理
带精英策略的非支配排序遗传算法(NSGA-Ⅱ)[21]是目前最流行的多目标优化算法之一,具有运算速度较快、收敛性较好等优点,但也存在算法早熟、最优解多样性差的问题。本文需要对WTA方案和接力制导方案进行规划,求解空间以及约束条件都较为复杂。为将NSGA-Ⅱ合理应用于WTA与制导序列优化模型的求解,并克服传统NSGA-Ⅱ的算法早熟问题,本文提出基于双序列编码的多种群NSGA-Ⅱ。本节内容对DSMPNSGA-Ⅱ的关键步骤进行介绍,其中涉及非支配排序、拥挤距离计算、精英保留等操作与传统NSGA-Ⅱ相同,具体流程见文献[22]。
2.1 编码与解码
2.1.1 编码与解码基本步骤
设计种群中每个个体包含两条染色体,编码分别为st和sg。st为WTA序列,sg为制导站序列,两序列编码分别为
(14)
(15)
式(14)表示st中sti的取值为第i枚导弹的打击目标,若取值为0则该导弹不参与打击任务;式(15)表示每个制导站在sg中均出现CG次。
在编码时需初始化st中每个目标至少出现 1次(在目标最小毁伤概率约束下,各目标最少需要被攻击1次),最多出现dnm次。
解码过程如下所示:
1)对st进行解码,初始化PT中所有元素均为0,对于i=1,2,…,sum(PM),若sti≠0,则更新pti,n=1,其中n=sti;
2)根据式(10)和式(11)判断PT是否满足目标最大毁伤次数约束和最小毁伤概率约束,若不满足约束则赋值f1≫1、f2≫sum(PM),解码结束,否则继续解码sg,初始化l=1,执行步骤3;
3)根据PT确定第l枚导弹的攻击目标,若该导弹无攻击目标则跳转至步骤5,否则根据导弹发射位置(即所属攻击机位置)和目标位置,对sg的剩余制导站进行搜索,获得该导弹的制导序列MGl,若无可行制导序列,则赋值f1≫1、f2≫sum(PM),解码结束,否则执行步骤4;
4)将MGl中的制导站从sg中删除,每个制导站仅删除一次;
5)更新l=l+1;
6)重复步骤3~步骤5,直到l>sum(PM);
7)计算目标函数值f1和f2;
8)输出决策变量PT和MG,目标函数值f1和f2,解码结束。
在解码的步骤3中,导弹制导序列搜索方法为深度优先搜索-Dijkstra(DFS-DJ)算法。
2.1.2 空地导弹制导序列搜索方法
本研究提出DFS-DJ搜索方法,用于空地导弹制导序列搜索,实现制导站序列的解码。给定第l枚导弹所属攻击机位置、打击目标位置、剩余制导站序列sgl,制导序列搜索过程为:
1)对sgl进行去重,每个制导站仅保留第1次出现的位置,去重后的制导站序列为sgl′;
2)构建无向无权图Gdfs=〈Vdfs,Edfs〉,顶点集Vdfs中的元素依次为起始点(对应攻击机位置)、中间点(依次对应sgl′中的制导站位置)、目标点(对应目标位置),根据各制导站的制导区域是否覆盖攻击机与目标位置,以及制导区域是否有交集,构建边集Edfs;
3)对Gdfs进行深度优先搜索(DFS),获得制导区域连通起始点到目标点的制导站序列sgl″;
4)根据攻击机位置、目标位置和sgl″中的制导站位置重新构建无向无权图Gdj=〈Vdj,Edj〉,并采用Dijkstra算法[23]获得导弹的制导序列MGl。
Dijkstra算法能够获得导弹的最短制导序列,减少制导站的占用,提升后续导弹制导序列搜索的成功率。本研究在使用Dijkstra算法搜索之前先进行DFS,而不是直接使用Dijkstra算法,原因如下:
1)sgl中的制导站数量较多,对应搜索节点较多,导致Dijkstra算法运算速度较慢,通过DFS可以减少制导站数量,进而减少搜索节点数量,提升运算速度。
2)DSMPNSGA-Ⅱ旨在通过优化sg中制导站的次序来优化MG中各导弹的制导序列,Dijkstra算法在搜索过程中会遍历当前节点的所有相邻节点,sg中的制导站次序对Dijkstra算法结果影响较小,而对DFS结果影响较大,因此在Dijkstra算法前加入DFS算法,有利于提升DSMPNSGA-Ⅱ的搜索能力。
2.1.3 编码与解码示例
这里通过一个例子说明编码与解码的过程,如图2所示,本例包含3架攻击机、2个目标和4个制导站,设每个攻击机携带1枚导弹,CG为2。
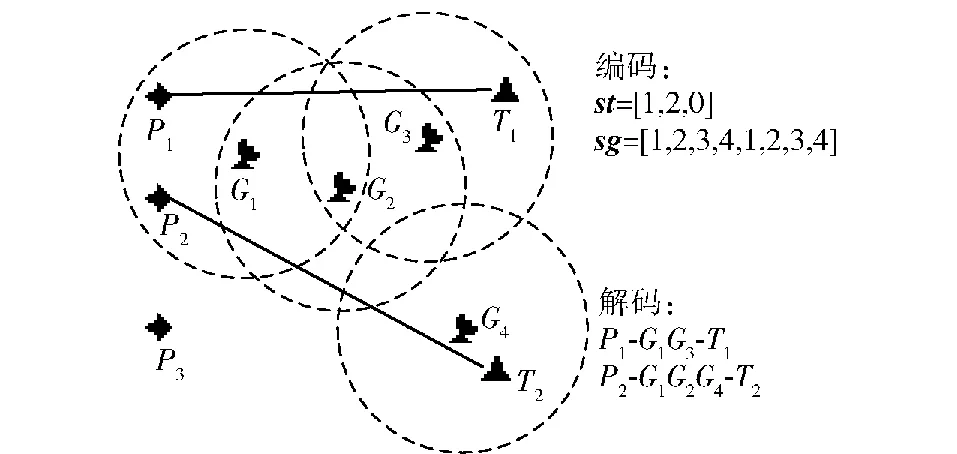
图2 编码和解码示意图
假设某一个体的两条染色体编码为st=[1,2,0]、sg=[1,2,3,4,1,2,3,4],解码过程如下:
1)根据st确定P1发射导弹打击T1,P2发射导弹打击T2,P3携带的导弹不参与打击任务;
2)设sgl=sg,对sgl去重得到sgl′=[1,2,3,4],根据P1和T1的位置以及sgl′,通过深度优先搜索获得sgl″=[1,2,3],再使用Dijkstra算法获得第1枚导弹的制导序列MG1=[1,3];
3)从sg中将1和3均删除一次,更新制导站序列为sg=[2,4,1,2,3,4];
4)根据P2和T2的位置以及sg,使用DFS算法和Dijkstra算法,获得MG2=[1,2,4];
5)由于P3携带的导弹不参与打击任务,故解码结束,得到PT和MG分别为
根据PT和MG计算f1和f2。
可以看出,本文研究设计的编码与解码方式建立了从st和sg到PT和MG的映射,后续通过遗传算法的选择、交叉、变异等操作,实现对st和sg的优化,进而实现对WTA方案及导弹制导序列的优化。
2.2 选择、交叉与变异
2.2.1 选择算子
选择算子采用二元锦标赛选择法[24]。在选择之前已对种群进行了非支配排序与拥挤距离计算。对于待选择的两个个体,选择Pareto等级较小的个体进入新种群;若Pareto等级相同,则选择拥挤距离较大的个体进入新种群;若拥挤距离也相同,则随机选择一个个体进入新种群。
2.2.2 交叉算子
设计交叉算子基本步骤如下所示(其中对sg的交叉参考文献[19]):
1)设交叉概率为pc(0≤pc≤1),待交叉的两个个体的染色体分别为st1和sg1、st2和sg2;
2)生成随机数0≤r≤1,若r>pc则两个体不进行交叉,否则交叉继续进行;
3)st1与st2进行交叉,生成随机整数i和j满足1≤i 4)sg1与sg2进行交叉,生成随机整数i和j满足1≤i 5)在sg2中寻找s1中的所有基因,并记录基因相对位置为s1′,在sg1中寻找s2中的所有基因,并记录基因相对位置为s2′(这里对同一制导序列中多次出现的相同制导站进行严格区分,确保序列中各基因的唯一性); 6)在sg1中用s1′替换s1,在sg2中用s2′替换s2,得到两条新的染色体sg1′和sg2′。 这里给出st与sg的交叉示例: ①假设st1=[1,2,2,3],st2=[3,1,1,2],交叉位置为第1位和第2位,首先交换st1和st2的第1位基因,交换后st1不满足目标1的毁伤次数约束(无导弹攻击目标1,必然违反目标最小毁伤概率约束),故两基因再次交换;然后交换st1和st2的第2位基因,不违反目标毁伤次数约束;交叉后的基因序列为st1′=[1,1,2,3]、st2′=[3,2,1,2]。 ②假设sg1=[1,2,3,4,5,6]、sg2=[1,3,5,2,4,6],若选取sg1中的片段s1=[2,3,4],则s1′=[3,2,4](因为在sg2中,基因2、3、4的相对位置为3-2-4),即sg1变为sg1′=[1,3,2,4,5,6],对sg2执行类似的操作。 2.2.3 变异算子 设计变异算子基本步骤如下所示(其中对sg的变异参考文献[19]): 1)设变异概率为pmu(0≤pmu≤1),待变异个体的两条染色体为st和sg; 2)生成随机数0≤r≤1,若r>pmu则该个体不进行变异,否则变异继续进行; 3)生成随机整数1≤i≤sum(PM),设st的第i位基因为n0,生成随机整数0≤n1≤N,用n1替换n0; 4)若n0≠0,且fnum(n0,st)<1,则随机选择一位st中值为0的基因(非第i位基因),将其值变为n0;若n1≠0,且fnum(n1,st)>dnm,则随机选择一位st中值为n1的基因(非第i位基因),将其值变为0;得到新的染色体st′; 5)随机选取sg中的某一片段s,将s随机打乱为s′,用s′替换s,得到新的染色体sg′。 这里给出st和sg的变异示例: ①假设st=[2,1,1,1,0,3],变异位置为第1位,st的第1位基因为n0=2,生成随机数n1=1,则st变为st=[1,1,1,1,0,3];判断攻击目标2的导弹数量小于1,需要将st的第5位基因由0变为2;假设dnm=3,则判断攻击目标1的导弹数量超过目标最大毁伤次数,需要将st的第2、3、4位基因中的一位由1变为0;最终得到新的染色体st′。 ②假设sg=[1,2,3,2,1,3],选取s=[2,3,2],则s′的可能取值为[2,2,3]、[2,3,2]、[3,2,2],用s′替换s得到新的染色体sg′。 将本文研究设计的交叉算子和变异算子作用于原本可行的个体(即解码结果不违反约束),操作后的个体解码结果必然满足1.2.3节的约束1、2、3、6,减少非可行解的产生。对于违反约束4或5的个体(即目标毁伤概率达不到最小毁伤概率,或找不到可行的制导序列),通过选择操作进行淘汰。 多种群NSGA-Ⅱ设置多个子种群,各子种群采用不同的控制参数,在迭代进化的过程中,通过移民算子,将各子种群中较为优秀的个体加入其它子种群,实现各子种群的协同进化,有利于克服传统遗传算法的算法早熟问题。 本文研究设计多种群NSGA-Ⅱ的子种群数量为nGA,各子种群规模均为nscale,迭代次数均为nev,第i个子种群的初始交叉概率为pc0i,最终交叉概率为pc1i,初始变异概率为pmu0i,最终变异概率为pmu1i,第i个种群在第j轮迭代中的交叉概率为pci,j,变异概率为pmui,j,计算公式为 (16) 在每一代进化中,各子种群均完成精英保留操作之后,进行移民操作,步骤如下: 1)对于每个子种群,选出所有Pareto等级为1的个体,目标函数值相同的多个个体只保留一个,获得各子种群的移民个体; 2)将第i个子种群的所有移民个体复制添加至第i+1个子种群(i=1,2,…,nGA-1),第nGA个子种群的所有移民个体复制添加至第1个子种群; 3)各子种群重新进行非支配排序、拥挤距离计算和精英保留。 决策者根据任务需求或自身偏好,从最终种群中选择某一个体,解码获得WTA方案与接力制导方案,作为最终方案。 DSMPNSGA-Ⅱ流程如图3所示。 图3 DSMPNSGA-Ⅱ流程图 具体流程如下: 1)参数与种群初始化,初始化参数包括攻击机、目标、制导站、导弹参数及遗传算法相关参数,种群初始化随机生成各子种群各个体的染色体基因序列,并解码计算目标函数; 2)各子种群进行非支配排序、拥挤距离计算、选择、交叉、变异、精英保留等操作; 3)子种群进行移民操作; 4)重复步骤2和步骤3,直到达到最大迭代次数; 5)将各子种群合并,并进行非支配排序; 6)从非支配个体中选择某一个体,解码获得最终WTA与制导序列结果; 7)输出最终方案。 为了验证本文提出的DSMPNSGA-Ⅱ求解空地多目标攻击WTA与制导序列优化问题的有效性,在Intel(R) Core(TM) i9-10900K 3.7 GHz CPU、16.0 GB RAM、Windows 7实验平台上,在Python 3.6实验环境下进行仿真计算。 作战区域东西距离为400 km,南北距离为200 km;攻击机数量M为10;目标数量N为5,目标最小毁伤概率dpm为0.6,最大毁伤次数dnm为3,各目标价值系数v1~v5分别为0.2、0.1、0.3、0.25、0.15;制导站数量K为25,制导半径RG为60 km,制导能力CG为3。各攻击机位置、目标位置和制导站位置如表1所示。 表1 攻击机、目标、制导站位置 空地导弹类型数量H为3,导弹数量为25,攻击机导弹配置矩阵PM如下: 导弹杀伤概率矩阵MT如下: 作战场景如图4所示,图4展示了本算例中各攻击机、目标、制导站的位置与编号,以及各制导站的制导区域。 图4 算例作战场景示意图 遗传算法参数为:子种群数量nGA为3,种群规模nscale为50,迭代次数nev为30,3个种群的初始交叉概率分别为0.5、0.8、0.5,最终交叉概率分别为0.1、0.3、0.1,初始变异概率分别为0.1、0.1、0.3,最终变异概率分别为0.02、0.02、0.1。 经过仿真计算,得到10种非支配的WTA与制导序列结果,各结果的目标综合生存概率f1、总用弹量f2如表2所示。 表2 算例结果 在表2中,完成空地多目标攻击任务所需的最少用弹量为5,此时每个目标仅被一枚空地导弹攻击,满足各目标最小毁伤次数与最小毁伤概率约束;随着用弹量的不断增加,目标的综合生存概率不断减小,即综合毁伤概率不断增大;最大用弹量为14,受到目标最大毁伤次数与制导站制导能力的限制,用弹量无法继续增加,综合毁伤概率无法继续提升。 决策者根据任务需求或自身偏好,从表2中选择一种方案作为最终方案。例如打击任务要求目标的综合毁伤概率达到0.93,即目标综合生存概率不得超过0.07,则从结果7~10中选择用弹量最少的方案,即将结果7对应的WTA方案与接力制导方案作为最终方案,方案详情如表3所示。 表3 最终方案详情 绘制最终WTA与接力制导方案如图5所示,图5(a)~图5(e)展示了参与打击任务的各导弹航迹以及为导弹进行接力制导的制导站,各导弹航迹使用A*算法[25]规划得到。其中对于图5(d),打击目标4的空地导弹有3枚,而图中只显示了2条导弹轨迹,原因是其中两枚导弹均由6号攻击机发射,导弹轨迹重合。 图5 最终WTA与接力制导方案 为充分展示DSMPNSGA-Ⅱ的优化效果,将算法运行20次,绘制平均f1、f2的变化曲线如图6所示。平均目标函数值计算方法为:记录每次运行的每一轮迭代中,种群所有个体f1、f2的平均值,并计算相同迭代次数下,各目标函数平均值对算法运行次数的平均值。 图6 平均目标函数值变化曲线 从图6可以看出:在迭代初期,f1与f2均呈下降趋势,故DSMPNSGA-Ⅱ能够有效实现空地多目标攻击WTA与制导序列的优化;而在迭代后期,两目标函数值均出现波动,平均总用弹量甚至略有上升,原因是两个目标函数存在耦合,不会同时达到最小,并且迭代后期,很多个体已成为非支配最优个体,继续迭代只会将一种非支配最优个体转化为另一种非支配最优个体,若出现大量个体向f1减小、f2增加方向转化的情况,则平均用弹量上升。 对本研究提出的DSMPNSGA-Ⅱ,与单种群NSGA-Ⅱ以及文献[26]提出的多目标离散粒子群优化(MODPSO)算法分别进行对比,对比算法参数设置如下: 1)单种群NSGA-Ⅱ:种群规模为150(与多种群NSGA-Ⅱ的子种群规模之和相同),初始交叉概率为0.5,最终交叉概率为0.1,初始变异概率为0.1,最终变异概率为0.02; 2) MODPSO算法:种群规模为150,初始变异概率为0.1,最终变异概率为0.02,Pareto外部档案最大规模为50。 通过3个算例进行对比,各算例的主要区别为制导站的数量K与制导能力CG,各算例参数设置如下: 1)算例1:算例参数与3.1节所述参数相同; 2)算例2:CG为2,其余参数与算例1相同; 3)算例3:K为17(从图4中删去编号为2、4、6、8、16、17、23、24的制导站),其余参数与算例1相同。 在每个算例中,3种算法均运行20次,算法性能的评价指标如下: 1)平均计算时长:算法每次运行时长的平均值,反映算法的计算速度; 2)平均非支配解数量:算法每次运行所得非支配解种类数的平均值,反映算法优化结果的多样性; 3)平均非支配比率:将不同算法的非支配解合并,并进行非支配排序,获得总非支配解集,各算法原非支配解在总非支配解集中所占比例即为各算法的非支配比率[27],该指标反映算法所得非支配解的质量。 各算例对应的算法对比结果如表4~表6所示。 表4 算例1算法对比结果 表5 算例2算法对比结果 表6 算例3算法对比结果 从表4~表6可以看出,对于3种多目标优化算法,在算例1中,平均计算时长更长、平均非支配解数量更多。与算例1相比,算例2降低了制导站的制导能力,算例3减少了制导站的数量,二者都会造成可行WTA与接力制导方案数量的下降,即平均非支配解数量的下降,但也使得算法搜索空间变小、染色体长度缩短,算法操作得以简化,因此算法速度有所提升,即平均计算时长下降。 3种算法对比结果如下: 1)计算速度方面,DSMPNSGA-Ⅱ略慢于单种群NSGA-Ⅱ(平均计算时长在算例1~算例3中分别落后1.61 s、1.08 s、0.55 s),而明显快于MODPSO算法(平均计算时长在算例1~3中分别提升79.01 s、54.37 s、48.10 s)。算法的计算量主要在对个体的解码并计算目标函数值上,一旦个体基因发生了改变,则需要重新计算目标函数值。DSMPNSGA-Ⅱ的第2和第3种群分别拥有更大的交叉概率与变异概率,与单种群NSGA-Ⅱ相比,个体交叉或变异次数更多,因此DSMPNSGA-Ⅱ的计算速度略慢于单种群NSGA-Ⅱ;而MODPSO算法的每个个体在每轮迭代中都会进行交叉操作,并重新解码计算目标函数值,因此计算速度最慢; 2)优化结果多样性方面,DSMPNSGA-Ⅱ显著优于单种群NSGA-Ⅱ(平均非支配解数量在算例1~3中分别提升1.05、0.60、0.85),略优于MODPSO算法(平均非支配解数量在算例1~3中分别提升0.45、0.20、0.05)。可以看出,采用了多种群策略的DSMPNSGA-Ⅱ能够获得更为多样的WTA与接力制导方案。 3)非支配解质量方面,与单种群NSGA-Ⅱ和MODPSO算法相比,DSMPNSGA-Ⅱ的非支配比率更高(在算例1~3中的平均非支配比率比单种群NSGA-Ⅱ分别高26.00%、30.94%、36.78%,比MODPSO算法分别高12.24%、4.57%、6.05%),因此DSMPNSGA-Ⅱ的求解质量更高。 综上,根据不同制导站数量与制导能力下的算例仿真与算法对比结果,DSMPNSGA-Ⅱ在计算速度上略慢于单种群NSGA-Ⅱ,但明显快于MODPSO算法;在优化结果多样性以及求解质量方面,均优于单种群NSGA-Ⅱ和MODPSO算法。在优化问题规模较大、可行WTA与接力制导方案数量较多时,DSMPNSGA-Ⅱ的优势更为明显。 本文对远距离空地多目标攻击中亟需解决的WTA与空地导弹接力制导规划问题进行了研究。得出以下主要结论: 1)构建远距离空地多目标攻击作战场景,并建立多目标、多约束WTA与制导序列优化模型,以目标综合生存概率最小和总用弹量最少为优化目标,综合考虑攻击机导弹配置、导弹毁伤能力、目标毁伤要求、制导站制导性能等约束条件。 2)提出基于双序列编码的多种群NSGA-Ⅱ,对WTA与制导序列优化模型进行求解。建立WTA序列和制导站序列到WTA方案与接力制导方案的映射,通过DFS-DJ搜索方法、改进的染色体交叉与变异操作、多种群策略等,提升算法性能。 3)通过算例仿真,验证了DSMPNSGA-Ⅱ求解WTA与制导序列优化问题的有效性,并将DSMPNSGA-Ⅱ与单种群NSGA-Ⅱ以及MODPSO算法进行比较,验证了DSMPNSGA-Ⅱ在计算速度、优化结果多样性、求解质量等方面的优越性。 本文研究有助于提升远距离空地多目标攻击的成功率、减少资源消耗。未来研究拟考虑更为复杂的战场环境,加入地形、禁飞区、敌方威胁等约束条件,并提升算法计算速度。2.3 多种群NSGA-Ⅱ
2.4 最终方案选择
2.5 算法流程

3 仿真与算例分析
3.1 参数说明


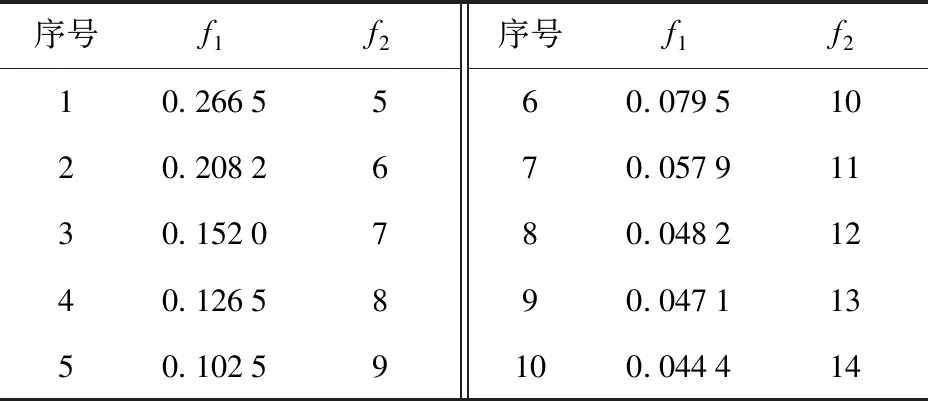
3.2 仿真结果



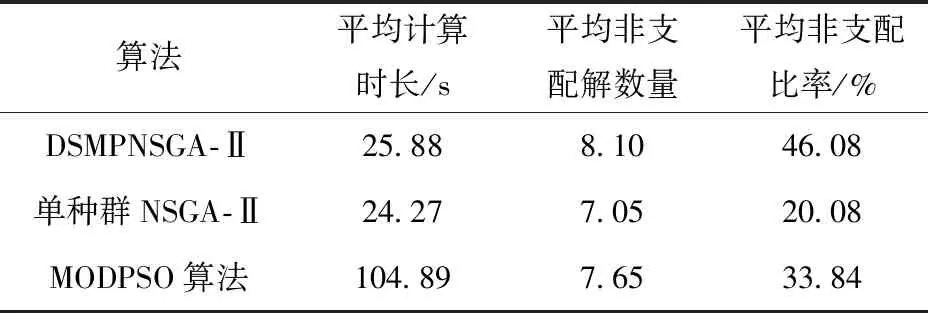
3.3 算法对比
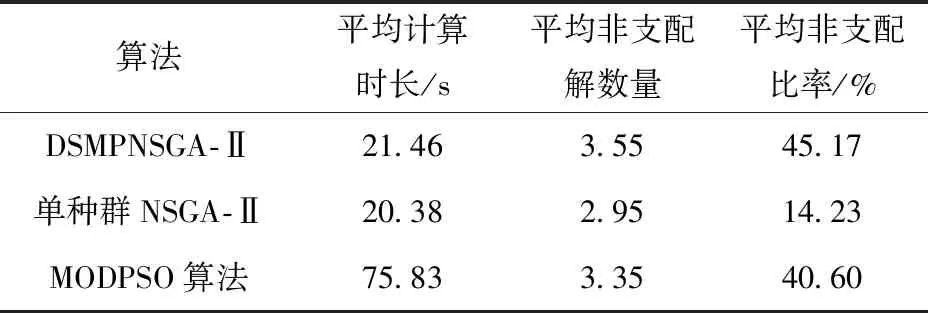
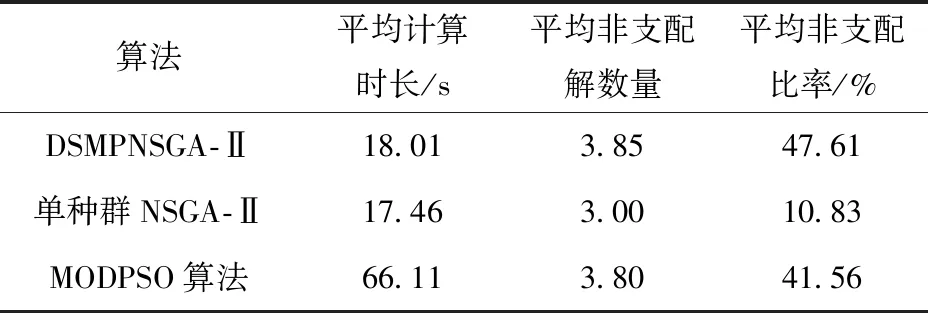
4 结论
