风标式攻角传感器在超声速飞行运载火箭中的应用研究

高 波，姚 瑶，杨学军，蒋 平

(北京宇航系统工程研究所，北京 100074)

0 引言

攻角作为一种重要的飞行参数，其高精度的测量显得尤为必要[1-2]。20世纪60年代初期,国外就有成功运用攻角传感器测量攻角信息的报道[3]。

攻角传感器主要分为气动式和机械式两大类，气动式是通过压力信息解算飞行攻角，例如压差比传感器，而机械式则利用探头转动获得飞行攻角，例如风标传感器[4]。风标式攻角传感器主要由风标、转轴以及角度变换器构成。如果飞行器轴线相对于气流的方向发生改变，则风标的楔形截面对称线将不平行于气流的方向，此时作用于风标上下两个面上的气动力不再相等，形成一个转矩，迫使风标绕轴转动，直至其截面的对称线重新平行于气流的方向为止。美国A4舰载攻击机、B1轰炸机、F5战斗机、军用运输机以及许多民航客机都安装了风标式攻角传感器[5]。

20世纪60年代，美国国家航空航天局提出嵌入式大气数据传感系统，以期通过压力传感器阵列测量获得飞行参数[6-10]。1981年，Thomas等通过大量的风洞以及飞行试验对安装于飞机机翼前缘的机械式攻角传感器进行修正，并得出当攻角较大时侧滑角影响不可忽略的结论[11]。Andy等运用数值仿真分析了飞机舱门局部流场对风标传感器的影响，认为传感器高度与边界层高度相当，舱门局部流动影响较小[12]。在国内，1994年，汤黄华[13]通过对压差式攻角传感器的理论分析，给出机身侧曲线上压力系数Cp=0位置处的安装建议。2015年，赵克良等[14]针对飞机上风标式攻角传感器进行了数值研究，得出其理想安装区域为轴向48%～100%机头最大宽度线上的结论。

目前，对于攻角传感器的研究主要集中于各类飞机上的应用。而较大风攻角引起的箭体的载荷设计困难愈加凸显，使得实现箭体的实时攻角控制方案需求愈加紧迫。常见的测量箭体飞行姿态的方法有陀螺仪、重力加速表、太阳方位角传感器等[15-17]。但攻角传感器在箭体设计中的应用鲜有研究。攻角传感器的探测攻角与实际飞行攻角的关系(探测特性)，受安装位置、飞行流场等因素的影响。对于飞机而言，其外形复杂，各型飞机间亦存在较大差别，因此通常其探测特性只能通过大量的飞行试验或风洞试验获得。而对于火箭而言，其外形简单，大多为旋成体的柱段或锥段，因此其探测特性必然存在一定的规律性，运用数值手段结合理论分析获得其探测特性的规律，可以有效节省试验经费及周期，为攻角传感器在火箭上的工程应用提供支撑。

本文从3个方面研究风标攻角传感器在运载火箭设计中的应用问题：1)攻角传感器在超声速气流中的跟随响应特性；2)火箭绕流条件下，自由来流攻角与箭体当地攻角的对应关系；3)箭体当地攻角与攻角传感器输出攻角的解算关系。第一个问题决定风标式攻角传感器能否适应运载火箭的超声速飞行环境，后两个问题给出从攻角传感器测量输出攻角到真实飞行攻角转换的探测特性。文中所指攻角均不考虑弹性修正。

1 攻角传感器动态特性试验研究

为了获得某型攻角传感器的静态与跟随特性，进行了相应的风洞试验。模型采用侧窗安装方式，由螺钉安装于侧窗平台上并与侧窗转动机构相连，使得模型与侧窗同步改变攻角，如图1所示。

图1 攻角传感器风洞安装图Fig.1 Angle of attack sensor in wind tunnel

试验通过测量风标式传感器输出电压转换得到其当地攻角，并与风洞攻角机构(窗盘)输出攻角对比。信号采集方式分为连续采集,攻角机构采用一定角速率(试验中取10(°)/s)连续变化，同时动态采集系统采用一定频率(试验中取5kHz)进行输出电压的采集。

图2为攻角传感器的动态跟随特性，黑点为来流实际攻角，红点为传感器输出攻角，其中有斜率部分为攻角连续变化时间段。可以看出，攻角传感器测量数据与风洞机构给定攻角数据一致性较好，能够较为准确地动态捕捉来流攻角，为后续实际工程应用提供支撑。

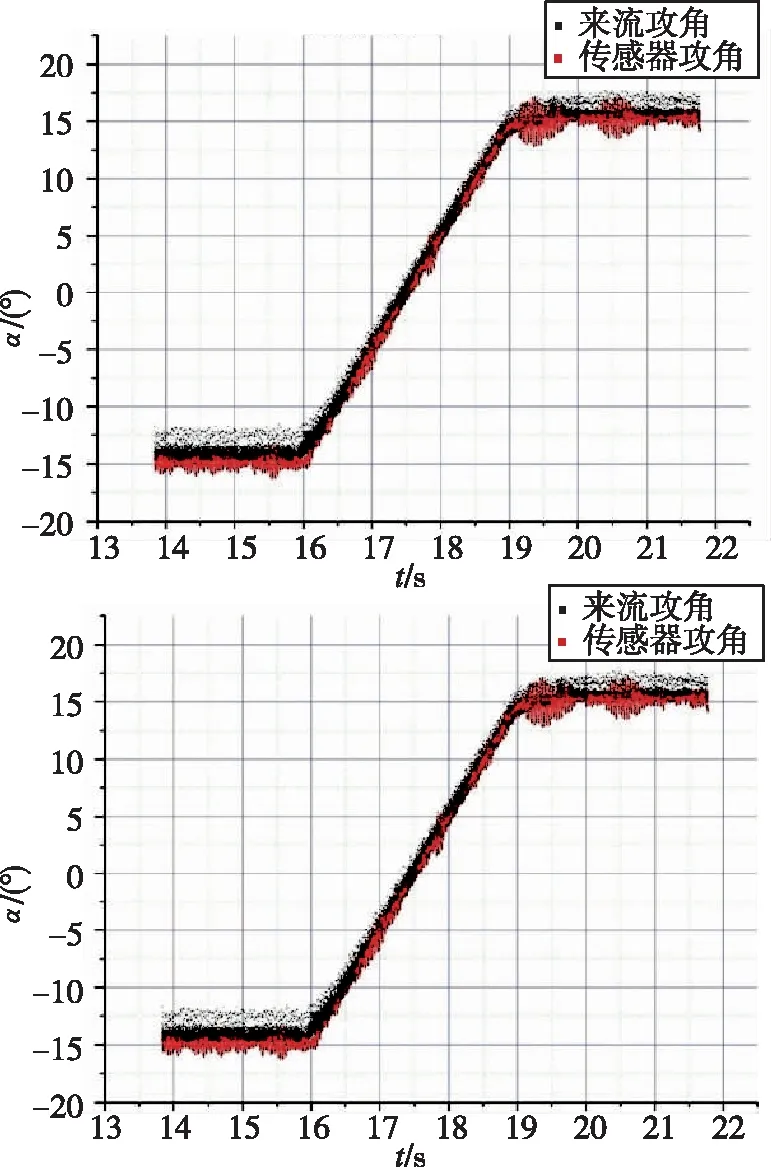
图2 攻角传感器的动态跟随特性Fig.2 Dynamic following characteristics of the angle of attack sensor(Ma=3.02)

2 来流攻角与当地攻角的关系

当地攻角定义为当地速度与箭体坐标系的夹角。不考虑箭体绕流的影响，由于流动贴附在箭体表面，在攻角平面内当地攻角不反映来流攻角信息，柱段处当地攻角为0°，锥段处为锥角本身；在垂直于攻角的平面内当地攻角等于来流攻角。考虑箭体绕流的影响，当地攻角与来流攻角存在一定差异，该差异与气动外形及飞行工况相关。本节针对某运载火箭气动外形，以Ma=2.5为分析工况，研究典型锥段剖面和柱段剖面的当地攻角与来流攻角的关系。如图3所示，取5个典型剖面进行分析：锥段一(点1)、柱段一(点2)、锥段二(点3)、柱段二(点4)以及柱段三(点5)。

图4给出了一些典型位置处的速度型。锥段一激波层与边界层距离很近，不容易辨识出边界层厚度。柱段一和锥段二的边界层厚度为70mm～80mm，柱段二边界层厚度约为100mm，柱段三边界层厚度为130mm～140mm。风标式攻角传感器的安装高度约为80mm，与边界层厚度相当，需要分析边界层内的当地攻角。边界层厚度与当地雷诺数直接相关，与攻角无关。

图3 Ma=2.5, α=0°对称面马赫数云图Fig.3 Mach contour under Ma=2.5, α=0°

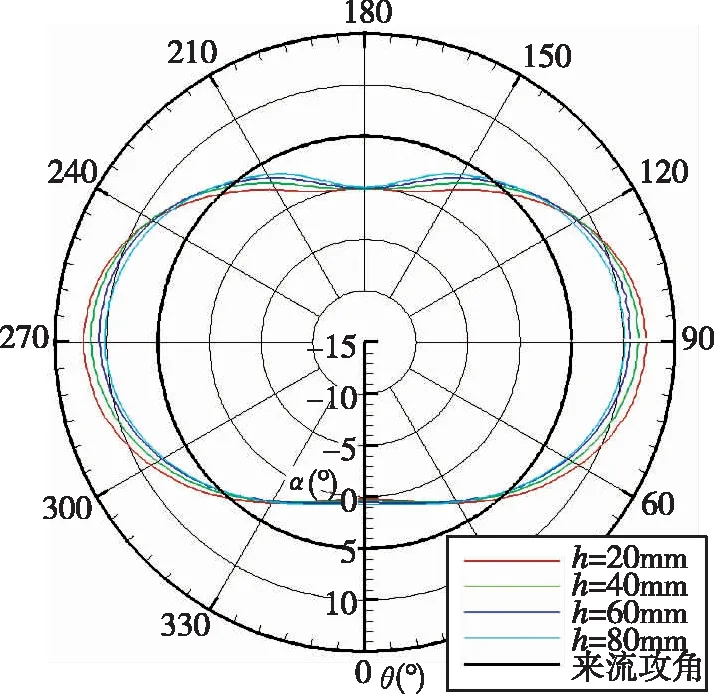
图5～图6给出了极坐标系下各典型位置处当地攻角与来流攻角的关系。根据箭体表征习惯，从上游看，横截面底部为Ⅰ象限，逆时针相隔90°依次为Ⅱ、Ⅲ、Ⅳ象限，由此绘制柱坐标下曲线。黑色粗圆曲线表征来流攻角α0，彩色曲线表征距离壁面不同高度h(20mm、40mm、60mm、80mm)处的当地攻角。不同工况下同一截面上的当地攻角分布规律基本一致，并且距离壁面的高度影响较小。

(a)点1处速度剖面

(b)点1近壁处速度剖面

(c)点2处速度剖面

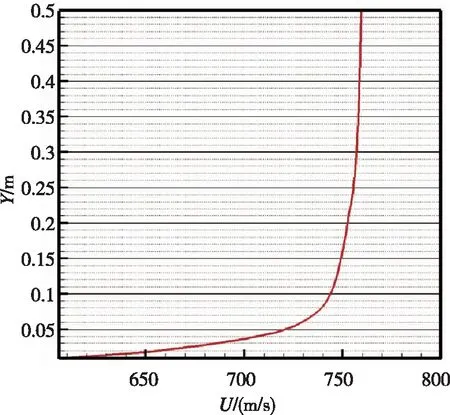
(d)点2近壁处速度剖面

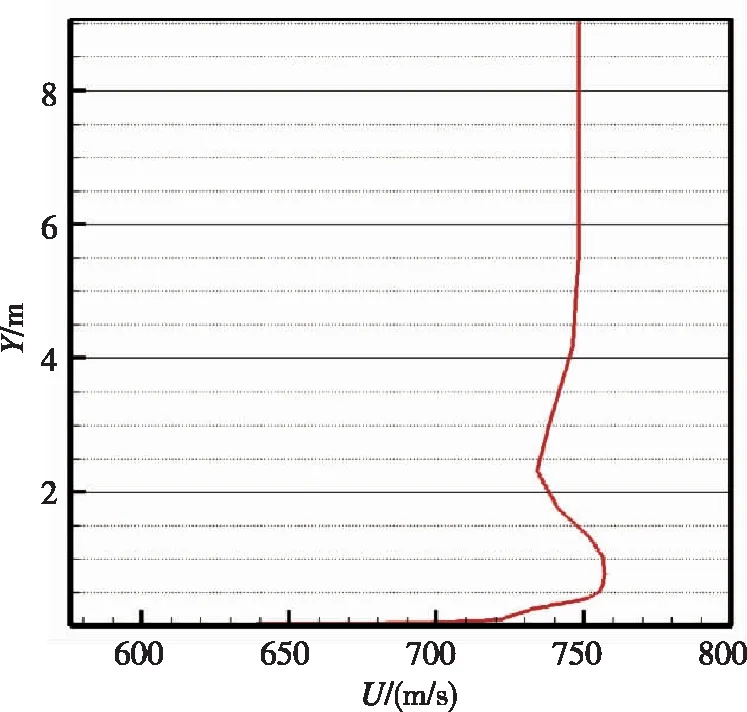
(e)点3处速度剖面

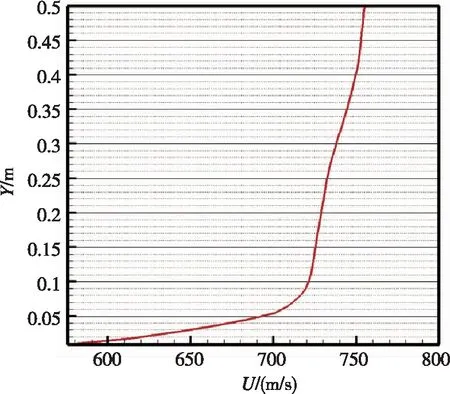
(f)点3近壁处速度剖面

(g)点4处速度剖面

(h)点4近壁处速度剖面

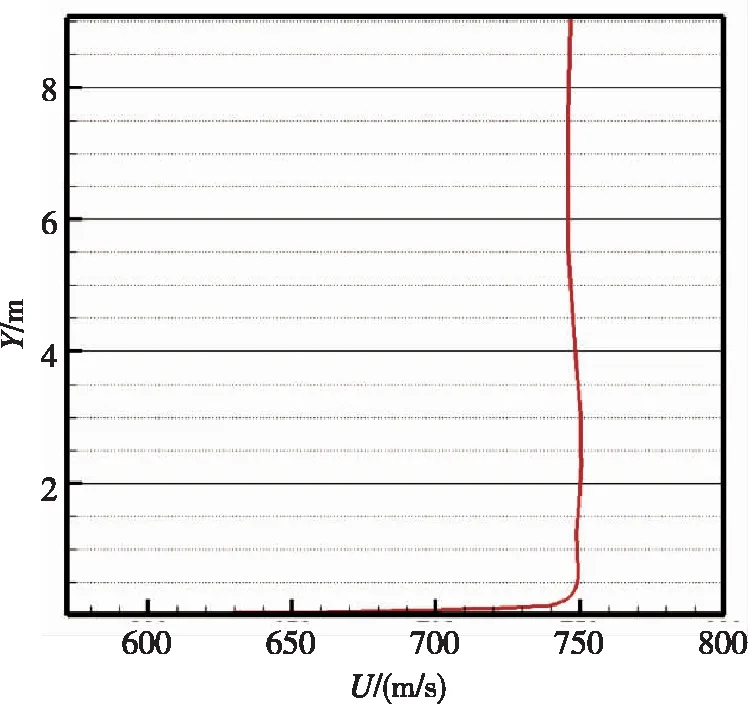
(i)点5处速度剖面

(j)点5近壁处速度剖面

(a)锥段一(点1)

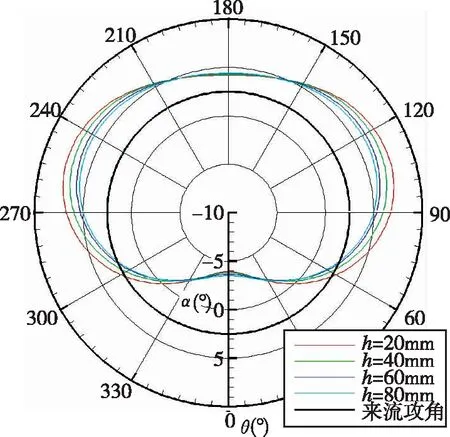
(b)锥段二(点3)

(c)柱段一(点4)

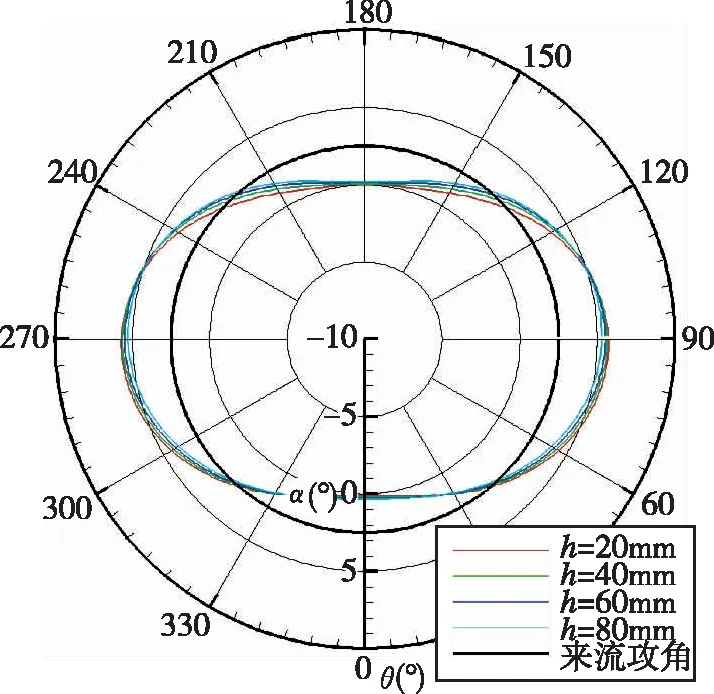
(d)柱段二(点5)

(a)锥段一(点1)

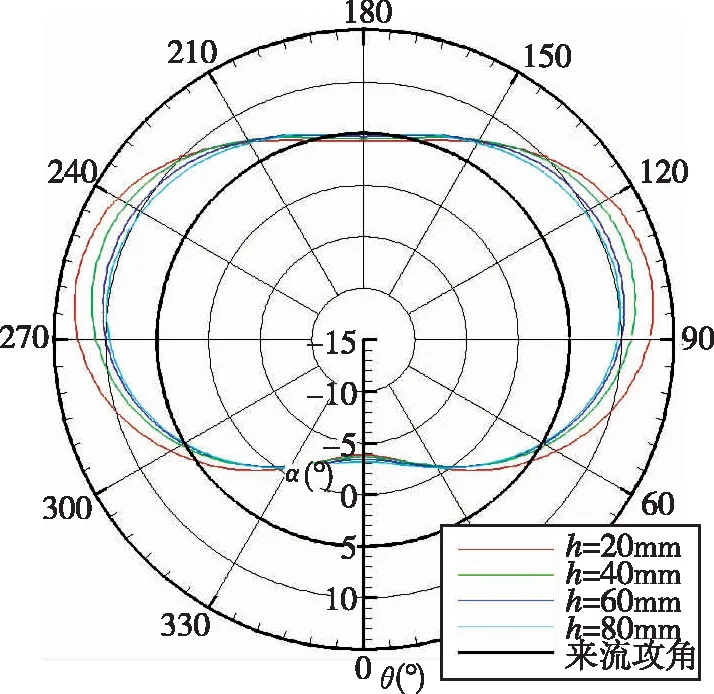
(b)锥段二(点3)

(c)柱段一(点4)

(d)柱段二(点5)

在攻角平面(0°, 180°)内，柱段处的当地攻角为0°，锥段处的当地攻角为锥角，与不考虑绕流影响的分析一致，这是由于在一定攻角范围内，箭体表面没有发生分离，流体仍然贴体流动，攻角平面内不反应攻角信息。在垂直于攻角的平面(90°, 270°)内，受绕流流场影响，当地攻角大于来流攻角。在柱段，两平面夹角的中心位置(45°、135°、225°、315°)处，当地攻角大致与来流攻角相当；在锥段，扣除锥角可以获得和柱段一致的规律。因此，应将攻角传感器安装在这几个位置，不受锥段或是柱段的影响，可以比较真实地捕获来流攻角。

3 探测攻角与当地攻角的解算关系

攻角传感器的安装位置(当地箭体锥角、周向安装角)，影响着当地攻角与传感器输出攻角(探测攻角)的解算关系。当地攻角与探测攻角的关系可由坐标变换获得，对于规则旋成体外形，需要考虑柱段和锥段两种形状。

对于柱段，设速度坐标系为OX1Y1Z1，箭体坐标系为OX2Y2Z2，攻角传感器当地坐标系OX3Y3Z3，如图7所示。假设攻角传感器周向安装角为θ，当地攻角为α，当地侧滑角为β，探测攻角为α′。

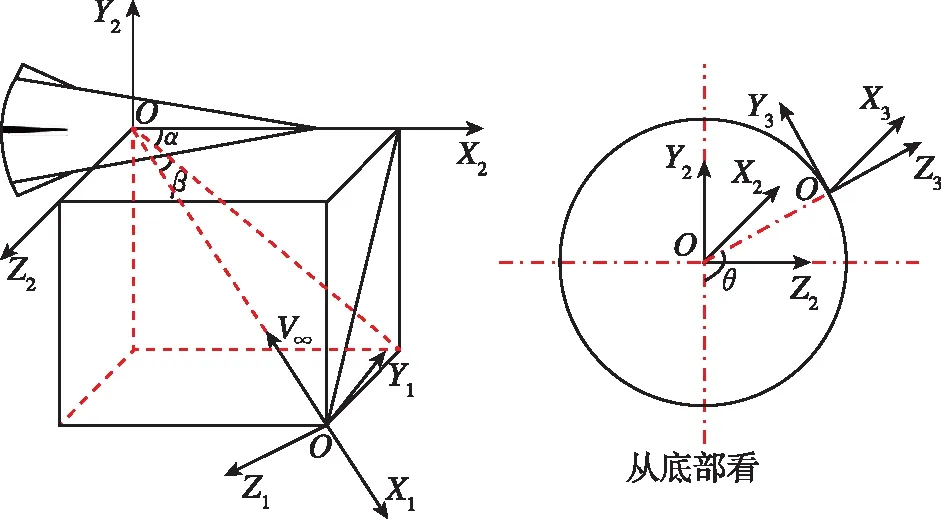
图7 各坐标系转换关系示意图Fig.7 Schematic of coordinates transformation

从速度坐标系到箭体坐标系的基矢量变换方程描述为：首选从速度系OX1Y1Z1下绕Y1轴旋转β角得到OX12Y1Z2，然后再绕Z2轴旋转角α得到箭体坐标系OX2Y2Z2。基矢量变换方程为

(1)

同理，从箭体坐标系到当地坐标系的基矢量变换方程为

(2)

以上两式可得速度坐标系到当地坐标系的变换矩阵为

(3)

式中，A=-sinαcosβsinθ-sinβcosθ;

B=-sinαcosβcosθ+ sinβsinθ;

C=sinαsinβsinθ-cosβcosθ;

D=sinαsinβcosθ+ cosβsinθ。

速度坐标系下的速度矢量为[U,0,0]′，当地坐标系下的速度矢量为[u3,v3,w3]′，两者关系为

(4)

探测攻角α′与当地坐标系速度关系为

(5)

对于β=0°，在θ=0°、180°位置处，tanα′=0→α′=0，探测攻角为0，无法感应攻角；在θ=90°位置处，tanα′=tanα→α′=α；在θ=270°位置处，tanα′=-tanα→α′=-α，探测攻角与当地攻角一致。

实际使用中，已知的是探测攻角α′，以及其周向安装位置角θ。在两个不同周向位置各安装一个攻角传感器时，有

(6)

消除β后，可得

(7)

进一步整理有

(8)

理论上最少使用两个攻角传感器即可确定攻角和侧滑角，但实际上受流场本身的影响，不能辨识侧滑角对当地攻角的影响。因此，在4个象限分别布置一个攻角传感器比较理想，可以尽量减小攻角与侧滑角辨识过程中的交联干扰。

对于锥段，设锥角为φ，需要进一步将当地坐标系OX3Y3Z3绕Y3轴旋转φ

(9)

因此，新的变换矩阵为

(10)

式(5)变为

(11)

式中，E=sinφsinαcosβcosθ, 同样可以整理得到

(12)

式中，F=tanα2′ cosφ(cosθ1-tanα1′ sinφsinθ1);G=tanα1′ cosφ(cosθ2-tanα2′ sinφsinθ2);H=(tanα2′-tanα1′) sinφcos(θ1-θ2);I=tanα1′ tanα2′ sin2φcos(θ1+θ2);J=sin(θ1-θ2) 。

式(11)为考虑锥角情况下，探测攻角和侧滑角与当地攻角的解算关系，结合第2节来流攻角与当地攻角的关系即可获得探测攻角与来流攻角之间的关系，即攻角传感器的探测特性。考虑α0=5°,β=0°情况，锥段及柱段探测特性如图8所示。

在柱段(φ=0°)，攻角平面内探测攻角为0°，垂直于攻角平面内探测攻角等于当地攻角、大于来流攻角，在两平面夹角的中心位置(45°、135°、225°、315°)处，通过探测攻角解算出的当地攻角可以较为真实地反应来流攻角；在锥段，扣除锥角可以得到与柱段一致的规律。

(a)锥段一(点1)

(b)柱段一(点4)图8 不同锥角情况下攻角传感器输出攻角Fig.8 Detected angle of attack

4 结论

本文首先基于风洞试验验证了某型风标式攻角传感器良好的静态以及跟随特性。针对箭体常采用的规则旋成体——锥、柱，运用数值仿真分析当地攻角与来流攻角的关系、不同位置及高度的影响。同一位置处不同高度当地攻角的变化较小，而同一截面不同周向位置上的影响则较大。在攻角平面内当地攻角不反映来流攻角信息，在垂直于攻角的平面内，受绕流流场影响，当地攻角大于来流攻角。在两平面夹角的中心位置处，对于柱段，当地攻角大致与来流攻角相当；对于锥段，扣除锥角可以获得和柱段一致的规律。因此应将攻角传感器安装在这几个位置，可以比较真实地捕获来流攻角。

然后,运用数学分析解算出柱段及锥段的探测攻角与当地攻角、侧滑角的变换关系。理论上最少使用两个攻角传感器即可确定攻角和侧滑角，但实际上受流场本身的影响，不能辨识侧滑角对当地攻角的影响。因此，在4个象限的中线上分别布置一个攻角传感器比较理想，可以尽量减小攻角与侧滑角辨识过程中的交联干扰。