学科育人导向下问题驱动式单元复习课教学实践与思考
2023-07-28熊俊


[摘 要] “如何发挥学科育人价值”是教育工作者当前迫切需要思考的问题,也是对教育本真的不懈追求. 现结合一节“圆”单元复习课的问题设计和课堂教学实例,探究如何通过问题驱动式课堂教学创设新的复习课生态,让学生在数学课堂中获得生长,从而达到数学学科育人的目的.
[关键词] 学科育人;问题驱动;单元复习课
作者简介:熊俊(1988—),硕士研究生,中学一级教师,从事中学数学教学与研究工作,曾获南京市初中数学优质课大赛一等奖,主持南京市教育科学规划第十二期个人课题“学科育人导向下问题驱动式教学模式在初中数学复习课教学中的实践研究”(Lc1010).
党的十八大报告把立德树人作为教育的根本任务,“学科育人”成为教育领域的热点问题,那么数学学科如何培养人呢?[1]在此背景下,笔者开展了“学科育人导向下问题驱动式初中数学复习课教学实践研究”的课题研究. 本文以苏科版九年级数学上册“圆”单元复习作为研究对象进行教学实践,拟简单呈现这节复习课的问题设计、教学实施和实践反思,与同人交流,以期得到更多、更好的复习课教学成果.
问题驱动式“圆”单元复习课的问题设计及教学实施
问题 在圆中画两条弦,你会有哪些发现?
【设计意图】
通过“在圆中画两条弦”这个问题,促发学生思考两条弦与圆的不同构图,促使学生运用分类思想分析解决问题. 在每一种构图的基础上进一步思考“有哪些发现”引发学生挖掘图形之间的关系,引导学生讨论知识之间的联系,驱动学生自主构建本章的知识体系. 相比于教师主导下的复习回顾,“在圆中画两条弦”的新问题可以激发学生的兴趣,一个切入口宽广的问题也会让每一个学生都能参与进来. 此外,该问题广度较宽,能够不断延伸,学力较强的学生可以利用充足的时间去思考、关联、转化,从两条弦的位置关系深入思考数量关系. 在此过程中,学生知识体系的建立和思维能力的生长不断螺旋上升.
【教学实施】
师:在圆中画两条弦,你会怎么画呢?试试看.
(学生开始画图)
师:画好后标记好点,观察图形,你有哪些发现?请写下来.
(学生展开思考,教师巡视、捕捉生成性资源)
师:画两条弦,你是怎么想的?
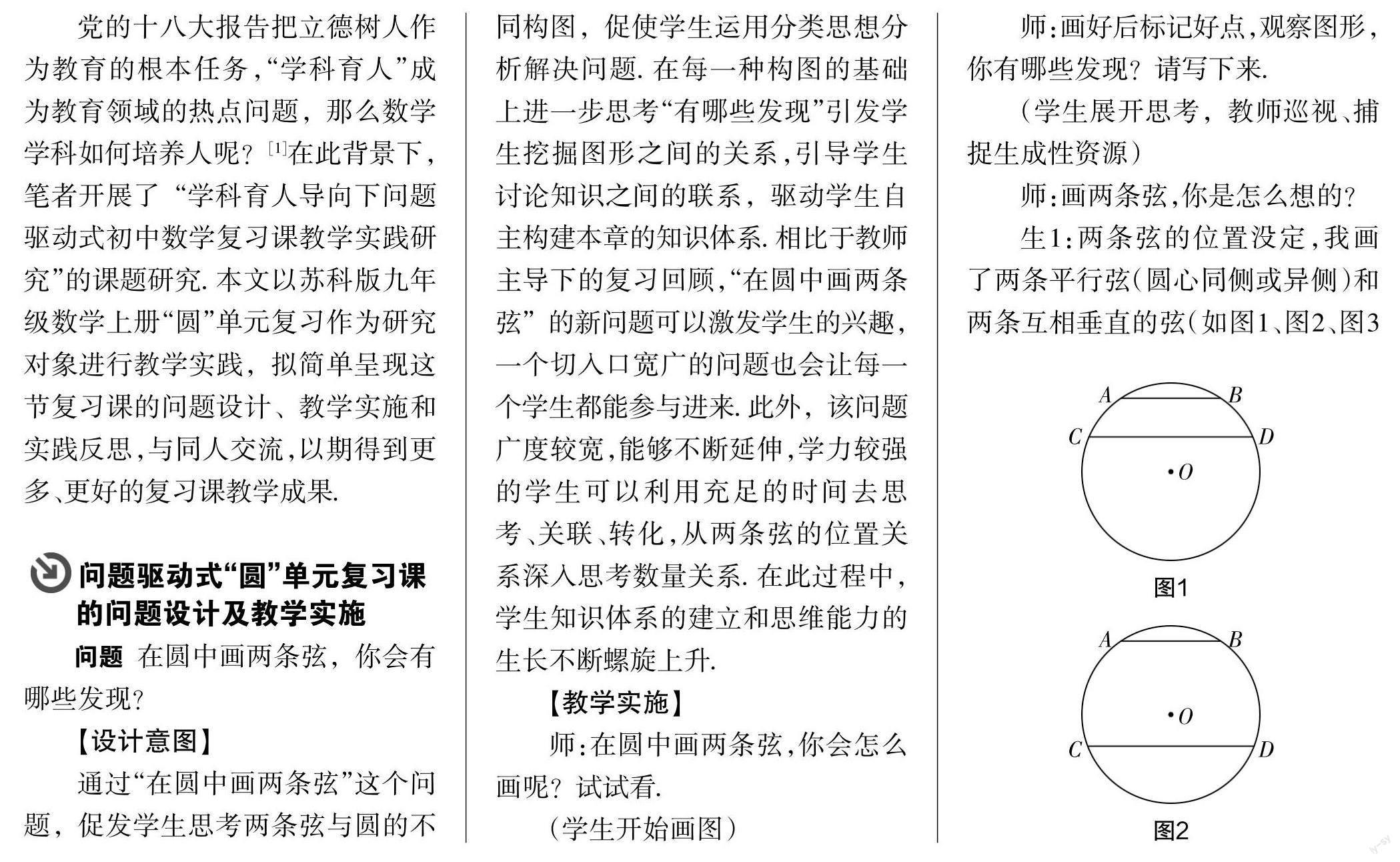
生1:两条弦的位置没定,我画了两条平行弦(圆心同侧或异侧)和两条互相垂直的弦(如图1、图2、图3所示).
师:有哪些发现?
生2:两条平行弦所夹的弧相等;(垂径定理)垂直于弦的直径平分弦且平分这条弦所对的两条弧.
师:你知道垂径定理和圆的什么属性有关吗?
生3:轴对称性,直径是圆的对称轴.
师:平行弦所夹弧相等又如何证明呢?
生4:根据图1,我们可以连接BC,因为AB∥CD,所以∠ABC=∠BCD,所以=.
师:由∠ABC=∠BCD得到=的依据是什么?
生5:我认为由∠ABC=∠BCD不能直接得到=,应根据“同弧所对的圆周角是圆心角的一半”先得到圆心角相等,然后由“三量关系定理”才能得到弧相等.
师:能具体说说“三量关系定理”吗?
生5:在同圆或等圆中,等弧、等弦、相等的圆心角可以互相转化.
师:“三量关系定理”和圆的什么属性有关呢?
生6:圆的旋转不变性.
师:异侧的情况可以类似地证明.
(此时教师完成板书1)
师:在圆中画两条弦,还有不同的画法吗?
生7:我画了两条特殊的相交弦,它们组成了一个圆周角,圆周角是圆心角的一半.
师:这是圆周角定理,还有补充吗?
生8:同弧或等弧所对的圆周角都相等. 比如,我们再画几个同弧所对的圆周角∠A1,∠A2,∠A3,因为都是圆心角∠O的一半,所以都相等.
师:若是同弦所对的圆周角还保持这样的特性吗?画一画.
生9:同弦所对的圆周角分为上、下两个,同侧的圆周角都相等,但异侧的圆周角是互补的关系.
师:大家看,在思考构图问题时,我们常常需要分类讨论.那么同弦所对的两侧的圆周角互补是如何得到的呢?
生10:圆内接四边形对角互补.
师:你能证明“圆内接四边形对角互补”吗?
生10:还是根据圆周角定理,将两个圆周角转化到圆心角正好拼成360°,圆周角是圆心角的一半,即180°.
(此时教师完成板书2)
师:还有其他想法吗?
生11:如果弦AB是直径,连接BC,AC,那么∠ACB是直角,因为直径所对的圆周角是直角.
师:特殊的弦对着特殊的圆周角. 反过来也成立,即90°的圆周角所对的弦是直径.
(此时教师完成板书3)
师:画两条弦,除了考虑位置关系还能想到什么呢?
生12:数量关系.
师:若是两条相等的弦呢?
生13:若是两条相等的平行弦,连接AC,BD,我们可以得到一个矩形.
师:大家想想如何证明.
生14:如图7所示,根据AB=CD得=,由AB∥CD得=,相加得到=,也就是半圆,于是∠C=∠B=90°. 同理可证∠CAB=∠CDB=90°. 于是ACDB为矩形.
师:若是两条等弦相交呢?又有什么发现?
生15:類似于等弦平行,如图8所示,可得=,于是∠CAB=∠ACD,根据等角对等边得到AP=CP,PB=PD.
生16:如图8所示,连接OA,OC,由OA=OC和AP=CP可以证明OP所在直线垂直平分AC和BD,是整个图形的对称轴.
生17:相互垂直是特殊的相交,前面的结论都成立.
师:大家再仔细看看,这里藏了“一线三垂直”的基本图形,但它们并不是全等哦(如图9所示).
师:如果把弦看作圆的内接线段,那么这条弦所在的直线与圆有什么关系呢?
生18:这条直线与圆相交.
师:直线与圆还有什么关系呢?
生19:根据圆心与直线的距离d和半径r来判断. 当d
(教师此时完成板书4)
师:在直线与圆的位置关系中,哪一种情况最特殊?具体说一说.
生20:相切最特殊. 若直线与圆相切,则圆心与切点连接的半径与直线垂直;若直線与圆相交的一点与圆心连接的半径与直线垂直,则圆与直线相切.
生21:过圆外一点P作圆的切线两条,且切线长相等.
师:在切线长定理的基本图形中,你还有哪些发现?
生22:OP是∠APB的平分线.
生23:OP垂直平分AB,由PA=PB,OA=OB,以及垂直平分线判定定理可证.
生24:再添一条切线,会出现三角形的内切圆,可以用等积法求内切圆的半径.
师:三角形与圆还有其他关系吗?
生25:还有内接三角形与外接圆.
师:不妨连接三个切点,☉O就成了△ABF的外接圆了. 内接三角形ABF的内角与谁有关?
生26:内接三角形的内角是外接圆的圆周角,所以∠AFB=∠AOB. 根据切线的性质定理得∠APB+∠AOB=180°,所以∠AFB= (180°-∠APB).
师:与圆有关的图形,最简单的是“点”,然后有直线、三角形、四边形、正多边形等. 几何图形之间的关系紧密,解决图形问题时要多关联相关图形. 比如三角形隐藏的外接圆.
(此时教师完成板书5)
师:至此,我们建立了圆内外相关元素之间的关联体系. 大家可以看到:图形万般变化皆归一个系统,问题不尽相同方法皆能统一.
例题 如图12所示,在△ABC中,AB=AC,以BC为直径的☉O交AB,AC分别于点D,E. 求证:DB=CE.
【设计意图】
在复习课章节知识体系建立完成的基础上,设计例题并借用本章知识解决. 本题要证明的是DB=CE,可以从不同视角入手:若定位为等弦,则可以关联转化到圆心角、等弧、圆周角等圆内部元素来思考;若定位为等线段,则可以联系到全等或等角对等边;若能想象到切线长,则可以挖掘隐圆条件. 通过对证明对象不同定位,让学生再一次亲历分类与转化,让数学思想方法内化于心. 这样一道例题包罗万象,却又万法归宗.
【教学实施】
师:对于DB,CE你是如何定位的?又如何证明它们相等?
(学生独立思考、探寻证法,教师巡视、捕捉生成性资源)
生27:如图13所示,因为AB=AC,若能证明AD=AE,就可以得到DB=CE. 连接DE,形成圆内接四边形BDEC,得∠B=∠AED,∠C=∠ADE. 根据AB=AC以及等边对等角可得∠B=∠C,再由等量代换推得∠ADE =∠AED,所以AD=AE.
生28:如图14所示,因为AB=AC,所以∠B=∠C,可证=,进一步得=. 由弧等可得弦等,所以DB=CE.
生29:利用三角形全等证明. 如图15所示,连接BE,CD,由BC是直径得∠CDB=∠BEC=90°,结合∠B=∠C和BC=CB,得Rt△BCD≌Rt△CBE,所以BD=CE.
生30:根据圆心角相等可得弦等. 如图16所示,连接OD,OE,得到等腰三角形BOD和等腰三角形COE. 由AB=AC可得∠B=∠C,再根据三角形内角和的性质得圆心角∠BOD=∠COE,所以BD=CE.
生31:如图17所示,过点O作OH⊥AB于H,作OF⊥AC于F. 根据AB=AC,O是BC的中点,易证AO是∠BAC的平分线,于是OH=OF. 以O为圆心、OH为半径作小☉O与AB,AC相切于点H,F,由切线长定理可得AH=AF,于是BH=CF,再根据垂径定理可得2BH=2CF,即BD=CE.
生32:在图17中,也可以先证明Rt△BOH≌Rt△COF,于是BH=CF,再利用垂径定理得到2BH=2CF,即BD=CE.
学科育人导向下问题驱动式单元复习课的实践思考
1. 坚持育人导向,让学习真正发生并经历
学科教学是育人主阵地,作为基础学科的数学,绝不应该仅仅是传递知识的载体,应以其独特的学科特点担负起学科育人的使命. 但长期以来,数学学科具有严谨的逻辑体系和高度的理性精神,部分教师一直以传授知识为目的,甚至理解为培养学生的解题能力,忽视了学生对数学学科完整性的体验,必然不能培养学生良好的数学情怀,导致数学失去了教育价值和育人本质. 在以学科育人为导向的问题驱动式教学理念下,本节课设计了“在圆中画两条弦”的明线主问题,既能引导学生回顾圆的相关知识,又能引领学生经历基本图形的形成过程,感受图形结构的变化,让学生的思维和知识共同成长出来!同时,本节课还埋进了“分类”“转化”以及“特殊与一般”数学思想方法的暗线,学生思维的生长离不开数学思想方法的内化,在数学学习中体悟到数学思想方法,能让学生产生获得感,从而促进学生思维大步成长. 这样的明暗双线在课堂中给学生进行研究活动留足了时间,也给予了学生不同程度的思维发展空间. 这样的每一个学生都能思考的课堂方有一种思维生长的活力和生命成长的张力.
2. 让复习课在循环中不断重设开端
如何创新复习课教学,特别是中考复习课?笔者认为,创新复习课教学就是打破机械重复,需要教师研究教材,智慧整合教学资源,在复习课新一轮次的循环中创新故事的开端,让复习课带给学生“生生不息”的生命成长体验感[2]. 就本节课来说,通过“圆与两条弦的组合构图”的想法给学生一次“重生”的学习体验,而不是刚刚开始就看到结局的乏味. 在“不同以往”的设计中,让学生耳目一新,潜移默化地引导学生面对问题时可以通过不同角度去思考,无形中也渗透了创新能力的培养,这将学生从数学课堂引进了更高更远却很贴近生命成长的地方.
3. 捕捉生成性资源,促动学生思维生长
问题驱动式教学的目的是将教师本位转变成学生本位——以学定教,教师作为问题的提出者、课程的设计者以及结果的评估者,利用问题驱动课堂发展,利用学生即时生成性资源促使课堂生长,建立一种以学生为主体、以专业领域内的各种问题为学习起点、以问题为核心规划学习内容的课堂,使得学生人人能够参与其中,不同的学生获得不同程度的发展. 在这样的课堂中,学生即时生成性资源是串联课堂的关键,教师要及时捕捉这些生成性资源,甄别有效的生成性资源,灵活利用生成性资源,促使课堂高效发展和学生思维快速成长. 在这样的课堂中,教师要多关注师生互动交流、生生互动交流,需要教师充分发挥教学智慧组织引导.
4. 雕刻板书设计,构建知识生长脉络
问题驱动式教学下学生人人有所思考,教师可以利用多媒体呈现不同的生成性资源,这些丰富各异的生成性资源是学生的学习经历,从“指剑乱舞”“思维发散”到建立紧密知识体系的过程需要雕刻一张结构化的板书来让学生摸清知识生长脉络,就好比大家各自将不同的思维板块拼在一起最终组成一幅绝美的画卷,每频回眸,一目芳容收眼底,一览众山万壑生.
参考文献:
[1]中华人民共和国教育部. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[2]卜以楼. 生长型构架下实数复习课的教学实践与思考[J]. 中学数学,2016(06):40-43.
